Главная » В.В. Пасечник » Площадь треугольника по трем высотам. Как найти площадь треугольника. Формулы треугольника. Универсальные способы нахождения площади треугольника

Площадь треугольника по трем высотам. Как найти площадь треугольника. Формулы треугольника. Универсальные способы нахождения площади треугольника

Как вы можете помнить из школьной программы по геометрии, треугольник – это фигура, образованная из трех отрезков, соединяющихся тремя точками, не лежащими на одной прямой. Треугольник образует три угла, отсюда и название фигуры. Определение может быть и иным. Треугольник можно так же назвать многоугольником с тремя углами, ответ будет так же верным. Треугольники делятся по числу равных сторон и по величине углов в фигурах. Так выделяют такие треугольники, как равнобедренный, равносторонний и разносторонний, а так же прямоугольный, остроугольный и тупоугольный, соответственно.

Формул вычисления площади треугольника очень много. Выбирать, как найти площадь треугольника, т.е. какой формулой воспользоваться, только вам. Но стоит отметить лишь некоторые обозначения, которые используются во многих формулах вычисления площади треугольника. Итак, запоминайте:

S – это площадь треугольника,

a, b, c – это стороны треугольника,

h – это высота треугольника,

R – это радиус описанной окружности,

p – это полупериметр.

Вот основные обозначения, которые могут вам пригодиться, если вы совершенно забыли курс геометрии. Ниже будут приведены наиболее понятные и не сложные варианты вычисления неизвестной и загадочной площади треугольника. Это не сложно и пригодится как вам в домашних нуждах, так и для помощи своим детям . Давайте вспомним, как вычислить площадь треугольника проще простого:

В нашем случае площадь треугольника равна: S = ½ * 2,2 см. * 2,5 см. = 2,75 кв.см. Помните, что площадь измеряется в квадратных сантиметрах (кв.см.).

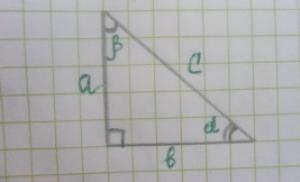
Прямоугольный треугольник и его площадь.

Прямоугольный треугольник – это треугольник, у которого один угол равен 90 градусам (потому называется прямым). Прямой угол образуют две перпендикулярные линии (в случае с треугольником – два перпендикулярных отрезка). В прямоугольном треугольнике прямой угол может быть только один, т.к. сумма всех углов одного любого треугольника равна 180 градусам. Получается, что 2 других угла должны делить между собой оставшиеся 90 градусов, например 70 и 20, 45 и 45 и т.д. Итак, основное вы вспомнили, осталось узнать, как найти площадь прямоугольного треугольника. Представим, что перед нами вот такой прямоугольный треугольник, и нам необходимо найти его площадь S.

1. Самый простой способ определения площади прямоугольного треугольника высчитывается по следующей формуле:

В нашем случае, площадь прямоугольного треугольника равна: S = 2,5 см. * 3 см. / 2 = 3,75 кв.см.

В принципе, больше нет необходимости выверения площади треугольника иными способами, т.к. в быту пригодится и поможет только этот. Но существуют и варианты измерения площади треугольника через острые углы.

2. Для других способов вычисления необходимо иметь таблицу косинусов, синусов и тангенсов. Посудите сами, вот какие варианты вычисления площадей прямоугольного треугольника еще можно использовать:

Мы решили воспользоваться первой формулой и с небольшими помарками (чертили в блокноте и использовали старую линейку и транспортир), но у нас вышел верный расчет:

S = (2,5*2,5)/(2*0,9)=(3*3)/(2*1,2). У нас вышли такие результаты 3,6=3,7, но с учетом сдвига клеток, этот нюанс нам можно простить.

Равнобедренный треугольник и его площадь.

Если перед вами стоит задача вычислить формулу равнобедренного треугольника, то проще всего воспользоваться главной и как считается классической формулой площади треугольника.

Но для начала, перед тем, как найти площадь равнобедренного треугольника, узнаем, что это за фигура такая. Равнобедренным треугольником называется треугольник, у которого две стороны имеют одинаковую длину. Эти две стороны называются боковыми, третья сторона называется основанием. Не путайте равнобедренный треугольник с равносторонним, т.е. правильным треугольником, у которого все три стороны равны. В таком треугольнике нет особых тенденций к углам, точнее к их величине. Однако углы у основания в равнобедренном треугольнике равны, но отличаются от угла между равными сторонами. Итак, первую и главную формулу вы уже знаете, осталось узнать, какие еще формулы определения площади равнобедренного треугольника известны.

Площадь треугольника. Во многих задачах по геометрии связанных с вычислением площадей используются формулы площади треугольника. Их существует несколько, здесь мы рассмотрим основные. Перечислить эти формулы было бы слишком просто и пользы ни какой. Мы разберём происхождение основных формул, тех что используются наиболее чаще.

Перед тем как ознакомиться с выводом формул обязательно посмотрите статью о . После изучения материала вы без труда сможете восстановить формулы в памяти (если вдруг они «вылетят» в нужный вам момент).

Первая формула

Диагональ параллелограмма разбивает его на два равных по площади треугольника:

Следовательно площадь треугольника будет равна половине площади параллелограмма:

Площадь треугольника формула

*То есть если нам будет известна любая сторона треугольника и высота опущенная на эту сторону, то мы всегда сможем вычислить площадь этого треугольника.

Формула вторая

Как уже было изложено в статье о площади параллелограмма формула имеет вид:

Площадь треугольника равна половине его площади, значит :

*То есть если будут известны любые две стороны в треугольнике и угол между ними, мы всегда сможем вычислить площадь такого треугольника.

Формула Герона (третья)

Данную формулу выводить сложно и вам это ни к чему. Посмотрите какая она красивая, можно сказать, что сама запоминается.

*Если даны три стороны треугольника, то по данной формуле мы всегда можем вычислить его площадь.

Формула четвёртая

где r – радиус вписанной окружности

*Если известны три стороны треугольника и радиус вписанной в него окружности, то мы всегда можем найти площадь этого треугольника.

Формула пятая

где R – радиус описанной окружности.

*Если известны три стороны треугольника и радиус описанной около него окружности, то мы всегда можем найти площадь такого треугольника.

Возникает вопрос: если известны три стороны треугольника, то не проще ли его площадь найти по формуле Герона!

Да, бывает проще, но не всегда, иногда возникает сложность. Это связано с извлечением корня. Кроме того, данные формулы очень удобно применять в задачах, где дана площадь треугольника, его стороны и требуется найти радиус вписанной или описанной окружности. Такие задания имеются в составе ЕГЭ.

Давайте отдельно рассмотрим формулу:

Она является частным случаем формулы площади многоугольника, в который вписана окружность:

Рассмотрим её на примере пятиугольника:

Соединим центр окружности с вершинами данного пятиугольника и опустим из центра перпендикуляры к его сторонам. Получим пять треугольников, при чём опущенные перпендикуляры являются радиусами вписанной окружности:

Площадь пятиугольника равна:

Теперь понятно, что если речь идёт о треугольнике, то данная формула приобретает вид:

Формула шестая

Чтобы определить площадь треугольника, можно пользоваться разными формулами. Из всех способов самый легкий и часто применяемый - это умножение высоты на длину основания с последующим делением полученного результата на два. Однако данный метод далеко не единственный. Ниже вы сможете прочесть, как найти площадь треугольника, используя разные формулы.

Отдельно мы рассмотрим способы вычисления площади специфических видов треугольника - прямоугольного, равнобедренного и равностороннего. Каждую формулу мы сопровождаем коротким пояснением, которое поможет вам понять ее суть.

Универсальные способы нахождения площади треугольника

В приведенных ниже формулах используются специальные обозначения. Мы расшифруем каждое из них:

a, b, c – длины трех сторон рассматриваемой нами фигуры;
r – радиус окружности, которая может быть вписана в наш треугольник;
R – радиус той окружности, которая может быть описана вокруг него;
α - величина угла, образованного сторонами b и с;
β - величина угла между a и c;
γ - величина угла, образованного сторонами а и b;
h – высота нашего треугольника, опущенная из угла α на сторону а;
p – половина суммы сторон a, b и с.

Логически понятно, почему можно находить площадь треугольника этим способом. Треугольник легко достраивается до параллелограмма, в котором одна сторона треугольника будет выполнять роль диагонали. Площадь параллелограмма находится умножением длины одной из его сторон на значение высоты, проведенной к ней. Диагональ разделяет этот условный параллелограмм на 2 одинаковых треугольника. Следовательно, совершенно очевидно, что площадь нашего исходного треугольника должна равняться половине площади этого вспомогательного параллелограмма.

S=½ a · b·sin γ

Согласно этой формуле, площадь треугольника находится умножением длин двух его сторон, то есть а и b, на синус образованного ими угла. Эта формула логически выводится из предыдущей. Если опустить высоту из угла β на сторону b, то, согласно свойствам прямоугольного треугольника, при умножении длины стороны a на синус угла γ получаем высоту треугольника, то есть h.

Площадь рассматриваемой фигуры находим путем умножения половины радиуса окружности, которую в него можно вписать, на его периметр. Иными словами, находим произведение полупериметра на радиус упомянутой окружности.

S= a · b · с/4R

Согласно данной формуле, необходимую нам величину можно найти путем деления произведения сторон фигуры на 4 радиуса окружности, вокруг нее описанной.

Эти формулы универсальны, так как дают возможность определить площадь любого треугольника (разностороннего, равнобедренного, равностороннего, прямоугольного). Можно это сделать и при помощи более сложных вычислений, на которых мы подробно останавливаться не станем.

Площади треугольников со специфическими свойствами

Как найти площадь прямоугольного треугольника? Особенностью этой фигуры является то, что две ее стороны одновременно являются ее высотами. Если а и b являются катетами, а с становится гипотенузой, то площадь находим так:

Как найти площадь равнобедренного треугольника? В нем две стороны с длиной а и одна сторона с длиной b. Следовательно, его площадь определить можно путем деления на 2 произведения квадрата стороны а на синус угла γ.

Как найти площадь равностороннего треугольника? В нем длина всех сторон равняется а, а величина всех углов - α. Его высота равна половине произведения длины стороны а на корень квадратный из 3. Чтобы найти площадь правильного треугольника, нужно квадрат стороны а умножить на корень квадратный из 3 и разделить на 4.

Понятие площади

Понятие площади любой геометрической фигуры, в частности треугольника, будем связывать с такой фигурой, как квадрат. За единицу площади любой геометрической фигуры будем принимать площадь квадрата, сторона которого равняется единице. Для полноты, вспомним два основных свойства для понятия площадей геометрических фигур.

Свойство 1: Если геометрические фигуры равны, то значения их площадей также равны.

Свойство 2: Любая фигура может быть разбита на несколько фигур. Причем площадь первоначальной фигуры равняется сумме значений площадей всех составляющих её фигур.

Рассмотрим пример.

Пример 1

Очевидно, что одна из сторон треугольника является диагональю прямоугольника , у которого одна сторона имеет длину $5$ (так как $5$ клеток), а вторая $6$ (так как $6$ клеток). Следовательно, площадь этого треугольника будет равняться половине такого прямоугольника. Площадь прямоугольника равняется

Тогда площадь треугольника равняется

Ответ: $15$.

Далее рассмотрим несколько методов для нахождения площадей треугольников, а именно с помощью высоты и основания, с помощью формулы Герона и площадь равностороннего треугольника.

Как найти площадь треугольника через высоту и основание

Теорема 1

Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.

Математически это выглядит следующим образом

$S=\frac{1}{2}αh$

где $a$ - длина стороны, $h$ - высота, проведенная к ней.

Доказательство.

Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.

Площадь прямоугольника $AXBH$ равняется $h\cdot AH$, а прямоугольника $HBYC$ равняется $h\cdot HC$. Тогда

$S_ABH=\frac{1}{2}h\cdot AH$, $S_CBH=\frac{1}{2}h\cdot HC$

Следовательно, искомая площадь треугольника, по свойству 2, равняется

$S=S_ABH+S_CBH=\frac{1}{2}h\cdot AH+\frac{1}{2}h\cdot HC=\frac{1}{2}h\cdot (AH+HC)=\frac{1}{2}αh$

Теорема доказана.

Пример 2

Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице

Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим

$S=\frac{1}{2}\cdot 9\cdot 9=40,5$

Ответ: $40,5$.

Формула Герона

Теорема 2

Если нам даны три стороны треугольника $α$, $β$ и $γ$, то его площадь можно найти следующим образом

$S=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

здесь $ρ$ означает полупериметр этого треугольника.

Доказательство.

Рассмотрим следующий рисунок:

По теореме Пифагора из треугольника $ABH$ получим

Из треугольника $CBH$, по теореме Пифагора, имеем

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

Из этих двух соотношений получаем равенство

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac{γ^2-α^2+β^2}{2β}$

$h^2=γ^2-(\frac{γ^2-α^2+β^2}{2β})^2$

$h^2=\frac{(α^2-(γ-β)^2)((γ+β)^2-α^2)}{4β^2}$

$h^2=\frac{(α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α)}{4β^2}$

Так как $ρ=\frac{α+β+γ}{2}$, то $α+β+γ=2ρ$, значит

$h^2=\frac{2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α)}{4β^2}$

$h^2=\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2 }$

$h=\sqrt{\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2}}$

$h=\frac{2}{β}\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

По теореме 1, получим

$S=\frac{1}{2} βh=\frac{β}{2}\cdot \frac{2}{β} \sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$

Определение треугольника

Треугольник - это геометрическая фигура, которая образуется в результате пересечения трех отрезков, концы которых не лежат на одной прямой. У любого треугольника есть три стороны, три вершины и три угла.

Онлайн-калькулятор

Треугольники бывают различных видов. Например, существует равносторонний треугольник (тот, у которого все стороны равны), равнобедренный (в нем равны две стороны) и прямоугольный (в котором один из углов прямой, т. е. равен 90 градусам).

Площадь треугольника можно найти различными способами в зависимости от того, какие элементы фигуры известны по условию задачи, будь то углы, длины, либо же вообще радиусы окружностей, связанных с треугольником. Рассмотрим каждый способ отдельно с примерами.

Формула площади треугольника по основанию и высоте

S = 1 2 ⋅ a ⋅ h S= \frac{1}{2}\cdot a\cdot h S = 2 1 ⋅ a ⋅ h ,

A a a - основание треугольника;
h h h - высота треугольника, проведенная к данному основанию a.

Пример

Найти площадь треугольника, если известна длина его основания, равная 10 (см.) и высота, проведенная к этому основанию, равная 5 (см.).

Решение

A = 10 a=10 a = 1 0
h = 5 h=5 h = 5

Подставляем в формулу для площади и получаем:
S = 1 2 ⋅ 10 ⋅ 5 = 25 S=\frac{1}{2}\cdot10\cdot 5=25 S = 2 1 ⋅ 1 0 ⋅ 5 = 2 5 (см. кв.)

Ответ: 25 (см. кв.)

Формула площади треугольника по длинам всех сторон

S = p ⋅ (p − a) ⋅ (p − b) ⋅ (p − c) S= \sqrt{p\cdot(p-a)\cdot (p-b)\cdot (p-c)} S = p ⋅ (p − a ) ⋅ (p − b ) ⋅ (p − c ) ,

A , b , c a, b, c a , b , c - длины сторон треугольника;
p p p - половина суммы всех сторон треугольника (то есть, половина периметра треугольника):

P = 1 2 (a + b + c) p=\frac{1}{2}(a+b+c) p = 2 1 (a + b + c )

Эта формула называется формулой Герона .

Пример

Найти площадь треугольника, если известны длины трех его сторон, равные 3 (см.), 4 (см.), 5 (см.).

Решение

A = 3 a=3 a = 3
b = 4 b=4 b = 4
c = 5 c=5 c = 5

Найдем половину периметра p p p :

P = 1 2 (3 + 4 + 5) = 1 2 ⋅ 12 = 6 p=\frac{1}{2}(3+4+5)=\frac{1}{2}\cdot 12=6 p = 2 1 (3 + 4 + 5 ) = 2 1 ⋅ 1 2 = 6

Тогда, по формуле Герона, площадь треугольника:

S = 6 ⋅ (6 − 3) ⋅ (6 − 4) ⋅ (6 − 5) = 36 = 6 S=\sqrt{6\cdot(6-3)\cdot(6-4)\cdot(6-5)}=\sqrt{36}=6 S = 6 ⋅ (6 − 3 ) ⋅ (6 − 4 ) ⋅ (6 − 5 ) = 3 6 = 6 (см. кв.)

Ответ: 6 (см. кв.)

Формула площади треугольника по одной стороне и двум углам

S = a 2 2 ⋅ sin ⁡ β sin ⁡ γ sin ⁡ (β + γ) S=\frac{a^2}{2}\cdot \frac{\sin{\beta}\sin{\gamma}}{\sin(\beta+\gamma)} S = 2 a 2 ⋅ sin (β + γ ) sin β sin γ ,

A a a - длина стороны треугольника;
β , γ \beta, \gamma β , γ - углы, прилежащие к стороне a a a .

Пример

Дано сторону треугольника, равную 10 (см.) и два прилежащих к ней угла по 30 градусов. Найти площадь треугольника.

Решение

A = 10 a=10 a = 1 0
β = 3 0 ∘ \beta=30^{\circ} β = 3 0 ∘
γ = 3 0 ∘ \gamma=30^{\circ} γ = 3 0 ∘

По формуле:

S = 1 0 2 2 ⋅ sin ⁡ 3 0 ∘ sin ⁡ 3 0 ∘ sin ⁡ (3 0 ∘ + 3 0 ∘) = 50 ⋅ 1 2 3 ≈ 14.4 S=\frac{10^2}{2}\cdot \frac{\sin{30^{\circ}}\sin{30^{\circ}}}{\sin(30^{\circ}+30^{\circ})}=50\cdot\frac{1}{2\sqrt{3}}\approx14.4 S = 2 1 0 2 ⋅ sin (3 0 ∘ + 3 0 ∘ ) sin 3 0 ∘ sin 3 0 ∘ = 5 0 ⋅ 2 3 1 ≈ 1 4 . 4 (см. кв.)