Какую теорему доказал перельман. Cледствие доказательства гипотезы Пуанкаре. Что такое гипотеза Пуанкаре

Три независимых группы математиков утверждают, что полностью доказали гипотезу Пуанкаре — одну из самых сложных задач XX века. Окончательный вердикт, возможно, будет вскоре объявлен на Международном конгрессе математиков.

Процесс доказательства гипотезы Пуанкаре сейчас, по-видимому, вступает в заключительную стадию. Три группы математиков окончательно разобрались в идеях Григория Перельмана и за последние пару месяцев представили свои версии полного доказательства этой гипотезы.

За доказательство гипотезы Пуанкаре присудил премию в миллион долларов, что может показаться удивительным: ведь речь идет об очень частном, малоинтересном факте. На самом деле, для математиков важны не столько свойства трехмерной поверхности, сколько факт трудности самого доказательства. В этой задаче в концентрированном виде сформулировано то, что не удавалось доказать с помощью имевшихся ранее идей и методов геометрии и топологии. Она позволяет как бы заглянуть на уровень глубже, в тот пласт задач, который можно будет решить только с помощью идей «нового поколения».

Фото Н. Четвериковой Последним великим достижением чистой математики называют доказательство петербуржцем Григорием Перельманом в 2002—2003 годах гипотезы Пуанкаре, высказанной в 1904 году и гласящей: «всякое связное, односвязное, компактное трехмерное многообразие без края гомеоморфно сфере S 3 ».

В этой фразе имеется несколько терминов, которые я постараюсь объяснить так, чтобы их общий смысл стал понятен нематематикам (я предполагаю, что читатель закончил среднюю школу и кое-что из школьной математики еще помнит).

Начнем с понятия гомеоморфизма, центрального в топологии. Вообще, топологию часто определяют как «резиновую геометрию», т. е. как науку о свойствах геометрических образов, которые не меняются при плавных деформациях без разрывов и склеек, а точнее, при возможности установить между двумя объектами взаимно-однозначное и взаимно-непрерывное соответствие.

Главную идею проще всего объяснить на классическом примере кружки и бублика. Первую можно превратить во второй непрерывной деформацией: Эти рисунки наглядно показывают, что кружка гомеоморфна бублику, причем этот факт верен как для их поверхностей (двумерных многообразий, называемых тором), так и для заполненных тел (трехмерных многообразий с краем).

Приведем толкование остальных терминов, фигурирующих в формулировке гипотезы.

1. Трехмерное многообразие без края. Это такой геометрический объект, у которого каждая точка имеет окрестность в виде трехмерного шара. Примерами 3-многообразий может служить, во-первых, всё трехмерное пространство, обозначаемое R 3 , а также любые открытые множества точек в R 3 , к примеру внутренность полнотория (бублика). Если рассмотреть замкнутое полно-торие, т. е. добавить и его граничные точки (поверхность тора), то мы получим уже многообразие с краем -у краевых точек нет окрестностей в виде шарика, но лишь в виде половинки шарика.

2. Связное. Понятие связности здесь самое простое. Многообразие связно, если оно состоит из одного куска, или, что-то же самое, любые две его точки можно соединить непрерывной линией, не выходящей за его пределы.

3. Односвязное. Понятие односвязности сложнее. Оно означает, что любую непрерывную замкнутую кривую, расположенную целиком в пределах данного многообразия, можно плавно стянуть в точку, не покидая этого многообразия. Например, обычная двумерная сфера в R 3 односвязна (кольцевую резинку, как угодно приложенную к поверхности яблока, можно плавной деформацией стянуть в одну точку, не отрывая резинки от яблока). С другой стороны, окружность и тор неодносвязны.

4. Компактное. Многообразие компактно, если любой его гомео-морфный образ имеет ограниченные размеры. Например, открытый интервал на прямой (все точки отрезка, кроме его концов) некомпактен, так как его можно непрерывно растянуть до бесконечной прямой. А вот замкнутый отрезок (с концами) является компактным многообразием с краем: при любой непрерывной деформации концы переходят в какие-то определенные точки, и весь отрезок обязан переходить в ограниченную кривую, соединяющую эти точки.

Размерность многообразия -это число степеней свободы у точки, которая на нем «живет». У каждой точки есть окрестность в виде диска соответствующей размерности, т. е. интервала прямой в одномерном случае, круга на плоскости в двумерном, шара в трехмерном и т. д. Одномерных связных многообразий без края с точки зрения топологии всего два: это прямая и окружность. Из них только окружность компактна.

Примером пространства, не являющегося многообразием, может служить, например, пара пересекающихся линий — ведь у точки пересечения двух линий любая окрестность имеет форму креста, у нее нет окрестности, которая была бы сама по себе просто интервалом (а у всех других точек такие окрестности есть). Математики в таких случаях говорят, что мы имеем дело с особым многообразием, у которого есть одна особая точка.

Двумерные компактные многообразия хорошо известны. Если рассматривать только ориентируемые 1 многообразия без края, то они с топологической точки зрения составляют простой, хотя и бесконечный, список: и так далее. Каждое такое многообразие получается из сферы приклеиванием нескольких ручек, число которых называется родом поверхности.

1 За неимением места, я не буду говорить о неориентируемых многообразиях, примером которых может служить известная бутылка Клейна — поверхность, которую нельзя вложить в пространство без самопересечений.

На рисунке изображены поверхности рода 0, 1, 2 и 3. Чем выделяется сфера из всех поверхностей этого списка? Оказывается, односвязностью: на сфере любую замкнутую кривую можно стянуть в точку, а на любой другой поверхности всегда можно указать кривую, которую стянуть в точку по поверхности невозможно.

Любопытно, что и трехмерные компактные многообразия без края можно в некотором смысле классифицировать, т. е. выстроить в некоторый список, хотя не такой прямолинейный, как в двумерном случае, а имеющий довольно сложную структуру. Тем не менее, трехмерная сфера S 3 выделяется в этом списке точно так же, как двумерная сфера в списке, приведенном выше. Тот факт, что любая кривая на S 3 стягивается в точку, доказывается столь же просто, как и в двумерном случае. А вот обратное утверждение, а именно, что это свойство уникально именно для сферы, т. е. что на любом другом трехмерном многообразии есть нестягиваемые кривые, очень трудное и в точности составляет содержание гипотезы Пуанкаре, о которой мы ведем речь.

Важно понимать, что многообразие может жить само по себе, о нем можно мыслить как о независимом объекте, никуда не вложенном. (Представьте себе жизнь двумерных существ на поверхности обычной сферы, не подозревающих о существовании третьего измерения.) К счастью, все двумерные поверхности из приведенного выше списка можно вложить в обычное пространство R 3 , что облегчает их визуализацию. Для трехмерной сферы S 3 (и вообще для любого компактного трехмерного многообразия без края) это уже не так, поэтому необходимы некоторые усилия для того, чтобы понять ее строение.

По-видимому, простейший способ объяснить топологическое устройство трехмерной сферы S 3 — это при помощи одноточечной компактифика-ции. А именно, трехмерная сфера S 3 представляет собой одноточечную компактификацию обычного трехмерного (неограниченного) пространства R 3 .

Поясним эту конструкцию сначала на простых примерах. Возьмем обычную бесконечную прямую (одномерный аналог пространства) и добавим к ней одну «бесконечно удаленную» точку, считая, что при движении по прямой вправо или влево мы в конце концов попадаем в эту точку. С топологической точки зрения нет разницы между бесконечной прямой и ограниченным открытым отрезком (без концевых точек). Такой отрезок можно непрерывно изогнуть в виде дуги, свести поближе концы и вклеить в место стыка недостающую точку. Мы получим, очевидно, окружность — одномерный аналог сферы.

Подобным же образом, если я возьму бесконечную плоскость и добавлю одну точку на бесконечности, к которой стремятся все прямые исходной плоскости, проходимые в любом направлении, то мы получим двумерную (обычную) сферу S 2 . Эту процедуру можно наблюдать при помощи стереографической проекции, которая каждой точке P сферы, за исключением северного полюса N, ставит в соответствие некоторую точку плоскости P":

Таким образом, сфера без одной точки — это топологически все равно, что плоскость, а добавление точки превращает плоскость в сферу.

В принципе, точно такая же конструкция применима и к трехмерной сфере и трехмерному пространству, только для ее осуществления необходим выход в четвертое измерение, и на чертеже это не так просто изобразить. Поэтому я ограничусь словесным описанием одноточечной компактификации пространства R 3 .

Представьте себе, что к нашему физическому пространству (которое мы, вслед за Ньютоном, считаем неограниченным евклидовым пространством с тремя координатами x, y, z) добавлена одна точка «на бесконечности» таким образом, что при движении по прямой в любом направлении вы в нее попадаете (т.е. каждая пространственная прямая замыкается в окружность). Тогда мы получим компактное трехмерное многообразие, которое и есть по определению сфера S 3 .

Легко понять, что сфера S 3 односвязна. В самом деле, любую замкнутую кривую на этой сфере можно немного сдвинуть, чтобы она не проходила через добавленную точку. Тогда мы получим кривую в обычном пространстве R 3 , которая легко стягивается в точку посредством гомотетий, т. е. непрерывного сжатия по всем трем направлениям.

Для понимания, как устроено многообразие S 3 , весьма поучительно рассмотреть его разбиение на два полнотория. Если из пространства R 3 выбросить полноторие, то останется нечто не очень понятное. А если пространство компактифицировать в сферу, то это дополнение превращается тоже в полноторие. То есть сфера S 3 разбивается на два полнотория, имеющих общую границу — тор.

Вот как это можно понять. Вложим тор в R 3 как обычно, в виде круглого бублика, и проведем вертикальную прямую — ось вращения этого бублика. Через ось проведем произвольную плоскость, она пересечет наше полноторие по двум кругам, показанным на рисунке зеленым цветом, а дополнительная часть плоскости разбивается на непрерывное семейство красных окружностей. К их числу относится и центральная ось, выделенная более жирно, потому что в сфере S 3 прямая замыкается в окружность. Трехмерная картина получается из этой двумерной вращением вокруг оси. Полный набор повернутых окружностей заполнит при этом трехмерное тело, гомео-морфное полноторию, только выглядящее необычно.

В самом деле, центральная ось будет в нем осевой окружностью, а остальные будут играть роль параллелей — окружностей, составляющих обычное полноторие.

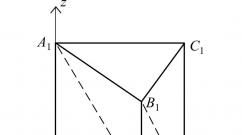
Чтобы было с чем сравнивать 3-сферу, я приведу еще один пример компактного 3-многообразия, а именно трехмерный тор. Трехмерный тор можно построить следующим образом. Возьмем в качестве исходного материала обычный трехмерный куб:

В нем имеется три пары граней: левая и правая, верхняя и нижняя, передняя и задняя. В каждой паре параллельных граней отождествим попарно точки, получающиеся друг из друга переносом вдоль ребра куба. То есть будем считать (чисто абстрактно, без применения физических деформаций), что, например, A и A" - это одна и та же точка, а B и B" - тоже одна точка, но отличная от точки A. Все внутренние точки куба будем рассматривать как обычно. Сам по себе куб-это многообразие с краем, но после проделанных склеек край замыкается сам на себя и исчезает. В самом деле, окрестностями точек A и A" в кубе (они лежат на левой и правой заштрихованных гранях) служат половинки шаров, которые после склейки граней сливаются в целый шарик, служащий окрестностью соответствующей точки трехмерного тора.

Чтобы ощутить устройство 3-тора исходя из обыденных представлений о физическом пространстве, нужно выбрать три взаимно перпендикулярных направления: вперед, влево и вверх — и мысленно считать, как в фантастических рассказах, что при движении в любом из этих направлений достаточно долгое, но конечное время, мы вернемся в исходную точку, но с противоположного направления Это тоже «компактификация пространства», но не одноточечная, использованная раньше для построения сферы, а более сложная.

На трехмерном торе есть нестягиваемые пути; например, таковым является отрезок AA" на рисунке (на торе он изображает замкнутый путь). Его нельзя стянуть, потому что при любой непрерывной деформации точки A и A" обязаны двигаться по своим граням, оставаясь строго друг напротив друга (иначе кривая разомкнется).

Итак, мы видим, что бывают односвязные и неодносвязные компактные 3-многообразия. Перельман доказал, что односвязное многообразие ровно одно.

Исходной идеей доказательства является использование так называемого «потока Риччи»: мы берем односвязное компактное 3-многообразие, наделяем его произвольной геометрией (т.е. вводим некоторую метрику с расстояниями и углами), а затем рассматриваем его эволюцию вдоль потока Риччи. Ричард Гамильтон, который высказал эту идею в 1981 году, надеялся, что при такой эволюции наше многообразие превратится в сферу. Оказалось, что это неверно, — в трехмерном случае поток Риччи способен портить многообразие, т. е. делать из него немногообразие (нечто с особыми точками, как в приведенном выше примере пересекающихся прямых). Перельману путем преодоления неимоверных технических трудностей, с использованием тяжелого аппарата уравнений с частными производными, удалось внести поправки в поток Риччи вблизи особых точек таким образом, что при эволюции топология многообразия не меняется, особых точек не возникает, а в конце концов оно превращается в круглую сферу. Но нужно объяснить наконец, что же такое этот поток Риччи. Потоки, использованные Гамильтоном и Перельманом, относятся к изменению внутренней метрики на абстрактном многообразии, и это объяснить довольно трудно, поэтому я ограничусь описанием «внешнего» потока Риччи на одномерных многообразиях, вложенных в плоскость.

Представим себе гладкую замкнутую кривую на евклидовой плоскости, выберем на ней направление и рассмотрим в каждой точке касательный вектор единичной длины. Тогда при обходе кривой в выбранном направлении этот вектор будет поворачиваться с какой-то угловой скоростью, которая называется кривизной. В тех местах, где кривая изогнута круче, кривизна (по абсолютной величине) будет больше, а там, где она более плавная, кривизна будет меньше.

Кривизну будем считать положительной, если вектор скорости поворачивает в сторону внутренней части плоскости, разбитой нашей кривой на две части, и отрицательной, если он поворачивает вовне. Это соглашение на зависит от направления обхода кривой. В точках перегиба, где вращение меняет направление, кривизна будет равна 0. Например, окружность радиуса 1 имеет постоянную положительную кривизну, равную 1 (если считать ее в радианах).

Теперь забудем про касательные векторы и к каждой точке кривой прикрепим, наоборот, перпендикулярный ей вектор, по длине равный кривизне в данной точке и направленный вовнутрь, если кривизна положительна, и вовне, если отрицательна, а затем заставим каждую точку двигаться в направлении соответствующего вектора со скоростью, пропорциональной его длине. Вот пример:

Оказывается, что любая замкнутая кривая на плоскости ведет себя при такой эволюции подобным же образом, т. е. превращается в конце концов в окружность. Это и есть доказательство одномерного аналога гипотезы Пуанкаре при помощи потока Риччи (впрочем, само утверждение в данном случае и так очевидно, просто способ доказательства иллюстрирует, что происходит в размерности 3).

Заметим в заключение, что рассуждение Перельмана доказывает не только гипотезу Пуанкаре, но и гораздо более общую гипотезу геометризации Тёрстона, которая в известном смысле описывает устройство всех вообще компактных трехмерных многообразий. Но этот предмет лежит уже за рамками настоящей элементарной статьи.

Сергей Дужин,
докт.физ.-мат. наук,
старший научный сотрудник
Санкт-Петербургского отделения
Математического института РАН

Гипотеза Пуанкаре

Гипотеза Пуанкаре́ (точнее Теорема Пуанкаре́ - поскольку это доказанная гипотеза ) является одной из наиболее известных задач топологии. Она даёт достаточное условие того, что пространство является трёхмерной сферой с точностью до деформации.

Формулировка

Гипотеза Пуанкаре

В исходной форме гипотеза Пуанкаре утверждает. Всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере.

Обобщённая гипотеза Пуанкаре.

Обобщённая гипотеза Пуанкаре утверждает: Для любого натурального числа n всякое многообразие размерности n гомотопически эквивалентно сфере размерности n тогда и только тогда, когда оно гомеоморфно ей. Исходная гипотеза Пуанкаре является частным случаем обобщённой гипотезы при n = 3.

История

В 1900 годуПуанкаресделал предположение, что трёхмерное многообразие со всеми группами гомологий как у сферы гомеоморфно сфере. В1904 годуон же нашёл контрпример, называемый теперьсферой Пуанкаре, и сформулировал окончательный вариант своей гипотезы. Попытки доказать гипотезу Пуанкаре привели к многочисленным продвижениям в топологии многообразий.

Гипотеза Пуанкаре долгое время не привлекала интереса. В 1930-х годах Джон Уайтхедвозродил интерес к гипотезе объявив о доказательстве, но затем отказался от него.

Доказательства обобщённой гипотезы Пуанкаре для n ≥ 5 получены в начале 1960-1970-х почти одновременноСмейлом, независимо и другими методамиСтоллингсом(англ. ) (дляn ≥ 7, его доказательство было распространено на случаиn = 5 и 6Зееманом(англ. )). Доказательство значительно более трудного случаяn = 4 было получено только в1982 годуФридманом. Из теоремыНовиковао топологической инвариантности характеристическихклассов Понтрягинаследует, что существуют гомотопически эквивалентные, но не гомеоморфные многообразия в высоких размерностях.

Доказательство исходной гипотезы Пуанкаре (и более общей гипотезы Тёрстона) было найдено только в2002 годуГригорием Перельманом. Впоследствии доказательство Перельмана было проверено и представлено в развёрнутом виде как минимум тремя группами учёных. Доказательство использует модификациюпотока Риччи(так называемыйпоток Риччи с хирургией ) и во многом следует плану, намеченномуГамильтоном, который также первым применил поток Риччи.

Схема доказательства

Поток Риччи - это определённое уравнение в частных производных, похожее на уравнение теплопроводности. Он позволяет деформировать риманову метрику на многообразии, но в процессе деформации возможно образование «сингулярностей» - точек, в которых кривизна стремится к бесконечности, и деформацию невозможно продолжить. Основной шаг в доказательстве состоит в классификации таких сингулярностей в трёхмерном ориентированном случае. При подходе к сингулярности поток останавливают и производят «хирургию» - выбрасывают малую связную компоненту или вырезают «шею» (то есть, открытую областьдиффеоморфную прямому произведению ), а полученные две дырки заклеивают двумя шарами так, что метрика полученного многообразия становится достаточно гладкой - после чего продолжают деформацию вдоль потока Риччи.

Процесс, описанный выше, называется «поток Риччи с хирургией». Классификация сингулярностей позволяет заключить, что каждый «выброшенный кусок» диффеоморфен сферической пространственной форме.

При доказательстве гипотезы Пуанкаре начинают с произвольной римановой метрики на односвязном трёхмерном многообразии и применяют к нему поток Риччи с хирургией. Важным шагом является доказательство того, что в результате такого процесса «выбрасывается» всё. Это означает, что исходное многообразие можно представить как набор сферических пространственных форм , соединённых друг с другом трубками . Подсчёт фундаментальной группы показывает, что диффеоморфно связной сумме набора пространственных форм и более того все тривиальны. Таким образом, является связной суммой набора сфер, то есть сферой.

Григорий Перельман. Отказник

Василий Максимов

В августе 2006 года были объявлены имена лучших математиков планеты, получивших престижнейшую Медаль Филдса – своеобразный аналог Нобелевской премии, которой математики, по прихоти Альфреда Нобеля, были лишены. Премия Fields Medal – помимо почетного знака, лауреатам вручается чек на пятнадцать тысяч канадских долларов – присуждается Международным конгрессом математиков раз в четыре года. Она учреждена канадским ученым Джоном Чарльзом Филдсом и впервые вручена в 1936 году. С 1950 года Fields Medal вручается регулярно лично королем Испании за вклад в развитие математической науки. Лауреатами премии могут стать от одного до четырех ученых в возрасте до сорока лет. Премию уже получили сорок четыре математика, среди которых восемь россиян.

Григорий Перельман. Анри Пуанкаре.

В 2006 году лауреатами стали француз Венделин Вернер, австралиец Теренс Тао и двое россиян – работающий в США Андрей Окуньков и ученый из Петербурга Григорий Перельман. Однако в последний момент стало известно, что Перельман отказался от этой престижной награды – как объявили организаторы, «по принципиальным соображениям».

Столь экстравагантный поступок российского математика не стал неожиданностью для знающих его людей. Он уже не в первый раз отказывается от математических наград, объясняя свое решение тем, что не любит торжественные мероприятия и излишнюю шумиху вокруг своего имени. Еще десять лет назад, в 1996 году, Перельман отказался от премии Европейского математического конгресса, сославшись на то, что не закончил работу над номинированной на награду научной проблемой, и это был не последний случай. Российский математик словно сделал целью своей жизни удивлять людей, идя наперекор общественному мнению и научной общественности.

Григорий Яковлевич Перельман родился 13 июня 1966 года в Ленинграде. С юных лет увлекался точными науками, с блеском окончил знаменитую 239-ю среднюю школу с углубленным изучением математики, побеждал на многочисленных математических олимпиадах: так, в 1982 году в составе команды советских школьников участвовал в Международной математической олимпиаде, проходившей в Будапеште. Перельман без экзаменов был зачислен на мехмат Ленинградского университета, где учился на «отлично», продолжая побеждать в математических соревнованиях всех уровней. Окончив университет с красным дипломом, он поступил в аспирантуру при Петербургском отделении Математического института имени В. А. Стеклова. Его научным руководителем был известный математик академик Александров. Защитив кандидатскую диссертацию, Григорий Перельман остался в институте, в лаборатории геометрии и топологии. Известны его работы по теории пространств Александрова, он сумел найти доказательства к ряду важных гипотез. Несмотря на многочисленные предложения от ведущих западных университетов, Перельман предпочитает работать в России.

Самым громким его успехом стало решение в 2002 году знаменитой гипотезы Пуанкаре, опубликованной в 1904 году и с тех пор остававшейся не доказанной. Перельман работал над нею восемь лет. Гипотеза Пуанкаре считалась одной из величайших математических загадок, а ее решение – важнейшим достижением в математической науке: оно моментально продвинет вперед исследования проблем физико-математических основ мироздания. Виднейшие умы планеты прогнозировали ее решение лишь через несколько десятилетий, а Институт математики Клея в Кембридже, штат Массачусетс, внес проблему Пуанкаре в число семи наиболее интересных нерешенных математических проблем тысячелетия, за решение каждой из которых была обещана премия в миллион долларов (Millennium Prize Problems).

Гипотеза (иногда называемая задачей) французского математика Анри Пуанкаре (1854–1912) формулируется так: любое замкнутое односвязное трехмерное пространство гомеоморфно трехмерной сфере. Для пояснения используют наглядный пример: если обмотать яблоко резиновой лентой, то в принципе, стягивая ленту, можно сжать яблоко в точку. Если же обмотать такой же лентой бублик, то в точку его сжать нельзя без разрыва или бублика, или резины. В таком контексте яблоко называют «односвязной» фигурой, бублик же не односвязен. Почти сто лет назад Пуанкаре установил, что двумерная сфера односвязна, и предположил, что трехмерная сфера тоже односвязна. Доказать эту гипотезу не могли лучшие математики мира.

Чтобы претендовать на приз Института Клея, Перельману нужно было всего лишь опубликовать свое решение в одном из научных журналов, и если в течение двух лет никто не сможет найти ошибку в его вычислениях, то решение будут считать верным. Однако Перельман с самого начала отступил от правил, опубликовав свое решение на сайте препринтов Лос-Аламосской научной лаборатории. Возможно, он опасался того, что в его расчеты вкралась ошибка – подобная история уже происходила в математике. В 1994 году английский математик Эндрю Уайлз предложил решение знаменитой теоремы Ферма, а спустя несколько месяцев выяснилось, что в его расчеты вкралась ошибка (правда, впоследствии она была исправлена, и сенсация всё же состоялась). Официальной публикации доказательства гипотезы Пуанкаре нет до сих пор – зато есть авторитетное мнение лучших математиков планеты, подтверждающих верность расчетов Перельмана.

Медаль Филдса Григорию Перельману была присуждена именно за решение проблемы Пуанкаре. Но российский ученый отказался от премии, которой он без сомнения достоин. «Григорий сказал мне, что чувствует себя изолированным от международного математического сообщества, вне этого сообщества, поэтому не хочет получать награду», – заявил на пресс-конференции в Мадриде президент Всемирного союза математиков (ВСМ) англичанин Джон Болл.

Ходят слухи, что Григорий Перельман и вовсе собирается уйти из науки: еще полгода назад он уволился из родного Математического института имени Стеклова, и говорят, будто он не будет больше заниматься математикой. Возможно, российский ученый считает, что, доказав знаменитую гипотезу, он сделал для науки всё, что мог. А впрочем, кто возьмется рассуждать о ходе мыслей столь яркого ученого и неординарного человека?.. От любых комментариев Перельман отказывается, а газете The Daily Telegraph он заявил: «Ничто из того, что я могу сказать, не представляет ни малейшего общественного интереса». Однако ведущие научные издания были единодушны в своих оценках, когда сообщили, что «Григорий Перельман, разрешив теорему Пуанкаре, встал в один ряд с величайшими гениями прошлого и настоящего».

Ежемесячный литературно-публицистический журнал и издательство.

Анри Пуанкаре (1854-1912), один из величайших математиков, в 1904 г. сформулировал знаменитую идею о деформированной трёхмерной сфере и в виде маленькой заметки на полях, помещённой в конце 65 страничной статьи, посвящённой совершенно другому вопросу, нацарапал несколько строчек довольно странной гипотезы со словами: «Ну этот вопрос может слишком далеко нас завести»…

Маркус Дю Сотой из Оксфордского университета считает, что теорема Пуанкаре — «это центральная проблема математики и физики , попытка понять какой формы может быть Вселенная , к ней очень трудно подобраться».

Раз в неделю Григорий Перельман ездил в Принстон, чтобы принять участие в семинаре «Института углублённых исследований». На семинаре один из математиков Гарвардского университета отвечает на вопрос Перельмана: «Теория Уильяма Тёрстона (1946-2012 гг., математик, труды в области «Трехмерной геометрии и топологии»), получившая название гипотезы геометризации описывает все возможные трёхмерные поверхности и является шагом вперёд по сравнению с гипотезой Пуанкаре. Если Вы докажете предположение Уильяма Тёрстона, то и гипотеза Пуанкаре распахнёт перед Вами все свои двери и более того её решение изменит весь топологический ландшафт современной науки ».

Шесть ведущих американских университетов в марте 2003 г. приглашают Перельмана прочесть цикл лекций, разъясняющих его работу. В апреле 2003 г. Перельман совершает научное турне. Его лекции становятся выдающимся научным событием. В Принстоне послушать его приезжают Джон Болл (председатель международного математического союза), Эндрю Уайлз (математик, работы в области арифметики эллиптических кривых, доказал теорему Ферма в 1994 г.), Джон Нэш (математик, работающий в области теории игр и дифференциальной геометрии).

Григорию Перельману удалось решить одну из семи задач тысячелетия и математически описать так называемою формулу Вселенной , доказать гипотезу Пуанкаре. Над этой гипотезой наиболее светлые умы бились более 100 лет, и за доказательство которой мировым математическим сообществом (математическим институтом имени Клэя) был обещан $1 млн. Её вручение прошло 8 июня 2010 г. Григорий Перельман не появился на ней, и у мирового математического сообщества «поотпадали челюсти».

В 2006 году за решение гипотезы Пуанкаре математику была присуждена высшая математическая награда - Филдсовская премия (медаль Филдса). Джон Болл лично посетил Санкт-Петербург с тем, чтобы уговорить принять премию. Её он принять отказался со словами: «Общество вряд ли способно всерьёз оценить мою работу ».

«Филдсовская премия (и медаль) вручается один раз в 4 года на каждом международном математическом конгрессе молодым учёным (моложе 40 лет), внёсшим заметный вклад в развитие математики. Помимо медали награждённым вручается 15 тыс. канадских долларов ($13 000)»

В исходной формулировке гипотеза Пуанкаре звучит следующим образом: «Всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере». В переводе на общедоступный язык , это означает, что любой трёхмерный объект, например, стакан можно преобразовать в шар путём одной только деформации, то есть его не нужно будет ни разрезать, ни склеивать. Иными словами, Пуанкаре предположил, что пространство не трёхмерно, а содержит значительно большее число измерений , а Перельман спустя 100 лет математически это доказал .

Выражение Григория Перельмана теоремы Пуанкаре о преобразовании материи в другое состояние, форму имеет сходство со знаниями, изложенными в книге Анастасии Новых «Сэнсэй IV»: «По факту, вся эта бесконечная для нас Вселенная занимает место в миллиарды раз меньше, чем кончик самой тонкой медицинской иглы» . А также возможностью управления материальной Вселенной путём преобразований, вносимых Наблюдателем из контролирующих измерений выше шестого (с 7 по 72 включительно) (доклад « » тема «Эзоосмическая решётка»).

Григория Перельмана отличали аскетичность жизни, суровость предъявляемых как себе, так и к другим этических требований. Глядя на него складывается ощущение, что он только телесно проживает в общем со всеми остальными современниками пространстве , а Духовно в каком-то ином , где даже за $1 млн. не идут на самые «невинные» компромиссы с Совестью . И что это за пространство такое, и можно ли хоть краешком глаза посмотреть на него?..

Исключительная важность гипотезы , выдвинутой около века назад математиком Пуанкаре , касается трёхмерных структур и является ключевым элементом современных исследований основ мироздания . Загадка эта, по мнению специалистов института Клэя, одна из семи принципиально важных для развития математики будущего.

Перельман, отвергая медали и премии спрашивает: «А зачем они мне? Они мне совершенно ни к чему. Каждому понятно, если доказательство правильное, то никакого другого признания уже не требуется. Пока во мне не развилась подозрительность, у меня был выбор, либо сказать вслух о дезинтеграции математического сообщества в целом, в связи с его низким моральным уровнем, либо ничего не сказать и позволить обращаться с собой, как с быдлом. Теперь же, когда я стал более чем подозрительным, я не могу оставаться быдлом и продолжать молчать, поэтому мне остаётся только уйти».

Для того чтобы заниматься современной математикой нужно иметь тотально чистый ум, без малейшей примеси, которая дезинтегрирует его, дезориентирует, подменяет ценности, и принять эту премию означает продемонстрировать слабость. Идеальный учёный занимается только наукой, не заботится больше ни о чём (власть и капитал), у него должен быть чистый ум, а для Перельмана нет большей важности, чем жить в соответствии с этим идеалом. Полезно ли для математики вся эта затея с миллионами, и нужен ли настоящему учёному такой стимул? И это желание капитала купить и подчинить себе всё в этом мире разве не оскорбительно? Или можно продать свою чистоту за миллион? Деньги, сколько бы там их ни было, эквивалентны истине Души ? Ведь мы имеем дело с априорной оценкой проблем, к которым деньги просто не должны иметь отношения, разве не так?! Делать же из всего этого что-то вроде лото-миллион, или тотализатор, значит потакать дезинтеграции научного, да и человеческого сообщества в целом (см. доклад и в книге «АллатРа» последние 50 страниц о пути построения созидательного общества). И денежные средства (энергия), которые бизнесмены готовы отдавать на науку, если и надо использовать, то корректно, что ли, не унижая Дух подлинного служения , как ни верти, неоценимого денежным эквивалентом: «Что такое миллион, по сравнению , с чистотой, или Величием тех сфер (об измерениях глобальной Вселенной и о Духовном мире см. книгу «АллатРа» и доклад ) , в которые не способно проникнуть даже человеческое воображение (ум) ?! Что такое миллион звёздного неба для времени?!».

Приведем толкование остальных терминов, фигурирующих в формулировке гипотезы :

- Топология - (от греч. topos - место и logos - учение) - раздел математики, изучающий топологические свойства фигур, т.е. свойства, не изменяющиеся при любых деформациях, производимых без разрывов и склеиваний (точнее, при взаимно однозначных и непрерывных отображениях). Примерами топологических свойств фигур являются размерность, число кривых, ограничивающих данную область, и т.д. Так, окружность, эллипс, контур квадрата имеют одни и те же топологические свойства, т.к. эти линии могут быть деформированы одна в другую описанным выше образом; в то же время кольцо и круг обладают различными топологическими свойствами: круг ограничен одним контуром, а кольцо - двумя.

- Гомеоморфизм (греч. ομοιο - похожий, μορφη - форма) - взаимно однозначное соответствие между двумя топологическим пространствами, при котором оба взаимно обратных отображения, определяемые этим соответствием, непрерывны. Эти отображения называют гомеоморфными, или топологическими отображениями, а также гомеоморфизмами, а о пространствах говорят, что они принадлежат одному топологическому типу называются гомеоморфными, или топологически эквивалентными.

- Трёхмерное многообразие без края . Это такой геометрический объект, у которого каждая точка имеет окрестность в виде трёхмерного шара. Примерами 3-многообразий может служить, во-первых, всё трехмерное пространство, обозначаемое R3 , а также любые открытые множества точек в R3 , к примеру, внутренность полнотория (бублика). Если рассмотреть замкнутое полноторие, т.е. добавить и его граничные точки (поверхность тора), то мы получим уже многообразие с краем - у краевых точек нет окрестностей в виде шарика, но лишь в виде половинки шарика.

- Полното́рие (полното́рий) — геометрическое тело, гомеоморфное произведению двумерного диска и окружности D 2 * S 1 . Неформально, полноторие — бублик, тогда как тор — только его поверхность (пустотелая камера колеса).

- Односвязное . Оно означает, что любую непрерывную замкнутую кривую, расположенную целиком в пределах данного многообразия, можно плавно стянуть в точку, не покидая этого многообразия. Например, обычная двумерная сфера в R3 односвязна (кольцевую резинку, как угодно приложенную к поверхности яблока, можно плавной деформацией стянуть в одну точку, не отрывая резинки от яблока). С другой стороны, окружность и тор неодносвязны.

- Компактное. Многообразие компактно, если любой его гомеоморфный образ имеет ограниченные размеры. Например, открытый интервал на прямой (все точки отрезка, кроме его концов) некомпактен, так как его можно непрерывно растянуть до бесконечной прямой. А вот замкнутый отрезок (с концами) является компактным многообразием с краем: при любой непрерывной деформации концы переходят в какие-то определённые точки, и весь отрезок обязан переходить в ограниченную кривую, соединяющую эти точки.

Ильназ Башаров

Литература:

Доклад «ИСКОННАЯ ФИЗИКА АЛЛАТРА» интернациональной группы учёных Международного общественного движения «АЛЛАТРА» под ред. Анастасии Новых, 2015 г. ;

Новых. А. «АллатРа», К.: АллатРа, 2013 г.