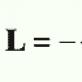Арксинус, арккосинус - свойства, графики, формулы. Обратные тригонометрические функции, их графики и формулы График функции y 2 arcsin x

(круговые функции, аркфункции) — математические функции, которые являются обратными к тригонометрическим функциям .

Арккосинус , обратная функция к cos (x = cos y), y = arccos x определен при и имеет множество значений . Другими словами возвращает угол по значению его cos .

Арккосинус (обозначение: arccos x ; arccos x — это угол , косинус которого равняется x и так далее).

Функция y = cos x непрерывна и ограничена на всей своей числовой прямой. Функция y = arccos x является строго убывающей.

Свойства функции arcsin .

Получение функции arccos .

Дана функция y = cos x . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccos x функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — . На этом отрезке y = cos x строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке существует обратная функция y = arccos x , график которой симметричен графику y = cos x на отрезке относительно прямой y = x .

Функции sin, cos, tg и ctg всегда сопровождаются арксинусом, арккосинусом, арктангенсом и арккотангенсом. Одно является следствием другого, а пары функций одинаково важны для работы с тригонометрическими выражениями.

Рассмотрим рисунок единичной окружности, на котором графически отображено значений тригонометрических функций.

Если вычислить arcs OA, arcos OC, arctg DE и arcctg MK, то все они будут равны значению угла α. Формулы, приведенные ниже, отражают взаимосвязь основных тригонометрических функций и соответствующих им арков.

Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График имеет вид асимметричной кривой, проходящей через центр координат.

Свойства арксинуса:

Если сопоставить графики sin и arcsin , у двух тригонометрических функций можно найти общие закономерности.

Арккосинус

Arccos числа а — это значение угла α, косинус которого равен а.

Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.

Рассмотрим функцию арккосинуса более подробно:

1. Функция определена на отрезке [-1; 1].
2. ОДЗ для arccos — .
3. График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
4. Y = 0 при x = 1.
5. Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.

Некоторые свойства арккосинуса совпадают с функцией косинуса.

Возможно, школьникам покажется излишним такое «подробное» изучение «арков». Однако, в противном случае, некоторые элементарные типовые задания ЕГЭ могут ввести учащихся в тупик.

Задание 1. Укажите функции изображенные на рисунке.

Ответ: рис. 1 – 4, рис.2 — 1.

В данном примере упор сделан на мелочах. Обычно ученики очень невнимательно относятся к построению графиков и внешнему виду функций. Действительно, зачем запоминать вид кривой, если ее всегда можно построить по расчетным точкам. Не стоит забывать, что в условиях теста время, затраченное на рисунок для простого задания, потребуется для решения более сложных заданий.

Арктангенс

Arctg числа a – это такое значение угла α, что его тангенс равен а.

Если рассмотреть график арктангенса, можно выделить следующие свойства:

1. График бесконечен и определен на промежутке (- ∞; + ∞).
2. Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
3. Y = 0 при x = 0.
4. Кривая возрастает на всей области определения.

Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.

Арккотангенс

Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.

Свойства функции арккотангенса:

1. Интервал определения функции – бесконечность.
2. Область допустимых значений – промежуток (0; π).
3. F(x) не является ни четной, ни нечетной.
4. На всем своем протяжении график функции убывает.

Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.

Задание 2. Соотнести график и форму записи функции.

Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,

Ответ: рис. 1 – 1, рис. 2 – 4.

Тригонометрические тождества arcsin, arcos, arctg и arcctg

Ранее нами уже была выявлена взаимосвязь между арками и основными функциями тригонометрии. Данная зависимость может быть выражена рядом формул, позволяющих выразить, например, синус аргумента, через его арксинус, арккосинус или наоборот. Знание подобных тождеств бывает полезным при решении конкретных примеров.

Также существуют соотношения для arctg и arcctg:

Еще одна полезная пара формул, устанавливает значение для суммы значений arcsin и arcos, а также arcctg и arcctg одного и того же угла.

Примеры решения задач

Задания по тригонометрии можно условно разделить на четыре группы: вычислить числовое значение конкретного выражения, построить график данной функции, найти ее область определения или ОДЗ и выполнить аналитические преображения для решения примера.

При решении первого типа задач необходимо придерживаться следующего плана действий:

При работе с графиками функций главное – это знание их свойств и внешнего вида кривой. Для решения тригонометрических уравнений и неравенств необходимы таблицы тождеств. Чем больше формул помнит школьник, тем проще найти ответ задания.

Допустим в ЕГЭ необходимо найти ответ для уравнения типа:

Если правильно преобразовать выражение и привести к нужному виду, то решить его очень просто и быстро. Для начала, перенесем arcsin x в правую часть равенства.

Если вспомнить формулу arcsin (sin α) = α , то можно свести поиск ответов к решению системы из двух уравнений:

Ограничение на модель x возникло, опять таки из свойств arcsin: ОДЗ для x [-1; 1]. При а ≠0, часть сиcтемы представляет собой квадратное уравнение с корнями x1 = 1 и x2 = — 1/a. При a = 0, x будет равен 1.

Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin x , при заданном , имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны . Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin x . Если ограничить аргумент x интервалом , то на нем функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y .

Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.

Арксинус (y = arcsin x ) - это функция, обратная к синусу (x = sin y
Арккосинус (y = arccos x ) - это функция, обратная к косинусу (x = cos y ), имеющая область определения и множество значений .
Арктангенс (y = arctg x ) - это функция, обратная к тангенсу (x = tg y ), имеющая область определения и множество значений .
Арккотангенс (y = arcctg x ) - это функция, обратная к котангенсу (x = ctg y ), имеющая область определения и множество значений .

Графики обратных тригонометрических функций

Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x . См. разделы Синус, косинус , Тангенс, котангенс .

y = arcsin x

y = arccos x

y = arctg x

y = arcctg x

Основные формулы

Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.

arcsin(sin x) = x при
sin(arcsin x) = x
arccos(cos x) = x при
cos(arccos x) = x

arctg(tg x) = x при
tg(arctg x) = x
arcctg(ctg x) = x при
ctg(arcctg x) = x

Формулы, связывающие обратные тригонометрические функции

См. также: Вывод формул обратных тригонометрических функций

Формулы суммы и разности

при или

при и

при и

при или

при и

при и

при

при

при

при

при

при

при

при

при

при

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Определение и обозначения

Арксинус (y = arcsin x ) - это функция, обратная к синусу (x = sin y -1 ≤ x ≤ 1 и множество значений -π/2 ≤ y ≤ π/2 .
sin(arcsin x) = x ;
arcsin(sin x) = x .

Арксинус иногда обозначают так:
.

График функции арксинус

График функции y = arcsin x

График арксинуса получается из графика синуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арксинуса.

Арккосинус, arccos

Определение и обозначения

Арккосинус (y = arccos x ) - это функция, обратная к косинусу (x = cos y ). Он имеет область определения -1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π .
cos(arccos x) = x ;
arccos(cos x) = x .

Арккосинус иногда обозначают так:
.

График функции арккосинус

График функции y = arccos x

График арккосинуса получается из графика косинуса, если поменять местами оси абсцисс и ординат. Чтобы устранить многозначность, область значений ограничивают интервалом , на котором функция монотонна. Такое определение называют главным значением арккосинуса.

Четность

Функция арксинус является нечетной:
arcsin(- x) = arcsin(-sin arcsin x) = arcsin(sin(-arcsin x)) = - arcsin x

Функция арккосинус не является четной или нечетной:
arccos(- x) = arccos(-cos arccos x) = arccos(cos(π-arccos x)) = π - arccos x ≠ ± arccos x

Свойства - экстремумы, возрастание, убывание

Функции арксинус и арккосинус непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства арксинуса и арккосинуса представлены в таблице.

	y = arcsin x	y = arccos x
Область определения и непрерывность	- 1 ≤ x ≤ 1	- 1 ≤ x ≤ 1
Область значений
Возрастание, убывание	монотонно возрастает	монотонно убывает
Максимумы
Минимумы
Нули, y = 0	x = 0	x = 1
Точки пересечения с осью ординат, x = 0	y = 0	y = π/2

Таблица арксинусов и арккосинусов

В данной таблице представлены значения арксинусов и арккосинусов, в градусах и радианах, при некоторых значениях аргумента.

x	arcsin x		arccos x
	град.	рад.	град.	рад.
- 1	- 90°	-	180°	π
-	- 60°	-	150°
-	- 45°	-	135°
-	- 30°	-	120°
0	0°	0	90°
	30°		60°
	45°		45°
	60°		30°
1	90°		0°	0

≈ 0,7071067811865476
≈ 0,8660254037844386

Формулы

См. также: Вывод формул обратных тригонометрических функций

Формулы суммы и разности

при или

при и

при и

при или

при и

при и

при

при

при

при

Выражения через логарифм, комплексные числа

См. также: Вывод формул

Выражения через гиперболические функции

Производные

;
.
См. Вывод производных арксинуса и арккосинуса > > >

Производные высших порядков :
,
где - многочлен степени . Он определяется по формулам:
;
;
.

См. Вывод производных высших порядков арксинуса и арккосинуса > > >

Интегралы

Делаем подстановку x = sin t . Интегрируем по частям, учитывая что -π/2 ≤ t ≤ π/2 , cos t ≥ 0 :
.

Выразим арккосинус через арксинус:
.

Разложение в ряд

При |x| < 1 имеет место следующее разложение:
;
.

Обратные функции

Обратными к арксинусу и арккосинусу являются синус и косинус , соответственно.

Следующие формулы справедливы на всей области определения:
sin(arcsin x) = x
cos(arccos x) = x .

Следующие формулы справедливы только на множестве значений арксинуса и арккосинуса:
arcsin(sin x) = x при
arccos(cos x) = x при .

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

См. также: