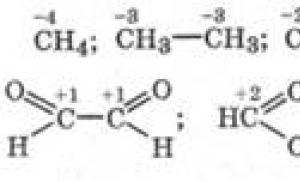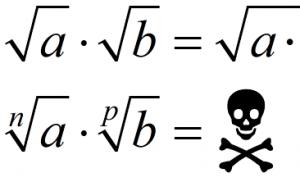Rădăcină pătrată. Acțiuni cu rădăcini pătrate. Modul. Comparația rădăcinilor pătrate. Adunarea și scăderea rădăcinilor, exemple

Bună pisicuțe! Ultima dată am analizat în detaliu ce sunt rădăcinile (dacă nu vă amintiți, vă recomand să citiți). Concluzia principală a acelei lecții: există o singură definiție universală a rădăcinilor, pe care trebuie să o cunoașteți. Restul sunt o prostie și o pierdere de timp.

Astăzi mergem mai departe. Vom învăța să înmulțim rădăcini, vom studia câteva probleme asociate înmulțirii (dacă aceste probleme nu sunt rezolvate, atunci pot deveni fatale la examen) și vom exersa corespunzător. Așa că aprovizionați-vă cu floricele de porumb, faceți-vă confortabil - și vom începe. :)

Încă nu ai fumat, nu-i așa?

Lecția s-a dovedit a fi destul de mare, așa că am împărțit-o în două părți:

1. În primul rând, ne vom uita la regulile de înmulțire. Capul pare să sugereze: atunci când există două rădăcini, există un semn „multiplicare” între ele - și vrem să facem ceva cu el.
2. Apoi vom analiza situația inversă: există o rădăcină mare și am fost nerăbdători să o prezentăm ca un produs a două rădăcini într-un mod mai simplu. Cu ce ​​frică este necesară este o întrebare separată. Vom analiza doar algoritmul.

Pentru cei care abia așteaptă să intre direct în partea 2, sunteți bineveniți. Să începem cu restul în ordine.

Regula de bază a înmulțirii

Să începem cu cele mai simple - rădăcini pătrate clasice. Cele care sunt notate cu $\sqrt(a)$ și $\sqrt(b)$. Pentru ei, totul este în general clar:

regula înmulțirii. Pentru a înmulți o rădăcină pătrată cu alta, trebuie doar să înmulțiți expresiile radicale ale acestora și să scrieți rezultatul sub radicalul comun:

\[\sqrt(a)\cdot \sqrt(b)=\sqrt(a\cdot b)\]

Nu se impun restricții suplimentare pentru numerele din dreapta sau din stânga: dacă există rădăcini multiplicatoare, atunci există și produsul.

Exemple. Luați în considerare patru exemple cu numere simultan:

\[\begin(align) & \sqrt(25)\cdot \sqrt(4)=\sqrt(25\cdot 4)=\sqrt(100)=10; \\ & \sqrt(32)\cdot \sqrt(2)=\sqrt(32\cdot 2)=\sqrt(64)=8; \\ & \sqrt(54)\cdot \sqrt(6)=\sqrt(54\cdot 6)=\sqrt(324)=18; \\ & \sqrt(\frac(3)(17))\cdot \sqrt(\frac(17)(27))=\sqrt(\frac(3)(17)\cdot \frac(17)(27) ))=\sqrt(\frac(1)(9))=\frac(1)(3). \\ \end(align)\]

După cum puteți vedea, sensul principal al acestei reguli este de a simplifica expresiile iraționale. Și dacă în primul exemplu am fi extras rădăcinile din 25 și 4 fără reguli noi, atunci staniul începe: $\sqrt(32)$ și $\sqrt(2)$ nu se numără de la sine, ci produsul lor se dovedește a fi un pătrat exact, deci rădăcina lui este egală cu un număr rațional.

Separat, aș dori să notez ultimul rând. Acolo, ambele expresii radicale sunt fracții. Datorită produsului, mulți factori se anulează, iar întreaga expresie se transformă într-un număr adecvat.

Desigur, nu totul va fi întotdeauna atât de frumos. Uneori, sub rădăcini vor fi prostii complete - nu este clar ce să faci cu ea și cum să se transforme după înmulțire. Puțin mai târziu, când începi să studiezi ecuațiile și inegalitățile iraționale, vor exista tot felul de variabile și funcții în general. Și de foarte multe ori, compilatorii problemelor contează doar pe faptul că veți găsi niște termeni sau factori de contractare, după care sarcina va fi mult simplificată.

În plus, nu este necesar să se înmulțească exact două rădăcini. Puteți înmulți trei deodată, patru - da chiar și zece! Acest lucru nu va schimba regula. Aruncă o privire:

\[\begin(align) & \sqrt(2)\cdot \sqrt(3)\cdot \sqrt(6)=\sqrt(2\cdot 3\cdot 6)=\sqrt(36)=6; \\ & \sqrt(5)\cdot \sqrt(2)\cdot \sqrt(0,001)=\sqrt(5\cdot 2\cdot 0,001)= \\ & =\sqrt(10\cdot \frac(1) (1000))=\sqrt(\frac(1)(100))=\frac(1)(10). \\ \end(align)\]

Și din nou o mică remarcă asupra celui de-al doilea exemplu. După cum puteți vedea, în al treilea multiplicator, există o fracție zecimală sub rădăcină - în procesul de calcule, o înlocuim cu una obișnuită, după care totul este ușor de redus. Deci: vă recomand cu căldură să scăpați de fracțiile zecimale din orice expresii iraționale (adică care conțin cel puțin o pictogramă radicală). Acest lucru vă va economisi mult timp și nervi în viitor.

Dar a fost o digresiune lirică. Acum să luăm în considerare un caz mai general - când exponentul rădăcină conține un număr arbitrar $n$, și nu doar cei doi „clasici”.

Cazul unui indicator arbitrar

Deci, ne-am dat seama de rădăcinile pătrate. Și ce să faci cu cuburile? Sau, în general, cu rădăcini de grad arbitrar $n$? Da, totul este la fel. Regula rămâne aceeași:

Pentru a înmulți două rădăcini de grad $n$, este suficient să înmulțim expresiile lor radicale, după care rezultatul se scrie sub un radical.

In general, nimic complicat. Cu excepția cazului în care volumul calculelor poate fi mai mare. Să ne uităm la câteva exemple:

Exemple. Calculați produsele:

\[\begin(align) & \sqrt(20)\cdot \sqrt(\frac(125)(4))=\sqrt(20\cdot \frac(125)(4))=\sqrt(625)= 5; \\ & \sqrt(\frac(16)(625))\cdot \sqrt(0,16)=\sqrt(\frac(16)(625)\cdot \frac(16)(100))=\sqrt (\frac(64)(((25)^(2))\cdot 25))= \\ & =\sqrt(\frac(((4)^(3)))(((25)^(3 ))))=\sqrt(((\left(\frac(4)(25) \right))^(3)))=\frac(4)(25). \\ \end(align)\]

Și din nou atenție la a doua expresie. Înmulțim rădăcinile cubice, scăpăm de fracția zecimală și, ca rezultat, obținem produsul numerelor 625 și 25 la numitor. Acesta este un număr destul de mare - personal, nu voi calcula imediat ce este egal. la.

Prin urmare, am selectat pur și simplu cubul exact în numărător și numitor și apoi am folosit una dintre proprietățile cheie (sau, dacă doriți, definiția) rădăcinii gradului $n$:

\[\begin(align) & \sqrt(((a)^(2n+1)))=a; \\ & \sqrt(((a)^(2n)))=\left| a\dreapta|. \\ \end(align)\]

Astfel de „escrocherii” vă pot economisi mult timp la un examen sau un test, așa că rețineți:

Nu vă grăbiți să înmulțiți numerele din expresia radicală. În primul rând, verificați: ce se întâmplă dacă gradul exact al oricărei expresii este „criptat” acolo?

Cu toată evidenta acestei remarci, trebuie să recunosc că majoritatea studenților nepregătiți nu văd exact gradele. În schimb, înmulțesc totul înainte și apoi se întreabă: de ce au obținut numere atât de brutale? :)

Totuși, toate acestea sunt o joacă de copii în comparație cu ceea ce vom studia acum.

Înmulțirea rădăcinilor cu exponenți diferiți

Ei bine, acum putem înmulți rădăcini cu aceiași exponenți. Ce se întâmplă dacă scorurile sunt diferite? Spune, cum înmulți un $\sqrt(2)$ obișnuit cu niște prostii ca $\sqrt(23)$? Este chiar posibil să faci asta?

Da, sigur că poți. Totul se face după această formulă:

Regula înmulțirii rădăcinilor. Pentru a înmulți $\sqrt[n](a)$ cu $\sqrt[p](b)$, faceți următoarea transformare:

\[\sqrt[n](a)\cdot \sqrt[p](b)=\sqrt(((a)^(p))\cdot ((b)^(n)))\]

Cu toate acestea, această formulă funcționează numai dacă expresiile radicale sunt nenegative. Aceasta este o remarcă foarte importantă, la care vom reveni puțin mai târziu.

Deocamdată, să ne uităm la câteva exemple:

\[\begin(align) & \sqrt(3)\cdot \sqrt(2)=\sqrt(((3)^(4))\cdot ((2)^(3)))=\sqrt(81) \cdot8)=\sqrt(648); \\ & \sqrt(2)\cdot \sqrt(7)=\sqrt(((2)^(5))\cdot ((7)^(2)))=\sqrt(32\cdot 49)= \sqrt(1568); \\ & \sqrt(5)\cdot \sqrt(3)=\sqrt(((5)^(4))\cdot ((3)^(2)))=\sqrt(625\cdot 9)= \sqrt(5625). \\ \end(align)\]

După cum puteți vedea, nimic complicat. Acum să ne dăm seama de unde a venit cerința de non-negativitate și ce se va întâmpla dacă o încălcăm. :)

Este ușor să înmulți rădăcinile.

De ce expresiile radicale trebuie să fie nenegative?

Desigur, puteți deveni ca profesorii de școală și puteți cita un manual cu un aspect inteligent:

Cerința de non-negativitate este asociată cu diferite definiții ale rădăcinilor de grade pare și impare (respectiv, domeniile lor de definiție sunt și ele diferite).

Ei bine, a devenit mai clar? Personal, când am citit această prostie în clasa a VIII-a, am înțeles pentru mine ceva de genul: „Cerința de non-negativitate este asociată cu *#&^@(*#@^#)~%” - pe scurt, eu nu am inteles nimic la vremea aia. :)

Așa că acum voi explica totul într-un mod normal.

Mai întâi, să aflăm de unde vine formula de înmulțire de mai sus. Pentru a face acest lucru, permiteți-mi să vă reamintesc o proprietate importantă a rădăcinii:

\[\sqrt[n](a)=\sqrt(((a)^(k)))\]

Cu alte cuvinte, putem ridica în siguranță expresia rădăcinii la orice putere naturală $k$ - în acest caz, indicele rădăcinii va trebui înmulțit cu aceeași putere. Prin urmare, putem reduce cu ușurință orice rădăcină la un indicator comun, după care ne înmulțim. De aici provine formula de înmulțire:

\[\sqrt[n](a)\cdot \sqrt[p](b)=\sqrt(((a)^(p)))\cdot \sqrt(((b)^(n)))= \sqrt(((a)^(p))\cdot ((b)^(n)))\]

Dar există o problemă care limitează sever aplicarea tuturor acestor formule. Luați în considerare acest număr:

Conform formulei tocmai oferite, putem adăuga orice grad. Să încercăm să adăugăm $k=2$:

\[\sqrt(-5)=\sqrt(((\left(-5 \right))^(2)))=\sqrt(((5)^(2)))\]

Am eliminat minusul tocmai pentru că pătratul arde minusul (ca orice alt grad par). Și acum să facem transformarea inversă: „reducem” cele două în exponent și grad. La urma urmei, orice egalitate poate fi citită atât de la stânga la dreapta, cât și de la dreapta la stânga:

\[\begin(align) & \sqrt[n](a)=\sqrt(((a)^(k)))\Rightarrow \sqrt(((a)^(k)))=\sqrt[n ](A); \\ & \sqrt(((a)^(k)))=\sqrt[n](a)\Rightarrow \sqrt((((5)^(2)))=\sqrt(((5)^( 2)))=\sqrt(5). \\ \end(align)\]

Dar apoi se întâmplă ceva nebunesc:

\[\sqrt(-5)=\sqrt(5)\]

Acest lucru nu se poate datora faptului că $\sqrt(-5) \lt 0$ și $\sqrt(5) \gt 0$. Aceasta înseamnă că pentru puteri par și numere negative, formula noastră nu mai funcționează. După care avem două opțiuni:

1. A lupta împotriva zidului pentru a afirma că matematica este o știință stupidă, unde „există niște reguli, dar acest lucru este inexact”;
2. Introduceți restricții suplimentare în baza cărora formula va deveni 100% funcțională.

În prima opțiune, va trebui să prindem în mod constant cazuri „nefuncționale” - acest lucru este dificil, lung și, în general, fu. Prin urmare, matematicienii au preferat a doua opțiune. :)

Dar nu-ți face griji! În practică, această restricție nu afectează în niciun fel calculele, deoarece toate problemele descrise se referă doar la rădăcinile unui grad impar, iar minusurile pot fi scoase din ele.

Prin urmare, formulăm o altă regulă care se aplică în general tuturor acțiunilor cu rădăcini:

Înainte de a multiplica rădăcinile, asigurați-vă că expresiile radicale nu sunt negative.

Exemplu. În numărul $\sqrt(-5)$, puteți scoate minusul de sub semnul rădăcină - atunci totul va fi bine:

\[\begin(align) & \sqrt(-5)=-\sqrt(5) \lt 0\Rightarrow \\ & \sqrt(-5)=-\sqrt((((5)^(2))) =-\sqrt(25)=-\sqrt(((5)^(2)))=-\sqrt(5) \lt 0 \\ \end(align)\]

Simte diferenta? Dacă lăsați un minus sub rădăcină, atunci când expresia radicală este pătrată, va dispărea și va începe prostiile. Și dacă scoți mai întâi un minus, atunci poți chiar să ridici/elimini un pătrat până când vei fi albastru în față - numărul va rămâne negativ. :)

Astfel, cel mai corect și mai fiabil mod de a multiplica rădăcinile este următorul:

1. Eliminați toate minusurile de sub radicali. Minusurile sunt doar în rădăcinile multiplicității impare - pot fi plasate în fața rădăcinii și, dacă este necesar, reduse (de exemplu, dacă există două dintre aceste minusuri).
2. Efectuați înmulțirea conform regulilor discutate mai sus în lecția de astăzi. Dacă indicii rădăcinilor sunt aceiași, pur și simplu înmulțiți expresiile rădăcinilor. Și dacă sunt diferite, folosim formula rea ​​\[\sqrt[n](a)\cdot \sqrt[p](b)=\sqrt(((a)^(p))\cdot ((b) ^(n) ))\].
3. 3. Ne bucurăm de rezultat și de notele bune. :)

Bine? Să exersăm?

Exemplul 1. Simplificați expresia:

\[\begin(align) & \sqrt(48)\cdot \sqrt(-\frac(4)(3))=\sqrt(48)\cdot \left(-\sqrt(\frac(4)(3) )) \right)=-\sqrt(48)\cdot \sqrt(\frac(4)(3))= \\ & =-\sqrt(48\cdot \frac(4)(3))=-\ sqrt(64)=-4; \end(align)\]

Aceasta este cea mai simplă opțiune: indicatorii rădăcinilor sunt aceiași și ciudați, problema este doar în minusul celui de-al doilea multiplicator. Îndurăm acest minus nafig, după care totul este ușor de luat în considerare.

Exemplul 2. Simplificați expresia:

\[\begin(align) & \sqrt(32)\cdot \sqrt(4)=\sqrt(((2)^(5)))\cdot \sqrt(((2)^(2)))= \sqrt(((\left(((2)^(5)) \right))^(3))\cdot ((\left(((2)^(2)) \right))^(4) ))= \\ & =\sqrt(((2)^(15))\cdot ((2)^(8)))=\sqrt(((2)^(23))) \\ \end( alinia)\]

Aici, mulți ar fi confuzi de faptul că rezultatul s-a dovedit a fi un număr irațional. Da, se întâmplă: nu am putut scăpa complet de rădăcină, dar cel puțin am simplificat semnificativ expresia.

Exemplul 3. Simplificați expresia:

\[\begin(align) & \sqrt(a)\cdot \sqrt(((a)^(4)))=\sqrt(((a)^(3))\cdot ((\left((() a)^(4)) \right))^(6)))=\sqrt(((a)^(3))\cdot ((a)^(24)))= \\ & =\sqrt( ((a)^(27)))=\sqrt(((a)^(3\cdot 9)))=\sqrt(((a)^(3))) \end(align)\]

Acesta este ceea ce aș dori să vă atrag atenția. Există două puncte aici:

1. Sub rădăcină nu se află un anumit număr sau grad, ci variabila $a$. La prima vedere, acest lucru este puțin neobișnuit, dar în realitate, atunci când rezolvați probleme matematice, cel mai adesea va trebui să vă ocupați de variabile.
2. În final, am reușit să „reducem” exponentul rădăcină și gradul în expresia radicală. Acest lucru se întâmplă destul de des. Și asta înseamnă că a fost posibil să simplificați semnificativ calculele dacă nu utilizați formula principală.

De exemplu, puteți face acest lucru:

\[\begin(align) & \sqrt(a)\cdot \sqrt(((a)^(4)))=\sqrt(a)\cdot \sqrt(((\left(((a))^( 4)) \right))^(2)))=\sqrt(a)\cdot \sqrt(((a)^(8))) \\ & =\sqrt(a\cdot ((a)^( 8)))=\sqrt(((a)^(9)))=\sqrt(((a)^(3\cdot 3)))=\sqrt(((a)^(3))) \ \ \end(align)\]

De fapt, toate transformările au fost efectuate numai cu al doilea radical. Și dacă nu pictați în detaliu toți pașii intermediari, atunci în cele din urmă cantitatea de calcule va scădea semnificativ.

De fapt, am întâlnit deja o sarcină similară mai sus când am rezolvat exemplul $\sqrt(5)\cdot \sqrt(3)$. Acum se poate scrie mult mai ușor:

\[\begin(align) & \sqrt(5)\cdot \sqrt(3)=\sqrt(((5)^(4))\cdot ((3)^(2)))=\sqrt(( (\left((((5)^(2))\cdot 3 \right))^(2)))= \\ & =\sqrt(((\left(75 \right))^(2))) =\sqrt(75). \end(align)\]

Ei bine, ne-am dat seama de înmulțirea rădăcinilor. Acum luați în considerare operația inversă: ce să faceți când există o lucrare sub rădăcină?

În matematică, orice acțiune are propria ei pereche-opus - în esență, aceasta este una dintre manifestările legii hegeliene a dialecticii: „unitatea și lupta contrariilor”. Una dintre acțiunile dintr-o astfel de „pereche” vizează creșterea numărului, iar cealaltă, opusă acesteia, este în scădere. De exemplu, acțiunea opusă adunării este scăderea, iar împărțirea corespunde înmulțirii. Ridicarea la putere are, de asemenea, o pereche dialectică proprie. Este vorba despre extragerea rădăcinilor.

A extrage rădăcina unui astfel de grad dintr-un număr înseamnă a calcula ce număr trebuie ridicat la puterea corespunzătoare pentru a ajunge la acest număr. Cele două grade au propriile nume separate: al doilea grad se numește „pătrat”, iar al treilea - „cubul”. Prin urmare, este plăcut să numim rădăcinile acestor puteri rădăcină pătrată și rădăcină cubică. Acțiunile cu rădăcini cubice sunt un subiect pentru o discuție separată, dar acum să vorbim despre adăugarea rădăcinilor pătrate.

Să începem cu faptul că în unele cazuri este mai ușor să extragi mai întâi rădăcini pătrate, apoi să adăugăm rezultatele. Să presupunem că trebuie să găsim valoarea unei astfel de expresii:

La urma urmei, nu este deloc dificil să calculezi că rădăcina pătrată a lui 16 este 4 și a lui 121 - 11. Prin urmare,

√16+√121=4+11=15

Cu toate acestea, acesta este cel mai simplu caz - aici vorbim de pătrate pline, adică. despre numere care se obțin prin pătrarea numerelor întregi. Dar acest lucru nu este întotdeauna cazul. De exemplu, numărul 24 nu este un pătrat perfect (nu puteți găsi un număr întreg care, atunci când este ridicat la a doua putere, ar avea ca rezultat 24). Același lucru este valabil și pentru un număr ca 54... Ce se întâmplă dacă trebuie să adunăm rădăcinile pătrate ale acestor numere?

În acest caz, vom obține în răspuns nu un număr, ci o altă expresie. Maximul pe care îl putem face aici este să simplificăm cât mai mult expresia originală. Pentru a face acest lucru, va trebui să eliminați factorii de sub rădăcina pătrată. Să vedem cum se face acest lucru folosind numerele menționate ca exemplu:

Pentru început, să factorizăm 24 - în așa fel încât unul dintre ei să poată fi luat cu ușurință ca rădăcină pătrată (adică, astfel încât să fie un pătrat perfect). Există un astfel de număr - acesta este 4:

Acum să facem același lucru cu 54. În compoziția sa, acest număr va fi 9:

Astfel, obținem următoarele:

√24+√54=√(4*6)+ √(9*6)

Acum să extragem rădăcinile din ceea ce le putem extrage: 2*√6+3*√6

Există un factor comun aici, pe care îl putem scoate din paranteze:

(2+3)* √6=5*√6

Acesta va fi rezultatul adăugării - nimic altceva nu poate fi extras aici.

Adevărat, puteți recurge la ajutorul unui calculator - totuși, rezultatul va fi aproximativ și cu un număr mare de zecimale:

√6=2,449489742783178

Rotunjind-o treptat, obținem aproximativ 2,5. Dacă totuși am dori să aducem soluția exemplului anterior la concluzia sa logică, putem înmulți acest rezultat cu 5 - și obținem 12,5. Un rezultat mai precis cu astfel de date inițiale nu poate fi obținut.

Atenţie!
Există suplimentare
material în secțiunea specială 555.
Pentru cei puternici „nu foarte. »
Și pentru cei care „foarte chiar. "")

În lecția anterioară, ne-am dat seama ce este o rădăcină pătrată. Este timpul să ne dăm seama care sunt formule pentru rădăcini, ce sunt proprietățile rădăciniiși ce se poate face cu toate acestea.

Formule rădăcină, proprietăți rădăcină și reguli pentru acțiunile cu rădăcini sunt în esență același lucru. Există surprinzător de puține formule pentru rădăcini pătrate. Ceea ce, desigur, mulțumește! Mai degrabă, puteți scrie o mulțime de tot felul de formule, dar doar trei sunt suficiente pentru o muncă practică și sigură cu rădăcini. Orice altceva decurge din acești trei. Deși mulți se rătăcesc în cele trei formule ale rădăcinilor, da.

Să începem cu cel mai simplu. Iat-o:

Vă reamintesc (din lecția anterioară): a și b sunt numere nenegative! Altfel, formula nu are sens.

Această proprietate a rădăcinilor, după cum puteți vedea, simplu, scurt și inofensiv. Dar cu această formulă de rădăcină, poți face o mulțime de lucruri utile! Să aruncăm o privire la exemple toate aceste lucruri utile.

Lucru util în primul rând. Această formulă ne permite inmulti radacinile.

Cum să înmulțim rădăcinile?

Da, foarte simplu. Direct la formula. De exemplu:

S-ar părea că s-au înmulțit, deci ce? Există multă bucurie? Sunt de acord, puțin. Dar cum iti place asta exemplu?

Rădăcinile nu sunt extrase tocmai din factori. Iar rezultatul este grozav! Deja mai bine, nu? Pentru orice eventualitate, vă voi informa că pot exista oricât de mulți multiplicatori doriți. Formula de multiplicare a rădăcinilor încă funcționează. De exemplu:

Deci, cu înmulțirea, totul este clar de ce este nevoie de acest lucru proprietatea rădăcinilor- este, de asemenea, de înțeles.

Lucru util al doilea. Introducerea unui număr sub semnul rădăcinii.

Cum se introduce un număr sub rădăcină?

Să presupunem că avem această expresie:

Este posibil să ascundeți deuce în interiorul rădăcinii? Uşor! Dacă faceți o rădăcină din două, formula de înmulțire a rădăcinilor va funcționa. Și cum să faci o rădăcină dintr-un doi? Da, nici asta nu este o întrebare! Dublul este rădăcină pătrată de patru!

Rădăcina, apropo, poate fi făcută din orice număr nenegativ! Aceasta va fi rădăcina pătrată a pătratului acestui număr. 3 este rădăcina lui 9. 8 este rădăcina lui 64. 11 este rădăcina lui 121. Ei bine, și așa mai departe.

Desigur, nu este nevoie să pictezi atât de detaliat. Cu excepția, pentru început. Este suficient să ne dăm seama că orice număr nenegativ înmulțit cu rădăcină poate fi adus sub rădăcină. Dar nu uita! - sub rădăcină acest număr va deveni pătrat se. Această acțiune - introducerea unui număr sub rădăcină - poate fi numită și înmulțirea unui număr cu rădăcină. În termeni generali, se poate scrie:

Procesul este simplu, după cum puteți vedea. De ce este nevoie de ea?

Ca orice transformare, această procedură ne extinde posibilitățile. Oportunități de a transforma o expresie crudă și incomodă într-una moale și pufoasă). Iată unul simplu pentru tine exemplu:

După cum puteți vedea proprietate rădăcină, care face posibilă introducerea unui factor sub semnul rădăcinii, este destul de potrivită pentru simplificare.

În plus, adăugarea unui multiplicator sub rădăcină face ușoară și simplă compararea valorilor diferitelor rădăcini. Fara calcul si calculator! Al treilea lucru util.

Cum se compară rădăcinile?

Această abilitate este foarte importantă în misiuni solide, la deblocarea modulelor și alte lucruri interesante.

Comparați aceste expresii. Care este mai mult? Fără calculator! Fiecare cu un calculator. uh-uh. Pe scurt, toată lumea o poate face!)

Nu spui asta imediat. Și dacă introduci numere sub semnul rădăcinii?

Amintiți-vă (deodată, nu știați?): dacă numărul de sub semnul rădăcinii este mai mare, atunci rădăcina în sine este mai mare! De aici răspunsul imediat corect, fără calcule și calcule complicate:

E grozav, nu? Dar asta nu este tot! Amintiți-vă că toate formulele funcționează atât de la stânga la dreapta, cât și de la dreapta la stânga. Am folosit până acum formula pentru înmulțirea rădăcinilor de la stânga la dreapta. Să rulăm această proprietate rădăcină înapoi, de la dreapta la stânga. Ca aceasta:

Și care este diferența? Îți dă ceva!? Cu siguranță! Acum vei vedea singur.

Să presupunem că trebuie să extragem (fără calculator!) rădăcina pătrată a numărului 6561. Unii oameni în această etapă vor cădea într-o luptă inegală cu sarcina. Dar suntem încăpățânați, nu renunțăm! Lucru util al patrulea.

Cum să extragi rădăcini din un număr mare?

Reamintim formula pentru extragerea rădăcinilor dintr-un produs. Cel pe care l-am postat mai sus. Dar unde este munca noastră? Avem un număr mare 6561 și atât. Da, nu există artă. Dar dacă avem nevoie, noi Hai sa facem! Să factorizez acest număr. Avem dreptul.

Mai întâi, să ne dăm seama cu ce acest număr este divizibil exact? Ce, nu știi!? Ai uitat semnele de divizibilitate!? Degeaba. Mergeți la Secțiunea Specială 555, subiectul „Fracțiuni”, acolo sunt. Acest număr este divizibil cu 3 și 9. Deoarece suma cifrelor (6+5+6+1=18) este divizibilă cu aceste numere. Acesta este unul dintre semnele divizibilității. Nu trebuie să împărțim la trei (acum veți înțelege de ce), dar vom împărți la 9. Cel puțin într-un colț. Primim 729. Deci am găsit doi factori! Primul este un nouă (noi l-am ales noi), iar al doilea este 729 (așa a ieșit). Deja poți scrie:

Înțelegi ideea? Să facem același lucru cu numărul 729. De asemenea, este divizibil cu 3 și 9. Din nou, nu împărțim la 3, împărțim la 9. Obținem 81. Și știm acest număr! Scriem:

Totul a ieșit ușor și elegant! Rădăcina a trebuit îndepărtată bucată cu bucată, bine, bine. Acest lucru se poate face cu orice număr mare. Înmulțiți-le și plecați!

Apropo, de ce nu ai trebuit să împărți la 3, ai ghicit? Da, pentru că rădăcina lui trei nu este tocmai extrasă! Este logic să se descompună în astfel de factori încât cel puțin o rădăcină să poată fi extrasă bine. Este 4, 9, 16 bine și așa mai departe. Împărțiți pe rând numărul vostru uriaș la aceste numere, vedeți și aveți noroc!

Dar nu neapărat. Poate nu norocos. Să presupunem că numărul 432, atunci când este factorizat și utilizând formula rădăcină pentru produs, va da următorul rezultat:

Ei bine, bine. Am simplificat expresia oricum. În matematică, se obișnuiește să se lase cel mai mic număr posibil sub rădăcină. În procesul de rezolvare, totul depinde de exemplu (poate că totul este redus fără simplificare), dar în răspuns este necesar să se dea un rezultat care nu poate fi simplificat în continuare.

Apropo, știți ce am făcut acum cu rădăcina lui 432?

Noi factori scoși de sub semnul rădăcinii ! Așa se numește această operațiune. Și atunci sarcina va cădea - " scoateți factorul de sub semnul rădăcinii„Dar bărbații nici măcar nu știu.) Iată o altă utilizare pentru tine proprietățile rădăcinii. Lucru util al cincilea.

Cum să scoți multiplicatorul de sub rădăcină?

Uşor. Factorizați expresia rădăcinii și extrageți rădăcinile care sunt extrase. Ne uitam:

Nimic supranatural. Este important să alegeți multiplicatorii potriviți. Aici am descompus 72 ca 36 2. Și totul a ieșit bine. Sau ar fi putut-o descompune diferit: 72 = 6 12. Si ce!? Nici de la 6, nici de la 12 nu se extrage radacina. Ce să fac?!

E bine. Sau căutați alte opțiuni de descompunere sau continuați să puneți totul până la capăt! Ca aceasta:

După cum puteți vedea, totul a funcționat. Acesta, apropo, nu este cel mai rapid, ci cel mai fiabil mod. Descompuneți numărul în cei mai mici factori, apoi colectați aceiași în grămezi. Metoda este, de asemenea, aplicată cu succes la înmulțirea rădăcinilor incomode. De exemplu, trebuie să calculați:

Înmulțiți totul - obțineți un număr nebun! Și apoi cum să extragi rădăcina din ea?! Înmulțiți din nou? Nu, nu avem nevoie de muncă suplimentară. Ne descompunem imediat în factori și îi colectăm în grămezi:

Asta e tot. Desigur, nu este necesar să vă așezați până la oprire. Totul este determinat de abilitățile tale personale. A adus exemplul într-o stare în care totul este clar pentru tine asa ca poti sa numeri deja. Principalul lucru este să nu faci greșeli. Nu un om pentru matematică, ci matematică pentru un bărbat!)

Să aplicăm cunoștințele în practică? Să începem cu unul simplu:

Regula pentru adăugarea rădăcinilor pătrate

Proprietățile rădăcinilor pătrate

Până acum, am efectuat cinci operații aritmetice pe numere: adunare, scădere, multiplicare, împărțirea și exponentiația și diverse proprietăți ale acestor operații au fost utilizate în mod activ în calcule, de exemplu, a + b = b + a și n -b n = (ab) n etc.

Acest capitol introduce o nouă operație - luarea rădăcinii pătrate a unui număr nenegativ. Pentru a-l folosi cu succes, trebuie să vă familiarizați cu proprietățile acestei operațiuni, pe care le vom face în această secțiune.

Dovada. Să introducem următoarea notație:
Trebuie să demonstrăm că pentru numerele nenegative x, y, z egalitatea x = yz este adevărată.

Deci x 2 = ab, y 2 = a, z 2 = b. Atunci x 2 \u003d y 2 z 2, adică x 2 \u003d (yz) 2.

Dacă pătrate două numere nenegative sunt egale, atunci numerele în sine sunt egale, ceea ce înseamnă că din egalitatea x 2 \u003d (yz) 2 rezultă că x \u003d yz, iar acest lucru trebuia demonstrat.

Oferim o scurtă înregistrare a demonstrației teoremei:

Observație 1. Teorema rămâne valabilă pentru cazul în care expresia radicală este produsul a mai mult de doi factori nenegativi.

Observația 2. Teorema 1 poate fi scris folosind „dacă. , apoi” (cum se obișnuiește pentru teoremele din matematică). Dăm formula corespunzătoare: dacă a și b sunt numere nenegative, atunci egalitatea .

Așa formulăm următoarea teoremă.

(O formulare scurtă care este mai convenabilă de utilizat în practică: rădăcina unei fracții este egală cu fracția rădăcinilor sau rădăcina coeficientului este egală cu coeficientul rădăcinilor.)

De data aceasta vom oferi doar o scurtă înregistrare a demonstrației și puteți încerca să faceți comentarii adecvate, similare cu cele care au alcătuit esența demonstrației teoremei 1.

Exemplul 1. Calculați .
Soluţie. Folosind prima proprietate rădăcini pătrate(Teorema 1), obținem

Observația 3. Desigur, acest exemplu poate fi rezolvat diferit, mai ales dacă aveți un calculator la îndemână: înmulțiți numerele 36, 64, 9, apoi luați rădăcina pătrată a produsului rezultat. Cu toate acestea, veți fi de acord că soluția propusă mai sus arată mai culturală.

Observația 4. În prima metodă, am efectuat calcule frontale. A doua modalitate este mai elegantă:
am aplicat formulă a 2 - b 2 \u003d (a - b) (a + b) și a folosit proprietatea rădăcinilor pătrate.

Observația 5. Unii „capete fierbinți” oferă uneori următoarea „soluție” pentru Exemplul 3:

Acest lucru, desigur, nu este adevărat: vedeți - rezultatul nu este același ca în exemplul nostru 3. Faptul este că nu există nicio proprietate ca nu si proprietati Există doar proprietăți referitoare la înmulțirea și împărțirea rădăcinilor pătrate. Fii atent și atent, nu accepta iluzii.

Exemplul 4. Calculați: a)
Soluţie. Orice formulă în algebră este folosită nu numai „de la dreapta la stânga”, ci și „de la stânga la dreapta”. Deci, prima proprietate a rădăcinilor pătrate înseamnă că, dacă este necesar, poate fi reprezentată ca și invers, care poate fi înlocuită cu expresia Același lucru este valabil și pentru a doua proprietate a rădăcinilor pătrate. Având în vedere acest lucru, să rezolvăm exemplul propus.

În încheierea paragrafului, remarcăm încă o proprietate destul de simplă și în același timp importantă:
dacă a > 0 și n - numar natural, Acea

Exemplul 5 calculati , fără a folosi un tabel de pătrate de numere și un calculator.

Soluţie. Să descompunăm numărul rădăcină în factori primi:

Observația 6. Acest exemplu ar putea fi rezolvat în același mod ca exemplul similar din § 15. Este ușor de ghicit că răspunsul va fi „80 cu coadă”, deoarece 80 2 2 . Să găsim „coada”, adică ultima cifră a numărului dorit. Până acum știm că dacă se extrage rădăcina, atunci răspunsul poate fi 81, 82, 83, 84, 85, 86, 87, 88 sau 89. Trebuie verificate doar două numere: 84 și 86, deoarece doar ele, la pătrat, va da ca rezultat patru cifre un număr care se termină cu 6, adică aceeași cifră care se termină cu numărul 7056. Avem 84 2 \u003d 7056 - de asta avem nevoie. Mijloace,

Mordkovich A. G., Algebră. Clasa 8: Proc. pentru învăţământul general instituţii.- ed. a III-a, finalizat. - M.: Mnemosyne, 2001. - 223 p.: ill.

Cărți, manuale de matematică descărcate, rezumate pentru a ajuta profesorul și elevii să învețe online

Dacă aveți corecții sau sugestii pentru această lecție, scrieți-ne.

Dacă doriți să vedeți alte corecții și sugestii pentru lecții, vedeți aici - Forumul Educației.

Cum să adăugați rădăcini pătrate

Rădăcina pătrată a unui număr X numit un număr A, care în procesul de a se înmulți singur ( A*A) poate da un număr X.
Acestea. A * A = A 2 = X, Și √X = A.

Peste rădăcini pătrate ( √x), ca și în cazul altor numere, puteți efectua operații aritmetice precum scăderea și adunarea. Pentru a scădea și a adăuga rădăcini, acestea trebuie conectate folosind semne corespunzătoare acestor acțiuni (de exemplu √x - √y ).
Și apoi aduceți rădăcinile la forma lor cea mai simplă - dacă există altele similare între ele, trebuie să faceți o turnare. Constă în faptul că coeficienții termenilor similari sunt luați cu semnele termenilor corespunzători, apoi sunt încadrați între paranteze și rădăcina comună este afișată în afara parantezelor multiplicatoare. Coeficientul pe care l-am obținut este simplificat conform regulilor uzuale.

Pasul 1. Extragerea rădăcinilor pătrate

În primul rând, pentru a adăuga rădăcini pătrate, trebuie mai întâi să extragi aceste rădăcini. Acest lucru se poate face dacă numerele de sub semnul rădăcinii sunt pătrate perfecte. De exemplu, luați expresia dată √4 + √9 . Primul număr 4 este pătratul numărului 2 . Al doilea număr 9 este pătratul numărului 3 . Astfel, se poate obține următoarea egalitate: √4 + √9 = 2 + 3 = 5 .
Totul, exemplul este rezolvat. Dar nu întotdeauna se întâmplă așa.

Pasul 2. Scoaterea multiplicatorului unui număr de sub rădăcină

Dacă nu există pătrate întregi sub semnul rădăcinii, puteți încerca să scoateți multiplicatorul numărului de sub semnul rădăcinii. De exemplu, luați expresia √24 + √54 .

Să factorizăm numerele:
24 = 2 * 2 * 2 * 3 ,
54 = 2 * 3 * 3 * 3 .

Printre 24 avem un multiplicator 4 , poate fi scos de sub semnul rădăcinii pătrate. Printre 54 avem un multiplicator 9 .

Obținem egalitatea:
√24 + √54 = √(4 * 6) + √(9 * 6) = 2 * √6 + 3 * √6 = 5 * √6 .

Luând în considerare acest exemplu, obținem eliminarea factorului de sub semnul rădăcinii, simplificând astfel expresia dată.

Pasul 3. Reducerea numitorului

Luați în considerare următoarea situație: suma a două rădăcini pătrate este numitorul unei fracții, de exemplu, A / (√a + √b).
Acum ne confruntăm cu sarcina de a „scăpa de iraționalitatea din numitor”.
Să folosim următoarea metodă: înmulțiți numărătorul și numitorul fracției cu expresia √a - √b.

Acum obținem formula de înmulțire prescurtată la numitor:
(√a + √b) * (√a - √b) = a - b.

În mod similar, dacă numitorul conține diferența rădăcinilor: √a - √b, numărătorul și numitorul fracției se înmulțesc cu expresia √a + √b.

Să luăm ca exemplu o fracție:
4 / (√3 + √5) = 4 * (√3 — √5) / ((√3 + √5) * (√3 — √5)) = 4 * (√3 — √5) / (-2) = 2 * (√5 — √3) .

Un exemplu de reducere complexă a numitorului

Acum vom lua în considerare un exemplu destul de complicat de a scăpa de iraționalitate în numitor.

Să luăm ca exemplu o fracție: 12 / (√2 + √3 + √5) .
Trebuie să luați numărătorul și numitorul și să înmulțiți cu expresia √2 + √3 — √5 .

12 / (√2 + √3 + √5) = 12 * (√2 + √3 — √5) / (2 * √6) = 2 * √3 + 3 * √2 — √30.

Pasul 4. Calculați valoarea aproximativă pe calculator

Dacă aveți nevoie doar de o valoare aproximativă, aceasta se poate face pe un calculator calculând valoarea rădăcinilor pătrate. Separat, pentru fiecare număr, valoarea este calculată și înregistrată cu precizia necesară, care este determinată de numărul de zecimale. În plus, toate operațiunile necesare sunt efectuate, ca și în cazul numerelor obișnuite.

Exemplu de calcul estimat

Este necesar să se calculeze valoarea aproximativă a acestei expresii √7 + √5 .

Ca rezultat, obținem:

√7 + √5 ≈ 2,65 + 2,24 = 4,89 .

Vă rugăm să rețineți: în niciun caz nu trebuie adăugate rădăcini pătrate ca numere prime, acest lucru este complet inacceptabil. Adică, dacă adăugați rădăcina pătrată a lui cinci și trei, nu putem obține rădăcina pătrată a lui opt.

Sfat util: dacă decideți să factorizați un număr, pentru a deriva un pătrat de sub semnul rădăcinii, trebuie să faceți o verificare inversă, adică să înmulțiți toți factorii care au rezultat din calcule și rezultatul final al acestuia. calculul matematic ar trebui să fie numărul care ni s-a dat inițial.

Acțiune cu rădăcini: adunare și scădere

Extragerea rădăcinii pătrate a unui număr nu este singura operație care poate fi efectuată cu acest fenomen matematic. La fel ca numerele obișnuite, rădăcinile pătrate pot fi adunate și scăzute.

Reguli pentru adăugarea și scăderea rădăcinilor pătrate

Acțiuni precum adăugarea și scăderea unei rădăcini pătrate sunt posibile numai dacă expresia rădăcinii este aceeași.

Puteți adăuga sau scădea expresii 2 3 și 6 3, dar nu 5 6 Și 9 4 . Dacă este posibil să simplificați expresia și să o aduceți la rădăcini cu același număr de rădăcină, atunci simplificați și apoi adăugați sau scădeți.

Acțiunile rădăcină: elementele de bază

6 50 — 2 8 + 5 12

1. Simplificați expresia rădăcină. Pentru a face acest lucru, este necesar să descompuneți expresia rădăcinii în 2 factori, dintre care unul este un număr pătrat (numărul din care este extrasă întreaga rădăcină pătrată, de exemplu, 25 sau 9).
2. Apoi trebuie să luați rădăcina numărului pătratși scrieți valoarea rezultată înainte de semnul rădăcină. Vă rugăm să rețineți că al doilea factor este introdus sub semnul rădăcină.
3. După procesul de simplificare, este necesar să se sublinieze rădăcinile cu aceleași expresii radicale - doar ele pot fi adăugate și scăzute.
4. Pentru rădăcinile cu aceleași expresii radicale, este necesar să se adauge sau să scadă factorii care preced semnul rădăcinii. Expresia rădăcină rămâne neschimbată. Nu adăugați sau scădeți numere de rădăcină!

Dacă aveți un exemplu cu o mulțime de expresii radicale identice, atunci subliniați astfel de expresii cu linii simple, duble și triple pentru a facilita procesul de calcul.

Să încercăm acest exemplu:

6 50 = 6 (25 × 2) = (6 × 5) 2 = 30 2 . Mai întâi trebuie să descompuneți 50 în 2 factori 25 și 2, apoi luați rădăcina lui 25, care este 5, și scoateți 5 de sub rădăcină. După aceea, trebuie să înmulțiți 5 cu 6 (multiplicatorul de la rădăcină) și să obțineți 30 2 .

2 8 = 2 (4 × 2) = (2 × 2) 2 = 4 2 . Mai întâi, trebuie să descompuneți 8 în 2 factori: 4 și 2. Apoi, din 4, extrageți rădăcina, care este egală cu 2, și scoateți 2 de sub rădăcină. După aceea, trebuie să înmulțiți 2 cu 2 (factorul de la rădăcină) și să obțineți 4 2 .

5 12 = 5 (4 × 3) = (5 × 2) 3 = 10 3 . Mai întâi, trebuie să descompuneți 12 în 2 factori: 4 și 3. Apoi extrageți rădăcina din 4, care este 2, și scoateți-o de sub rădăcină. După aceea, trebuie să înmulțiți 2 cu 5 (factorul de la rădăcină) și să obțineți 10 3 .

Rezultat simplificare: 30 2 — 4 2 + 10 3

30 2 — 4 2 + 10 3 = (30 — 4) 2 + 10 3 = 26 2 + 10 3 .

Ca rezultat, am văzut câte expresii radicale identice sunt conținute în acest exemplu. Acum să exersăm cu alte exemple.

• Simplificați (45) . Factorizăm 45: (45) = (9 × 5) ;
• Scoatem 3 de sub rădăcină (9 \u003d 3): 45 \u003d 3 5;
• Adunăm factorii de la rădăcini: 3 5 + 4 5 = 7 5 .
• Simplificarea 6 40 . Factorizăm 40: 6 40 \u003d 6 (4 × 10) ;
• Scoatem 2 de sub rădăcină (4 \u003d 2): 6 40 \u003d 6 (4 × 10) \u003d (6 × 2) 10;
• Înmulțim factorii care se află în fața rădăcinii: 12 10;
• Scriem expresia într-o formă simplificată: 12 10 - 3 10 + 5;
• Deoarece primii doi termeni au aceleași numere de rădăcină, le putem scădea: (12 - 3) 10 = 9 10 + 5.

După cum putem vedea, nu este posibilă simplificarea numerelor radicale, prin urmare, în exemplu, căutăm membri cu aceleași numere radicale, efectuăm operații matematice (adunare, scădere etc.) și scriem rezultatul:

(9 — 4) 5 — 2 3 = 5 5 — 2 3 .

Sfat:

• Înainte de a adăuga sau scădea, este imperativ să simplificați (dacă este posibil) expresiile radicale.
• Adăugarea și scăderea rădăcinilor cu expresii de rădăcină diferite este strict interzisă.
• Nu adăugați sau scădeți un număr întreg sau rădăcină pătrată: 3 + (2 x) 1 / 2 .
• Când efectuați acțiuni cu fracții, trebuie să găsiți un număr care este divizibil cu fiecare numitor, apoi aduceți fracțiile la un numitor comun, apoi adăugați numărătorii și lăsați numitorii neschimbați.

Proprietățile rădăcinii pătrate aritmetice. Puterea rădăcinii pătrate aritmetice

Conversia rădăcinilor pătrate aritmetice. Conversia rădăcinilor pătrate aritmetice

A extrage rădăcina pătrată a unui polinom, este necesar să se calculeze polinomul și să se extragă rădăcina din numărul rezultat.

Atenţie! Este imposibil să extragi rădăcina din fiecare termen (redus și scăzut) separat.

Shchob să câștige rădăcină pătrată a polinomului, cerința este să se calculeze termenul bogat și din numărul scăzut să se ia rădăcina.

Respect! Este imposibil să extragi rădăcina din suplimentul de piele (schimbat și vizibil) OKremo.

Pentru a extrage rădăcina pătrată a produsului (coeficient), puteți calcula rădăcina pătrată a fiecărui factor (dividend și divizor) și luați valorile rezultate după produs (cot).

Pentru a câștiga rădăcina pătrată a dobutka (părți), puteți calcula rădăcina pătrată a multiplicatorului de piele (divizat și dilnik) și puteți elimina valoarea luând un suplimentar (frecvent).

Pentru a lua rădăcina pătrată a unei fracții, trebuie să extrageți separat rădăcina pătrată a numărătorului și numitorului și lăsați valorile rezultate ca o fracție sau să calculați ca un coeficient (dacă este posibil prin condiție).

Pentru a câștiga rădăcina pătrată a fracției, trebuie să luați rădăcina pătrată a cărții de numere și steagul okremo și să privați valoarea fracției cu o fracție sau să o numărați ca parte (cum este posibil pentru minte).

Un factor poate fi scos de sub semnul rădăcinii și un factor poate fi introdus sub semnul rădăcinii. Când un factor este scos, rădăcina este extrasă din el, iar când este introdusă, este ridicată la puterea corespunzătoare.

Al treilea semn rădăcină poate fi înmulțit, iar semnul rădăcină poate fi înmulțit. Din vina multiplicatorului, rădăcinile sunt răsucite, iar odată cu introducerea, rădăcinile sunt construite la picioarele mai înalte.

Exemple. aplica

Pentru a converti suma (diferența) rădăcinilor pătrate, trebuie să aduceți expresiile rădăcinii la o bază a gradului, dacă este posibil, extrageți rădăcinile din grade și scrieți-le înaintea semnelor rădăcinilor, iar rădăcinile pătrate rămase cu se pot adăuga aceleași expresii de rădăcină, pentru care se adaugă coeficienții înaintea rădăcinii semnului și se adaugă aceeași rădăcină pătrată.

Pentru a reface suma (costul) rădăcinilor pătrate, este necesar să aduceți rădăcinile sub-rădăcinii la una dintre bazele pasului, după cum este posibil, să faceți pașii rădăcinii și să le scrieți înaintea semnelor rădăcini, și puteți rezolva rădăcinile pătrate cu aceeași rădăcină rădăcină se adună, pentru care coeficienții se adaugă în fața semnului rădăcinii și se adaugă aceeași rădăcină pătrată.

Aducem toate expresiile radicale la baza 2.

Din grad par se extrage complet rădăcina, dintr-un grad impar rădăcina bazei de gradul 1 se lasă sub semnul rădăcinii.

Oferim numere întregi similare și adăugăm coeficienții cu aceleași rădăcini. Scriem binomul ca produs al unui număr și binomul sumei.

Aduceți toate subrădăcinile virazi la baza 2.

Din stadiul pereche, rădăcinile sunt desenate pe rând, din stadiul nepereche, rădăcinile bazei din stadiul 1 sunt umplute sub semnul rădăcinii.

Se sugerează că la aceleași rădăcini se adaugă numere și coeficienți similari. Scriem binomul ca supliment al numărului i al binomului sumi.

Aducem expresiile radicale la cea mai mică bază sau produsul puterilor cu cele mai mici baze. Extragem rădăcina din grade egale de expresii radicale, lăsăm resturile sub forma unei baze de grad cu un indicator de 1 sau produsul unor astfel de baze sub semnul rădăcinii. Oferim termeni similari (adăugăm coeficienții acelorași rădăcini).

Conducem rădăcina virazilor la cea mai mică bază sau adăugarea de trepte cu cele mai mici baze. Din treptele vaporoase de sub rădăcinile virazului se iau rădăcinile, surplusul de la baza treptei cu indicatorul 1 sau adăugarea unor astfel de baze se umple sub semnul rădăcinii. Sugerăm termeni similari (adunăm coeficienții acelorași rădăcini).

Să înlocuim împărțirea fracțiilor cu înmulțirea (cu înlocuirea celei de-a doua fracții cu reciprocă). Înmulțiți separat numărătorii și numitorii. Sub fiecare semn al rădăcinii, evidențiem gradele. Să anulăm aceiași factori la numărător și numitor. Extragem rădăcini din puterile egale.

Înlocuim împărțirea fracțiilor cu o înmulțire (cu înlocuirea unei alte fracții cu un randament). Înmulțiți numere okremo și bannere de fracții. Pașii sunt vizibili sub semnul pielii rădăcinii. Vom accelera aceiași multiplicatori în cartea de numere și banner. Da vina pe rădăcina treptelor gemene.

Pentru a compara două rădăcini pătrate, expresiile lor radicale trebuie reduse la un grad cu aceeași bază, atunci cu cât sunt afișate mai multe grade de expresie radicală, cu atât valoarea rădăcinii pătrate este mai mare.

În acest exemplu, expresiile radicale nu pot fi reduse la o singură bază, deoarece baza este 3 în prima și 3 și 7 în a doua.

A doua modalitate de comparare este să introduceți coeficientul rădăcinii în expresia radicală și să comparați valorile numerice ale expresiilor radicale. Pentru o rădăcină pătrată, cu cât expresia rădăcinii este mai mare, cu atât valoarea rădăcinii este mai mare.

Pentru a potrivi două rădăcini pătrate, subrădăcinile lor trebuie aduse la un nivel cu aceeași bază, în timp ce cu cât indicatorul gradului subrădăcinii virusului este mai mare, cu atât valoarea rădăcinii pătrate este mai mare.

În acest caz, nu este posibil să se aducă la o bază rădăcinile rădăcinii virazi, deoarece în prima baza este 3, iar în cealaltă - 3 și 7.

O altă modalitate de a egaliza este să adăugați coeficientul rădăcină la viraza rădăcină și să egalizați valorile numerice ale virasei rădăcină. Rădăcina pătrată are mai mult sub-rădăcină viraz, cu atât mai multă valoare a rădăcinii.

Folosind legea distributivă a înmulțirii și regula înmulțirii rădăcinilor cu aceiași exponenți (în cazul nostru, rădăcini pătrate), am obținut suma a două rădăcini pătrate cu produsul sub semnul rădăcinii. Descompunem 91 în factori primi și scoatem rădăcina din paranteze cu factori radicali comuni (13 * 5).

Am obținut produsul dintre o rădăcină și un binom, în care unul dintre monomii este un număr întreg (1).

Vikoristovuyuchi rozpodilny legea înmulțirii și regula înmulțirii rădăcinilor cu aceiași indicatori (în cazul nostru - rădăcini pătrate), au luat suma a două rădăcini pătrate cu un semn suplimentar al rădăcinii. Putem așeza 91 de multiplicatori în termeni simpli și putem lua rădăcina pentru arcade din multiplicatorii de rădăcină (13 * 5).

Am luat adunarea unei rădăcini și a unui binar, care are unul dintre mononoamele în întregul număr (1).

Exemplul 9:

În expresiile radicale, selectăm prin factori numerele din care putem extrage întreaga rădăcină pătrată. Extragem rădăcinile pătrate din puteri și punem numerele după coeficienții rădăcinilor pătrate.

Termenii acestui polinom au un factor comun √3, care poate fi scos din paranteze. Să prezentăm termeni similari.

În virasele sub-rădăcină, este văzut ca multiplicatori ai numărului, din care se poate lua rădăcina pătrată. Dăm vina pe rădăcinile pătrate ale treptelor și punem numerele după coeficienții rădăcinilor pătrate.

Termenii acestui polinom au un multiplicator comun √3, care poate fi acuzat pentru brațe. Vă sugerăm completări similare.

Produsul sumei și diferenței a două baze identice (3 și √5) poate fi scris folosind formula de înmulțire prescurtată ca diferență a pătratelor bazelor.

Rădăcina pătrată pătrată este întotdeauna egală cu expresia radicală, așa că vom scăpa de radicalul (semnul rădăcinii) din expresie.

Dobutok suma și diferența a două baze identice (3 і √5) din formula de înmulțire rapidă pot fi scrise ca diferență de baze pătrate.

Rădăcina pătrată a zavzhd pătrată este egală cu sub-rădăcina virasei, așa că vom numi radicalul (semnul rădăcinii) virasei.

Înapoi la școală. Adăugarea de rădăcini

În vremea computerelor electronice moderne, calcularea rădăcinii unui număr nu este o sarcină dificilă. De exemplu, √2704=52, orice calculator va calcula acest lucru pentru tine. Din fericire, calculatorul nu este doar în Windows, ci și într-un telefon obișnuit, chiar și cel mai simplu. Adevărat, dacă dintr-o dată (cu un grad mic de probabilitate, al cărui calcul, apropo, include adăugarea de rădăcini) te trezești fără fonduri disponibile, atunci, din păcate, va trebui să te bazezi doar pe creierul tău.

Antrenamentul minții nu eșuează niciodată. Mai ales pentru cei care nu lucrează cu numere atât de des și cu atât mai mult cu rădăcini. Adăugarea și scăderea rădăcinilor este un antrenament bun pentru o minte plictisită. Și vă voi arăta adăugarea rădăcinilor pas cu pas. Exemple de expresii pot fi următoarele.

Ecuația de simplificat este:

Aceasta este o expresie irațională. Pentru a o simplifica, trebuie să aduceți toate expresiile radicale într-o formă comună. O facem în etape:

Primul număr nu mai poate fi simplificat. Să trecem la al doilea termen.

3√48 factorizăm 48: 48=2×24 sau 48=3×16. Rădăcina pătrată a lui 24 nu este un număr întreg, adică are un rest fracționar. Deoarece avem nevoie de o valoare exactă, rădăcinile aproximative nu sunt potrivite pentru noi. Rădăcina pătrată a lui 16 este 4, scoate-o de sub semnul rădăcinii. Se obține: 3×4×√3=12×√3

Următoarea noastră expresie este negativă, adică. scris cu semnul minus -4×√(27.) Factorizarea 27. Obținem 27=3×9. Nu folosim factori fracționari, deoarece este mai dificil să calculăm rădăcina pătrată din fracții. Scoatem 9 de sub semn, adică. calculați rădăcina pătrată. Obținem următoarea expresie: -4×3×√3 = -12×√3

Următorul termen √128 calculează partea care poate fi scoasă de sub rădăcină. 128=64×2 unde √64=8. Dacă vă este mai ușor, puteți reprezenta această expresie astfel: √128=√(8^2×2)

Rescriem expresia cu termeni simplificați:

Acum adăugăm numerele cu aceeași expresie radicală. Nu puteți adăuga sau scădea expresii cu expresii radicale diferite. Adăugarea de rădăcini necesită respectarea acestei reguli.

Obținem următorul răspuns:

√2=1×√2 - Sper că este obișnuit în algebră să omiteți astfel de elemente să nu fie o noutate pentru dvs.

Expresiile pot fi reprezentate nu numai prin rădăcini pătrate, ci și prin rădăcini cubice sau a n-a.

Adunarea și scăderea rădăcinilor cu exponenți diferiți, dar cu o expresie echivalentă a rădăcinilor, se produce după cum urmează:

Dacă avem o expresie ca √a+∛b+∜b, atunci putem simplifica această expresie astfel:

12√b4 +12×√b3=12×√b4 + b3

Am redus doi termeni similari la exponentul comun al rădăcinii. Aici a fost folosită proprietatea rădăcinilor, care spune: dacă numărul gradului expresiei radicalului și numărul exponentului rădăcinii sunt înmulțite cu același număr, atunci calculul său va rămâne neschimbat.

Notă: exponenții sunt adăugați numai atunci când sunt înmulțiți.

Luați în considerare un exemplu în care fracțiile sunt prezente într-o expresie.

Să rezolvăm pas cu pas:

5√8=5*2√2 - scoatem partea extrasă de sub rădăcină.

Dacă corpul rădăcinii este reprezentat de o fracție, atunci de multe ori această fracție nu se va schimba dacă se ia rădăcina pătrată a dividendului și a divizorului. Ca rezultat, am obținut egalitatea descrisă mai sus.

Iată răspunsul.

Principalul lucru de reținut este că o rădăcină cu exponent par nu este extrasă din numerele negative. Dacă o expresie radicală de grad egal este negativă, atunci expresia este de nerezolvat.

Adăugarea rădăcinilor este posibilă numai dacă expresiile radicale coincid, deoarece sunt termeni similari. Același lucru este valabil și pentru diferență.

Adăugarea rădăcinilor cu exponenți numerici diferiți se realizează prin reducerea ambilor termeni la un grad comun de rădăcină. Această lege funcționează în același mod ca și reducerea la un numitor comun la adunarea sau scăderea fracțiilor.

Dacă expresia radicală conține un număr ridicat la o putere, atunci această expresie poate fi simplificată cu condiția ca între rădăcină și exponent să existe un numitor comun.

Rădăcina pătrată a unui produs și a unei fracții

Rădăcina pătrată a lui a este un număr al cărui pătrat este a. De exemplu, numerele -5 și 5 sunt rădăcinile pătrate ale numărului 25. Adică, rădăcinile ecuației x^2=25 sunt rădăcinile pătrate ale numărului 25. Acum trebuie să învățați cum să lucrați cu operația cu rădăcina pătrată: studiați proprietățile sale de bază.

Rădăcina pătrată a produsului

√(a*b)=√a*√b

Rădăcina pătrată a produsului a două numere nenegative este egală cu produsul rădăcinilor pătrate ale acestor numere. De exemplu, √(9*25) = √9*√25 =3*5 =15;

Este important de înțeles că această proprietate se aplică și în cazul în care expresia radicală este produsul lui trei, patru etc. multiplicatori nenegativi.

Uneori există o altă formulare a acestei proprietăți. Dacă a și b sunt numere nenegative, atunci este valabilă următoarea egalitate: √(a*b) =√a*√b. Nu există absolut nicio diferență între ele, puteți folosi fie una, fie cealaltă formulare (care este mai convenabil de reținut).

Rădăcina pătrată a unei fracții

Dacă a>=0 și b>0, atunci următoarea egalitate este adevărată:

√(a/b)=√a/√b.

De exemplu, √(9/25) = √9/√25 =3/5;

Această proprietate are și o formulare diferită, în opinia mea, mai convenabil de reținut.
Rădăcina pătrată a câtului este egală cu câtul rădăcinilor.

Este de remarcat faptul că aceste formule funcționează atât de la stânga la dreapta, cât și de la dreapta la stânga. Adică, dacă este necesar, putem reprezenta produsul rădăcinilor ca rădăcină a produsului. Același lucru este valabil și pentru a doua proprietate.

După cum puteți vedea, aceste proprietăți sunt foarte convenabile și aș dori să am aceleași proprietăți pentru adunare și scădere:

√(a+b)=√a+√b;

√(a-b)=√a-√b;

Dar, din păcate, astfel de proprietăți sunt pătrate nu au rădăcini, și așa nu se poate face în calcule..

• 13. Conducerea prin intersecții de trafic 2018 cu comentarii online 13.1. La virajul la dreapta sau la stânga, șoferul trebuie să cedeze pietonii și bicicliștii care traversează carosabilul pe care vira. Această instrucțiune se aplică tuturor […]
• Întâlnirea părinților „Drepturile, îndatoririle și responsabilitățile părinților” Prezentare pentru lecție Descărcați prezentarea (536.6 kB) Atenție! Previzualizarea slide-ului are doar scop informativ și este posibil să nu reprezinte toate […]
• Capitala maternității regionale din regiunea Orel Capitala maternității regionale (MC) din Orel și regiunea Oryol a fost înființată în 2011. Acum este o măsură suplimentară de sprijin social pentru familiile numeroase, sub forma unei […]
• Valoarea unei alocații unice pentru înregistrarea timpurie în 2018 Pagina pe care ați solicitat-o ​​nu a fost găsită. Este posibil să fi introdus o adresă greșită sau pagina a fost eliminată. Utilizare […]
• Avocat în Afaceri Economice Crimele în sfera economică este un concept destul de voluminos. Astfel de acte includ fraudă, afaceri ilegale, spălare de bani, operațiuni bancare ilegale […]
• Serviciul de presă Banca Centrală a Federației Ruse (Banca Rusiei) Serviciul de presă 107016, Moscova, st. Neglinnaya, 12www.cbr.ru Cu privire la numirea unei administrații interimare, Departamentul pentru Relații Externe și Publice al Băncii Rusiei informează că, în conformitate cu paragraful 2 […]
• Caracteristici generale și o scurtă prezentare a căilor navigabile Clasificarea bazinelor de apă Clasificarea bazinelor de apă pentru navigarea ambarcațiunilor (mici) de agrement, supravegheată de GIMS din Rusia, se realizează în funcție de […]
• Kucherena = avocatul lui Viktor Tsoi Și acesta este un exclusiv: scrisoarea de astăzi de la Anatoly Kucherena. În continuarea subiectului. Nimeni nu a publicat încă această scrisoare. Și ar trebui, cred. Partea 1 pentru moment. În curând voi publica partea a doua, semnată de celebrul avocat. De ce este important? […]

Trebuie să faceți calcule complexe, dar nu avea la îndemână niciun dispozitiv de calcul electronic? Utilizați calculatorul de rădăcină online. Ea va ajuta:

• găsiți rădăcini pătrate sau cubice ale numerelor date;
• efectuați o operație matematică cu puteri fracționale.

Număr de zecimale:

√

Cum se calculează manual rădăcina pătrată - utilizați metoda de selecție pentru a găsi valori adecvate. Să vedem cum se face.

Ce este o rădăcină pătrată

Rădăcină n puterile unui număr natural A- număr, n al cărui grad este egal cu A(număr radical). Rădăcina este notată cu simbolul √. Ei îl numesc un radical.

Fiecare operație matematică are o reacție: adunare → scădere, înmulțire → împărțire, exponențiere → extracție rădăcină.

Rădăcina pătrată a unui număr A va fi un număr al cărui pătrat este egal cu A. De aici urmează răspunsul la întrebarea, cum se calculează rădăcina unui număr? Trebuie să alegeți un număr care la a doua putere va fi egal cu valoarea de sub rădăcină.

De obicei, 2 nu este scris deasupra semnului rădăcină. Deoarece aceasta este cea mai mică putere și, în consecință, dacă nu există un număr, atunci este implicat indicatorul 2. Decidem: pentru a calcula rădăcina pătrată a lui 16, trebuie să găsiți un număr care, atunci când este ridicat la a doua putere , va avea 16 ani.

Efectuăm calculele manual

Calculele prin factorizare în factori primi sunt efectuate în două moduri, în funcție de numărul rădăcinii:

1. Un număr întreg care poate fi factorizat în factori pătrați și poate obține răspunsul exact.

Numerele pătrate sunt numere care pot fi înrădăcinate fără rest. Factorii sunt numere care, atunci când sunt înmulțite, dau numărul inițial.

De exemplu:

25, 36, 49 sunt numere pătrate deoarece:

Se pare că factorii pătrați sunt factori care sunt numere pătrate.

Să luăm 784 și să extragem rădăcina din el.

Descompunem numărul în factori pătrați. Numărul 784 este un multiplu al lui 4, deci primul factor pătrat este 4 x 4 = 16. Împărțiți 784 la 16, obținem 49 - și acesta este un număr pătrat 7 x 7 = 16.
Aplica regula Luăm rădăcina fiecărui factor pătrat, înmulțim rezultatele și obținem răspunsul.	Răspuns.

2. Indivizibil. Nu poate fi descompus în factori pătrați.

Astfel de exemple sunt mai frecvente decât în ​​cazul numerelor întregi. Soluția lor nu va fi exactă, cu alte cuvinte întreagă. Va fi fracționat și aproximativ. Pentru a simplifica sarcina, va ajuta extinderea numărului rădăcinii într-un factor pătrat și un număr din care este imposibil să extrageți rădăcina pătrată.

Descompunem numărul 252 într-un pătrat și un factor regulat.
Evaluăm valoarea rădăcinii. Pentru a face acest lucru, selectăm două numere pătrate care sunt în fața și în spatele numărului radical din rigla digitală.	Numărul rădăcină este 7. Deci cel mai apropiat număr pătrat mai mare va fi 8, iar cel mai mic va fi 4. intre 2 si 4.
Evaluarea valorii	Cel mai probabil, √7 este mai aproape de 2. Îl selectăm în așa fel încât atunci când acest număr este înmulțit cu el însuși, obținem 7. 2,7 x 2,7 = 7,2. Nu este potrivit, deoarece 7,2>7, luăm cel mai mic 2,6 x 2,6 = 6,76. Plecăm, pentru că 6.76 ~ 7.
Calculați rădăcina

Cum se calculează rădăcina unui număr complex? De asemenea, prin metoda de estimare a valorilor rădăcinii.

La împărțirea într-o coloană, răspunsul cel mai precis este obținut la extragerea rădăcinii.

Luați o foaie de hârtie și trageți-o astfel încât linia verticală să fie în mijloc, iar linia orizontală să fie pe partea dreaptă și sub început.
Împărțiți numărul rădăcină în perechi de numere. Decimalele sunt împărțite astfel: - întreaga parte de la dreapta la stânga; este numărul după virgulă zecimală de la stânga la dreapta.	Exemplu: 3459842,825694 → 3 45 98 42, 82 56 94 795,28 → 7 95, 28 Este permis ca la început să existe un număr nepereche.
Pentru primul număr (sau pereche), selectăm cel mai mare număr n. Pătratul său trebuie să fie mai mic sau egal cu valoarea primului număr (perechea de numere). Luați rădăcina acestui număr - √n. Scrieți rezultatul obținut în dreapta sus, iar pătratul acestui număr - în dreapta jos. Avem primul 7. Cel mai apropiat număr pătrat este 4. Este mai mic decât 7 și 4 =
Scădeți pătratul găsit al numărului n din primul număr (pereche). Înregistrați rezultatul sub 7. Și dublați numărul de sus din dreapta și scrieți expresia 4_х_=_ în dreapta. Notă: numerele trebuie să fie aceleași.
Selectăm un număr pentru expresia cu liniuțe. Pentru a face acest lucru, găsiți un număr astfel încât produsul rezultat să nu fie mai mare sau egal cu numărul curent din stânga. În cazul nostru este 8.
Notați numărul găsit în colțul din dreapta sus. Acesta este al doilea număr de la rădăcina dorită. Demolați următoarea pereche de numere și scrieți lângă diferența rezultată din stânga.
Scădeți produsul din dreapta din numărul din stânga. Dublam numărul care se află în dreapta sus și scriem expresia cu liniuțe.
Mai demolăm câteva numere până la diferența rezultată. Dacă acestea sunt numere ale părții fracționale, adică sunt situate în spatele unei virgule, atunci punem o virgulă în colțul din dreapta sus, lângă ultima cifră a rădăcinii pătrate dorite. Completam liniuțele în expresia din dreapta, alegând un număr astfel încât produsul rezultat să fie mai mic sau egal cu diferența expresiei din stânga.
Dacă aveți nevoie de mai multe zecimale, adăugați în apropierea cifrei curente din stânga și repetați pașii: scădeți din stânga, dublați numărul din colțul din dreapta sus, scrieți expresia cu liniuțe, selectați factorii pentru ea și așa mai departe.

Cât timp crezi că vei petrece astfel de calcule? Dificil, lung, confuz. Atunci de ce să nu îți faci totul ușor? Utilizați programul nostru pentru a vă ajuta să faceți calcule rapide și precise.

Algoritm de acțiune

1. Introduceți numărul dorit de zecimale.

2. Precizați gradul rădăcinii (dacă este mai mare de 2).

3. Introduceți numărul din care intenționați să extrageți rădăcina.

4. Faceți clic pe butonul „Rezolvare”.

Calcularea celor mai complexe operații matematice cu un calculator online va fi ușor!.

Adunarea și scăderea rădăcinilor- una dintre cele mai frecvente „pietre de poticnire” pentru cei care urmează un curs de matematică (algebră) în liceu. Cu toate acestea, învățarea cum să le adunăm și să le scădem corect este foarte importantă, deoarece exemple pentru suma sau diferența de rădăcini sunt incluse în programul Examenului de stat unificat de bază la disciplina „matematică”.

Pentru a stăpâni soluția unor astfel de exemple, aveți nevoie de două lucruri - să înțelegeți regulile, precum și să obțineți practică. După ce a rezolvat una sau două duzini de exemple tipice, studentul va aduce această abilitate la automatism, iar apoi nu va avea de ce să se teamă la examen. Este recomandat să începeți să stăpâniți operațiile aritmetice cu adunare, deoarece adăugarea lor este puțin mai ușoară decât scăderea lor.

Ce este o rădăcină

Cel mai simplu mod de a explica acest lucru este cu exemplul unei rădăcini pătrate. În matematică, există un termen bine stabilit „pătrat”. „Pătrat” înseamnă a înmulți un anumit număr cu el însuși o dată.. De exemplu, dacă pătrați 2, obțineți 4. Dacă pătrați 7, obțineți 49. Pătratul lui 9 este 81. Deci rădăcina pătrată a lui 4 este 2, a lui 49 este 7 și a lui 81 este 9.

De regulă, predarea acestei teme în matematică începe cu rădăcini pătrate. Pentru a o determina imediat, un elev de liceu trebuie să cunoască pe de rost tabla înmulțirii. Pentru cei care nu cunosc bine acest tabel, trebuie să folosiți indicii. De obicei, procesul de extragere a pătratului rădăcină dintr-un număr este dat sub forma unui tabel pe coperțile multor caiete școlare de matematică.

Rădăcinile sunt de următoarele tipuri:

• pătrat;
• cubic (sau așa-numitul grad al treilea);
• gradul al patrulea;
• gradul cinci.

Reguli de adăugare

Pentru a rezolva cu succes un exemplu tipic, trebuie avut în vedere că nu toate numerele de rădăcină pot fi stivuite unele cu altele. Pentru a le putea pune împreună, trebuie aduse la un singur model. Dacă acest lucru nu este posibil, atunci problema nu are soluție. Astfel de probleme se găsesc adesea și în manualele de matematică ca un fel de capcană pentru elevi.

Adăugarea nu este permisă în teme când expresiile radicale diferă unele de altele. Acest lucru poate fi ilustrat cu un exemplu ilustrativ:

• elevul se confruntă cu sarcina: să adauge rădăcina pătrată a lui 4 și a lui 9;
• un elev neexperimentat care nu cunoaște regula scrie de obicei: „rădăcina lui 4 + rădăcina lui 9 \u003d rădăcina lui 13”.
• este foarte usor de demonstrat ca acest mod de rezolvare este gresit. Pentru a face acest lucru, trebuie să găsiți rădăcina pătrată a lui 13 și să verificați dacă exemplul este rezolvat corect;
• folosind un microcalculator, puteți determina că este de aproximativ 3,6. Acum rămâne de verificat soluția;
• rădăcina lui 4=2 și a lui 9=3;
• Suma a doi și trei este cinci. Astfel, acest algoritm de soluție poate fi considerat incorect.

Dacă rădăcinile au același grad, dar expresii numerice diferite, se scoate din paranteze și suma a două expresii radicale. Astfel, este deja extras din această sumă.

Algoritm de adunare

Pentru a rezolva corect cea mai simplă problemă, este necesar:

1. Determinați exact ce necesită adăugare.
2. Aflați dacă este posibil să adăugați valori unul altuia, ghidându-vă după regulile existente în matematică.
3. Dacă nu pot fi adăugate, trebuie să le transformați în așa fel încât să poată fi adăugate.
4. După ce au efectuat toate transformările necesare, este necesar să se efectueze adunarea și să noteze răspunsul final. Adăugarea se poate face mental sau cu un calculator, în funcție de complexitatea exemplului.

Care sunt rădăcini asemănătoare

Pentru a rezolva corect un exemplu de adăugare, este necesar, în primul rând, să ne gândim la modul în care poate fi simplificat. Pentru a face acest lucru, trebuie să aveți cunoștințe de bază despre asemănarea.

Capacitatea de a le identifica pe altele asemănătoare ajută la rezolvarea rapidă a aceluiași tip de exemple de adăugare, aducându-le într-o formă simplificată. Pentru a simplifica un exemplu tipic de adăugare, trebuie să:

1. Găsiți unele similare și alocați-le unui grup (sau mai multor grupuri).
2. Rescrie exemplul existent în așa fel încât rădăcinile care au același indicator să se succedă clar (aceasta se numește „grupare”).
3. În continuare, ar trebui să scrieți din nou expresia, de data aceasta în așa fel încât altele asemănătoare (care au același indicator și aceeași cifră rădăcină) să se sucească și ele.

După aceea, un exemplu simplificat este de obicei ușor de rezolvat.

Pentru a rezolva corect orice exemplu de adăugare, trebuie să înțelegeți clar regulile de bază ale adunării și, de asemenea, să știți ce este o rădăcină și cum se întâmplă.

Uneori, astfel de sarcini par foarte complicate la prima vedere, dar de obicei sunt rezolvate cu ușurință prin gruparea unora similare. Cel mai important lucru este practica, iar apoi studentul va începe să „face clic pe sarcini precum nucile”. Adunarea rădăcinilor este una dintre cele mai importante ramuri ale matematicii, așa că profesorii ar trebui să aloce suficient timp pentru a o studia.

Video

Acest videoclip vă va ajuta să înțelegeți ecuațiile cu rădăcini pătrate.