Что такое уравнение и в чем его смысл? Астрономические опыты Смотреть что такое "Уравнение времени" в других словарях

Уравнением времени называется разность между средним и истинным солнечным временем в один и тот же момент. Продолжительность истинных солнечных суток не одинакова в течение года, поскольку Солнце движется по эклиптике неравномерно. Из-за эксцентриситета земной орбиты зимой в северном полушарии сутки длятся немного больше, чем летом, а в южном – наоборот. Поэтому были введены средние солнечные сутки, равные 24 часам на протяжении всего года. Для определения понятия средних солнечных суток вводится дополнительное понятие «среднее Солнце» – фиктивная точка, которая равномерно движется по небесному экватору (не по эклиптике!) Уравнение времени позволяет переходить от истинного солнечного времени к среднему солнечному и наоборот.

Уравнение времени в авиационной астрономии используется для приближённого расчёта часового угла истинного Солнца, когда нет под рукой ААЕ по показаниям часов, идущих по среднему времени.

Определить поправку можно различными способами.

Графическое представление

Табличная форма

Аналитическое решение

η=7.8*sin(D-2)+10*sin(2D+10) , где

D=(d*360/365) - приращение долготы среднего Солнца от начала года;

d - порядковый номер дня в году.

Пример использования

Определим время истинного полдня на 1 ноября точки с восточной долготой 87 градусов в Северном полушарии, в часовом поясе +7 GMT. Для этого переведём долготу в меру времени. 15 градусов долготы соответствуют одному часу (360/24 часа). 87 градусов соответствуют 5 часам 48 минутам. Разница с поясным составит 1 час 12 минут.

Значит по местному среднему солнечному времени полдень будет не в 12 часов, а в 13:12 и плюс поправка на Уравнение времени.

Для 1 ноября поправка равна 16 минут. Определимся со знаком поправки. Вспоминаем что в северном полушарии зимой сутки длиннее (больше 24 часов). Значит настоящее Солнце движется быстрее "среднего" Солнца и полдень наступит раньше. Отнимаем поправку и узнаём, по обычным часам (а они показывают среднесолнечное время), что полдень наступит в 12:56

Аналемма

На практике также удобно пользоваться представлением уравнения времени в виде кривой, называемой аналемма . Она позволяет, кроме временной поправки, одновременно определять и склонение Солнца.

Аналемма является траекторией, соединяющей ряд последовательных положений Солнца на небосводе в одно и то же время в течение года. То есть, если фотографировать Солнце из одного места и в одно и то же время в течение года, то в зависимости от широты и выбранного времени, получится приблизительно такая картина:

Аналемма на фотографии

Уравнение времени, разность между средним и истинным солнечным временем; равна разности прямых восхождений истинного и среднего Солнца. Часто У. в. определяют как разность истинного и среднего времени; в этом случае оно имеет противоположный знак, что нужно иметь в виду при пользовании справочниками.

У. в. непрерывно меняется. Это обусловлено тем, что истинное солнечное время, измеряемое часовым углом истинного Солнца, течёт неравномерно вследствие, во-первых, неравномерности движения Земли по орбите и, во-вторых, наклона эклиптики к экватору. Поэтому У. в. получается в результате сложения двух волн приблизительно синусоидальной формы и почти равной амплитуды (см. рис. ). Одна из этих волн имеет годичный, другая – полугодичный периоды. Четыре раза в году, а именно: около 16 апреля, 14 июня, 1 сентября и 25 декабря У. в. равно нулю и достигает 4 раза наибольшего значения (по абсолютной величине): около 12 февраля + 14,3 мин, 15 мая – 3,8 мин, 27 июля + 6,4 мин и 4 ноября – 16,4 мин. С помощью У. в. может быть найдено среднее местное солнечное время, если известно истинное солнечное время, определённое по наблюдениям Солнца, например с помощью солнечных часов; при этом пользуются формулой:

m = m 0 + h ,

где m – среднее время, m 0 – истинное время, h – У. в. Значения У. в. на каждый день даются в астрономических ежегодниках и календарях. См. Время .

График уравнения времени: 1 - составляющая уравнения времени, определяемая неравномерностью движения Земли по орбите; 2 - составляющая уравнения времени, определяемая наклоном эклиптики к экватору; 3 - уравнение времени.

Большая Советская Энциклопедия М.: "Советская энциклопедия", 1969-1978

Уравнение времени

График уравнения времени (синяя линия) и двух его составляющих при определении этого уравнения как УВ = ССВ - ИСВ.

Уравнение времени - разница между средним солнечным временем (ССВ) и истинным солнечным временем (ИСВ), то есть УВ = ССВ - ИСВ . Эта разница в каждый конкретный момент времени одинакова для наблюдателя в любой точке Земли. Уравнение времени можно узнать из специализированных астрономических изданий, астрономических программ или вычислить по формуле, приведенной ниже.

В таких изданиях, как «Астрономический календарь», уравнение времени определяется как разность часовых углов среднего экваториального солнца и истинного солнца, то есть, при таком определении УВ = ССВ - ИСВ .

В англоязычных изданиях часто применяется иное определение уравнения времени (т.н. «инвертированное»): УВ = ИСВ - ССВ, то есть разница между истинным солнечным временем (ИСВ) и средним солнечным временем (ССВ).

Некоторые пояснения к определению

Можно встретить определение уравнения времени как разницы «местного истинного солнечного времени» и «местного среднего солнечного времени» (в англоязычной литературе - local apparent solar time и local mean solar time ). Данное определение формально более точно, но не влияет на результат, так как для любой конкретной точки на Земле эта разница одинакова.

Кроме того, не следует путать ни «местное истинное солнечное время», ни «местное среднее солнечное время» с поясным временем - временем «официальных» часов (например, «Московское время»).

Объяснение неравномерности движения истинного Солнца

В отличие от звезд, чьё видимое суточное движение практически равномерно и обусловлено только вращением Земли вокруг своей оси, суточное движение Солнца не равномерно, так как обусловлено и вращением Земли вокруг своей оси, и вращением Земли вокруг Солнца, и наклоном земной оси к плоскости эклиптики.

Неравномерность, обусловленная эллиптичностью орбиты

Вращение Земли вокруг Солнца происходит по эллиптической орбите. Согласно второму закону Кеплера , такое движение неравномерно, оно быстрее в области перигелия и медленнее в области афелия . Для наблюдателя, находящегося на Земле, это выражается в том, что видимое движение Солнца по эклиптике относительно неподвижных звезд то ускоряется, то замедляется.

Неравномерность обусловленная наклоном земной оси

Уравнение времени обращается в ноль четыре раза в году: 14 апреля , 14 июня , 2 сентября и 24 декабря .

Соответственно, в каждое время года существует свой максимум уравнения времени: около 12 февраля - +14,3 мин, 15 мая - −3,8 мин, 27 июля - +6,4 мин и 4 ноября - −16,4 мин. Точные величины уравнения времени даются в астрономических ежегодниках.

Может применяться как дополнительная функция в некоторых моделях часов .

Расчёт

Уравнение можно аппроксимировать отрезком ряда Фурье как сумму двух синусоидальных кривых с периодами, соответственно, на один год и шесть месяцев:

если углы выражаются в градусах. если углы выражаются в радианах. Там, где - количество дней, например: на 1 января на 2 января

Примечания

Ссылки

• Величина колебаний уравнения времени в течение года на портале Гринвичской королевской обсерватории .
• Образец построения графика уравнения времени , где прорисованы:

1 - составляющая уравнения времени, определяемая неравномерностью движения Земли по орбите, 2 - составляющая уравнения времени, определяемая наклоном эклиптики к экватору, 3 - уравнение времени.

Wikimedia Foundation . 2010 .

Смотреть что такое "Уравнение времени" в других словарях:

- (Equation of time) разность прямых восхождений истинного и среднего Солнца, или разность часовых углов среднего и истинного Солнца: Самойлов К. И. Морской словарь. М. Л.: Государственное Военно морское Издательство НКВМФ Союза ССР, 1941 Уравнение … Морской словарь

Разность между средним (среднеэкваториальным) солнечным временем и истинным солнечным временем. Изменяется в течение года от 16,4 мин до + 14,3 мин … Большой Энциклопедический словарь

уравнение времени - Разность между средним и истинным солнечным временем, плавно изменяющаяся в течение года от 16,4 до +14,3 мин … Словарь по географии

Разность между средним и истинным солнечным временем; равна разности прямых восхождений истинного и среднего Солнца. Часто У. в. определяют как разность истинного и среднего времени; в этом случае оно имеет противоположный знак, что нужно … Большая советская энциклопедия

Разность между средним солнечным временем и истинным солнечным временем. Изменяется в течение года от 16,4 мин до +14,3 мин. * * * УРАВНЕНИЕ ВРЕМЕНИ УРАВНЕНИЕ ВРЕМЕНИ, разность между средним (среднеэкваториальным) солнечным временем и истинным… … Энциклопедический словарь

См. Полдень … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Естествознание. Энциклопедический словарь

Разность между средним солнечным временем и истинным солнечным временем. Изменяется в течение года от 16,4 мин до +14,3 мин … Астрономический словарь

График уравнения времени (синяя линия) и двух его составляющих при определении этого уравнения как УВ = ССВ - ИСВ.

Уравнение времени - разница между средним солнечным временем (ССВ) и истинным солнечным временем (ИСВ), то есть УВ = ССВ - ИСВ . Эта разница в каждый конкретный момент времени одинакова для наблюдателя в любой точке Земли. Уравнение времени можно узнать из специализированных астрономических изданий, астрономических программ или вычислить по формуле, приведенной ниже.

В таких изданиях, как «Астрономический календарь», уравнение времени определяется как разность часовых углов среднего экваториального солнца и истинного солнца, то есть, при таком определении УВ = ССВ - ИСВ .

В англоязычных изданиях часто применяется иное определение уравнения времени (т. н. «инвертированное»): УВ = ИСВ - ССВ, то есть разница между истинным солнечным временем (ИСВ) и средним солнечным временем (ССВ).

Некоторые пояснения к определению

Можно встретить определение уравнения времени как разницы «местного истинного солнечного времени» и «местного среднего солнечного времени» (в англоязычной литературе - local apparent solar time и local mean solar time ). Данное определение формально более точно, но не влияет на результат, так как для любой конкретной точки на Земле эта разница одинакова.

Кроме того, не следует путать ни «местное истинное солнечное время», ни «местное среднее солнечное время» с официальным местным временем (standard time ).

Объяснение неравномерности движения истинного Солнца

В отличие от звёзд, чьё видимое суточное движение практически равномерно и обусловлено только вращением Земли вокруг своей оси, суточное движение Солнца не равномерно, так как обусловлено и вращением Земли вокруг своей оси, и обращением Земли вокруг Солнца, и наклоном земной оси к плоскости орбиты Земли.

Неравномерность, обусловленная эллиптичностью орбиты

Вращение Земли вокруг Солнца происходит по эллиптической орбите. Согласно второму закону Кеплера , такое движение неравномерно, оно быстрее в области перигелия и медленнее в области афелия . Для наблюдателя, находящегося на Земле, это выражается в том, что видимое движение Солнца по эклиптике относительно неподвижных звёзд то ускоряется, то замедляется.

Неравномерность, обусловленная наклоном земной оси

Уравнение времени обращается в ноль четыре раза в году: 14 апреля , 14 июня , 2 сентября и 24 декабря .

Соответственно, в каждое время года существует свой максимум уравнения времени: около 12 февраля - +14,3 мин, 15 мая - −3,8 мин, 27 июля - +6,4 мин и 4 ноября - −16,4 мин. Точные величины уравнения времени даются в астрономических ежегодниках.

Может применяться как дополнительная функция в некоторых моделях часов .

Расчёт

Уравнение можно аппроксимировать отрезком ряда Фурье как сумму двух синусоидальных кривых с периодами, соответственно, в один год и в шесть месяцев:

E = 7.53 cos ⁡ (B) + 1.5 sin ⁡ (B) − 9.87 sin ⁡ (2 B) {\displaystyle E=7.53\cos(B)+1.5\sin(B)-9.87\sin(2B)} B = 360 ∘ (N − 81) / 365 {\displaystyle B=360^{\circ }(N-81)/365} если углы выражаются в градусах. B = 2 π (N − 81) / 365 {\displaystyle B=2\pi (N-81)/365} если углы выражаются в радианах. Там, где N {\displaystyle N} - номер дня в году, например: N = 1 {\displaystyle N=1} на 1 января N = 2 {\displaystyle N=2} на 2 января

Программа расчета на Ruby для текущей даты

#!/usr/bin/ruby =begin Equation of Time calculation *** No guarantees are implied. Use at your own risk *** Written by E. Sevastyanov, 2017-05-14 Based on "Equation of time" WikiPedia article as of 2016-11-28 (which describes angles in a bewildering mixture of degrees and radians) and Del Smith, 2016-11-29 It appears to give a good result, but I make no claims for accuracy. =end pi = (Math :: PI ) # pi delta = (Time . now . getutc . yday - 1 ) # (Текущий день года - 1) yy = Time . now . getutc . year np = case yy #The number np is the number of days from 1 January to the date of the Earth"s perihelion. (http://www.astropixels.com/ephemeris/perap2001.html) when 2017 ; 3 when 2018 ; 2 when 2019 ; 2 when 2020 ; 4 when 2021 ; 1 when 2022 ; 3 when 2023 ; 3 when 2024 ; 2 when 2025 ; 3 when 2026 ; 2 when 2027 ; 2 when 2028 ; 4 when 2029 ; 1 when 2030 ; 2 else ; 2 end a = Time . now . getutc . to_a ; delta = delta + a [ 2 ]. to_f / 24 + a [ 1 ]. to_f / 60 / 24 # Поправка на дробную часть дня lambda = 23 . 4406 * pi / 180 ; # Earth"s inclination in radians omega = 2 * pi / 365 . 2564 # angular velocity of annual revolution (radians/day) alpha = omega * ((delta + 10 ) % 365 ) # angle in (mean) circular orbit, solar year starts 21. Dec beta = alpha + 0 . 033405601 88317 * Math . sin (omega * ((delta - np ) % 365 )) # angle in elliptical orbit, from perigee (radians) gamma = (alpha - Math . atan (Math . tan (beta ) / Math . cos (lambda ))) / pi # angular correction eot = (43200 * (gamma - gamma . round )) # equation of time in seconds puts "EOT =" + (- 1 * eot ) . to_s + " секунд"

Математическая сторона основной задачи строительной механики основана на зависимостях, полученных в сопромате. Напомним их на примере напряженно-деформированного состояния элемента рамы, для которого – в отличие от балки – поперечный изгиб сопровождается дополнительным растяжением или сжатием.

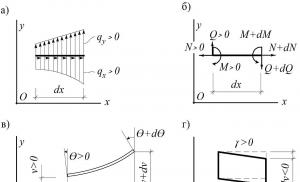
Пусть такой элемент длиной dx расположен в локальной системе координат Oxy , где ось Ox направлена по оси стержня, и загружен распределенной нагрузкой интенсивностью q x и q y вдоль Ox и Oy соответственно (рис. 1.20).

Напряженно-деформированное состояние стержня определяется девятью компонентами:

– внутренними усилиями (M , Q , N ,);

– перемещениями (u , v , q);

– деформациями (κ, g, e).

Уравнения для определения этих функций можно разделить на три группы.

Статические уравнения – связывают внутренние усилия (рис. 1.20, б ) с заданной нагрузкой:

dN /dx = – q x ; ü

dQ /dx = q y ; ý (1.10)

dM /dx = Q . þ

Геометрические уравнения – выражают деформации через перемещения, показанные на рис. 1.20, в , г :

κ = d q/dx ; ü

g = q - dv /dx ; ý (1.11)

e = du /dx . þ

Физические уравнения – представляют собой зависимости между внутренними усилиями и деформациями:

κ = M /EJ ; ü

g = mQ /GF ; ý (1.12)

e = N /EF ; þ

где E – модуль Юнга;

G – модуль сдвига;

F – площадь поперечного сечения стержня;

J – момент его инерции;

m – коэффициент, учитывающий неравномерность распределения касательных напряжений в поперечном сечении стержня.

Q > 0

γ>0

Q +dQ

M > 0

N +dN

q x > 0

q y > 0

u >0

θ>0

N > 0

M +dM

θ+d θ > 0

Отметим, что выражения EJ и EF в (1.12) называются жесткостями стержня при изгибе и растяжении (сжатии) соответственно.

При решении системы уравнений (1.10) – (1.12) возможны два варианта:

1) внутренние усилия M , Q , N удается найти из системы уравнений (1.10), не обращаясь к остальным уравнениям – это СОС;

2) внутренние усилия можно найти только путем совместного решения всех девяти уравнений – это СНС.

В последнем случае при решении этих уравнений возможны два подхода:

– в качестве основных неизвестных выбирают усилия M , Q , N , выражая все остальные через них – это решение в форме метода сил ;

– в качестве основных неизвестных выбирают перемещения u , v , q – это решение в форме метода перемещений .

Системы, описываемые линейными уравнениями (1.10) - (1.12), называются линейно-деформируемыми. Для них справедлив принцип суперпозиции , в соответствии с которым:

внутренние усилия, перемещения и деформации от заданной нагрузки (или иного воздействия) можно найти как сумму соответствующих величин от каждой нагрузки в отдельности.

Примечания

1. Первое из статических уравнений (1.10) получается из условия равновесия рассматриваемого элемента рамы. Полагая в его пределах q x = const, и составляя уравнение SX = 0, получим:

– N + q x ×dx + (N +dN ) = 0,

откуда и следует искомая зависимость. Два других уравнения из (1.10) – это дифференциальные зависимости Журавского .

2. Первое из физических уравнений (1.12) представляет собой дифференциальное уравнение изогнутой оси балки :

κ = d q/dx = d 2 v /dx 2 = M /EJ .

Второе уравнение в предпосылке равномерного распределения касательных напряжений в поперечном сечении стержня (m =1) выражает закон Гука при сдвиге :

t = Q /F = G g.

При этом мы не уточняем смысл коэффициента m по причине, которая будет указана в § 3.5. Последнее из физических уравнений (1.12) – это закон Гука при ЦРС :

s = N /F = E ×e.

3. В дальнейшем мы будет по-прежнему применять обозначение Oxy для глобальной системы координат, связанной с конструкцией в целом.