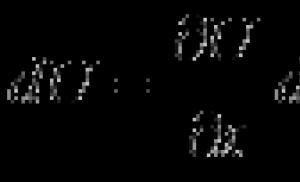Методические рекомендации на тему "метод координат". Метод координат в школьном курсе геометрии Этап. изучение новой темы

Метод координат

В тестах ЕГЭ задания части 1 (В 1 –В 14) и заданиях С 1 , С 2 являются стандартными с точки зрения школьной программы. Помимо заданий практико-ориентированного блока здесь предлагаются задачи на понимание основных фактов и идей школьного курса математики, а также задачи, где нужно решить уравнения, найти элементы пространственной фигуры, исследовать функцию и т.д. Для решения заданий С 2 необходим очень большой багаж знаний по геометрии, а также умение изображать пространственные фигуры на плоскости. Я остановлюсь только на одном виде решений задач С 2 . Это метод координат. Иногда он очень удобен для нахождения углов между плоскостями, между прямыми, между прямой и плоскостью и т.п. Для решения таких задач нам понадобятся уравнения плоскости и прямой.

1. а) Уравнение плоскости

где А (x 1 ; y 1 ; z 1), B (x 2 ; y 2 ; z 2), C (x 3 ; y 3 ; z 3) – точки данной плоскости.

б) Уравнение прямой

где M (x 1 ; y 1), N (x 2 ; y 2) – точки данной прямой.

Зная уравнения плоскостей, мы можем найти угол между ними по формуле

если α – угол между плоскостями

Зная уравнения прямых, мы можем найти угол между ними по формуле

если α – угол между прямыми с направляющими векторами) и).

Рассмотрим некоторые задания С 2 , где можно использовать метод координат.

Задача 1. В правильной четырехугольной призме ABCDA 1 B 1 C 1 D 1 . Стороны основания равны 3, а боковые ребра равны 5. На ребре DD 1 отмечена точка F так, что DF : FD 1 = 2:3. Найдите угол между плоскостями ADC и AFC 1 .

Введем прямоугольную систему координат. Вершины А (3; 0; 0); B (0; 0; 0); C (0; 3; 0) принадлежат плоскости (ABC ).

Можем составить уравнение этой плоскости.

Упростим и получим уравнение плоскости (ABC ):

Вершины А (3; 0; 0); F (3; 3; 2); C 1 (0; 3; 5) принадлежат плоскости (AFC 1). Можем составить уравнение этой плоскости.

упростим и получим уравнение.

Теперь найдем косинус угла между этими плоскостями

Часто ответы в этих задачах дают через тангенсы. Можно найти tgα по формуле; и.

Примечание: вычислить определитель третьего порядка можно по формуле

Можно эту формулу записать по-другому

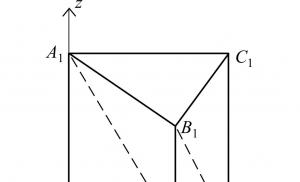
Задача 2. В правильной треугольной призме ABCA 1 B 1 C 1 сторона основания равна 2, высота равна 3. В треугольнике ABC проведена биссектриса AM . Найдите косинус угла между прямыми A 1 M и B 1 C .

Решение

Введем прямоугольную систему координат. Векторы и являются направляющими векторами прямых AC 1 и B 1 C . Найдем координаты этих векторов. Сначала находим координаты точек A 1 ; M ; B 1 ; C .

А 1 (0; 0; 3); B 1 (; 1; 3); С (0; 2; 0); M (; ; 0).

Теперь координаты направляющего вектора находим по следующему правилу: чтобы найти координаты вектора, надо из координат конца вычесть координаты начала . (; ; –3) и также (; 1; –3).

А теперь находим косинус угла между прямыми A 1 M и B 1 C по формуле

2. Рассмотрим формулу нахождения угла между прямой и плоскостью.

если α – угол между прямой и плоскостью

, (– направляющий вектор.

Задача 3. В прямоугольном параллелепипеде MNPQM 1 N 1 P 1 Q 1 ребра MN =15, MQ =MM 1 =8. Найдите угол между QP 1 и плоскостью QPN 1 .

Решение

Введем прямоугольную систему координат. Вектор направляющий для прямой QP 1 . Найдем его координаты.

Q (15; 8; 0); P 1 (0; 8; 8); (–15; 0; 8).

Теперь найдем уравнение плоскости (QPN 1).

Q (15; 8; 0); P (0; 8; 0); N (0; 0; 8).

Теперь найдем угол между и плоскостью

Задача 4. В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 высота равна 4, AB =4. Найдите угол между прямой AC 1 и плоскостью ACD 1 .

Решения

А (; –2; 0); C 1 (0; 4; 4); (; –6; 4).

Составим уравнение плоскости (ACD 1). А (; –2; 0); C (0; 4; 0); D 1 (; 6; 4).

Теперь найдем угол между прямой AC 1 и плоскостью (ACD 1).

Международный Университет природы, общества и человека «Дубна»

Проект программы по курсу

Разработка уроков по теме:

«Расстояние от точки до прямой»

«Расстояние между параллельными прямыми»

Дмитров, 2013 год

1. Введение…………………………………………………………………………………......…3

2. Проект программы по курсу

«Метод координат и основы аналитической геометрии на плоскости» ……………………………………………………………………………….......4

3. Разработка уроков:

Урок-лекция «Расстояние от точки до прямой»…………………….…...8

Урок-лекция «Расстояние между параллельными прямыми»…..17

4. Заключение……………………………………………………………………………………..23

5. Список литературы…………………………………………………………………………23

6. Приложения…………………………………………………………………………………….24

1.ВВЕДЕНИЕ

Стратегия развития современного общества на основе знаний и высокоэффективных технологий объективно требует внесения значительных корректив в педагогическую теорию и практику, активизации поиска новых моделей образования.

Изучение геометрии на ступени основного общего образова­ния направлено на достижение следующих целей:

- овладение системой знаний и умений , необ­ходимых для применения в практической деятельности, изу­чения смежных дисциплин, продолжения образования;

- интеллектуальное развитие , формирование качеств личности, необходимых человеку для полноценной жизни в современ­ном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;

- формирование представлений об идеях и методах математики как универсального языка науки и техники, средства модели­рования явлений и процессов;

- воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

В данном проекте изучение основ аналитической геометрии начинается с 7 класса , что позволит учащимся подойти к решению стереометрических задач с использованием метода координат на более осознанном и качественном уровне.

2.ОСНОВНАЯ ЧАСТЬ

Проект программы по курсу

«Метод координат и основы аналитической геометрии на плоскости»

для учащихся 7-8 классов основной школы

,

(Международный Университет природы, общества и человека «Дубна»)

и слушатели курсов ПК Международного университета «Дубна

1. Идея курса, цели и задачи –

Актуальность данной темы обусловлена тем, что используемые в основной школе содержание и методы преподавания математики в некоторой части не соответствуют современным потребностям подготовки специалистов в технических направлениях.

Цель : Приблизить содержание и методы преподавания математики в основной школе к современным потребностям технологического общества.

Задачи :

1. Проанализировать потребности современного технологического общества и сопоставить аппарат математики, используемый при решении прикладных задач с содержанием математики в основной школе.

2. Создание проекта программы по курсу «Метод координат и основы аналитической геометрии на плоскости»

3. Разработка уроков по теме «Расстояние от точки до прямой», «Расстояние между параллельными прямыми» р аздела «Взаимное расположение объектов на плоскости»

2. Место в программе общеобразовательной школы – 7-9 класс. Объем – 1 урок в неделю, параллельно с основным курсом традиционной геометрии, преподаваемой, например, по учебнику Атанасяна (с соавторами). Общий объём – 70 часов, что составляет 1/3 от общего объема курса по геометрии для 7-9 класса. Рекомендуемые сроки прохождения курса: начало – второе полугодие 7-го класса, окончание – 1-е полугодие 9-го класса. Однако в зависимости от конкретных условий освоения программы в каждой конкретной школе (учебные планы, рабочие программы, базовые учебники, наличие дополнительных часов в учебной сетке на геометрию) возможны другие сроки её освоения. Например, при наличии дополнительных часов срок освоения может быть сокращен за счет увеличения числа часов в неделю

3. Основные разделы и содержание.

Раздел		Часы
Второе полугодие 7 класса
1. Введение	Примеры задач и приложений.	1
2. Вектора на плоскости	Понятие вектора. Равенство векторов. Основные свойства и операции над векторами (сложение и вычитание векторов, умножение на число). Нулевой вектор. Вектора и геометрические фигуры. Самостоятельная работа.	4
3. Метод координат	Декартова прямоугольная система координат. Задание точек. Расстояние между точками (теорема Пифагора). Алгебраическое описание вектора. Операции над векторами, заданными в алгебраической форме. Алгебраическое описание многоугольников. Самостоятельная работа.	5
4. Скалярное произведение векторов	Угол между векторами. Проекция вектора на вектор. Скалярное произведение (аксиомы). Алгебраическое правило вычисления скалярного произведения. Определение косинуса и синуса угла на круге. Синус и косинусы простейших углов. Косинус угла между векторами и скалярное произведение векторов. Алгебраическое определение вида треугольника. Контрольная работа.	8
Первое полугодие 8 класса		17
5. Уравнение прямой на плоскости	Параметрическое уравнение прямой (два способа задания). Деление отрезка в заданном отношении. Описание многоугольников. Частные случаи уравнения прямой: каноническое и явное. Общее уравнение прямой. Геометрический смысл коэффициентов в общем уравнении прямой. Уравнение прямой в отрезках. Направляющие косинусы. Самостоятельная работа.	8
6. Взаимное расположение прямых на плоскости	Параллельность прямых на плоскости: формулировка критерия в зависимости от способа задания прямых. Построение прямой, параллельной данной и проходящей через заданную точку. Описание многоугольников с параллельными сторонами. Перпендикулярность прямых на плоскости: формулировка критерия в зависимости от способа задания прямых. Построение прямой, перпендикулярной данной и проходящей через заданную точку. Контрольная работа.	9
Второе полугодие 8 класса	18
7. Взаимное расположение объектов плоскости	Определение вида четырехугольника по координатам. Нахождении точек пересечения прямых. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Самостоятельная работа.	7
8. Симметрии плоскости	Центральная симметрия. Определение и примеры симметрий в простейших многоугольниках. Построение точек и прямых, симметричных данным относительно заданного центра симметрии (геометрическое построение и алгебраическое описание). Осевая симметрия. Определение и примеры симметрий в простейших многоугольниках. Построение точек и прямых, симметричным данным относительно оси симметрии (геометрическое построение и алгебраическое описание). Контрольная работа.	11
1 полугодие 9 класса		17
9. Особые точки и отрезки в простейших многоугольниках	Геометрическое построение точки пересечения медиан и его алгебраическое нахождение. Вычисление координат точек пересечения биссектрис, высот и серединных перпендикуляров. Их особые свойства. Самостоятельная работа.	6
10. Решение многоугольников	Решение задач по геометрии с использованием метода координат. Теорема косинусов. Контрольная работа.	6
11. Движение*, Повторение	Параллельный перенос, поворот	5

3.РАЗРАБОТКА УРОКОВ

Урок-лекция: «Расстояние от точки до прямой»

Цели: ввести понятия расстояния от точки до прямой, показать, как они применяются при решении задач.

1. Объяснение нового материала

Определение.

Расстояние от точки до прямой – это длина перпендикуляра, проведенного из данной точки к данной прямой

Следует обратить внимание на то, что расстояние от точки до прямой – это наименьшее из расстояний от этой точки до точек заданной прямой. Покажем это.

Возьмем на прямой a точку Q , не совпадающую с точкой M1 . Отрезок M1Q называют наклонной , проведенной из точки M1 к прямой a . Нам нужно показать, что перпендикуляр, проведенный из точки M1 к прямой a , меньше любой наклонной, проведенной из точки M1 к прямой a . Это действительно так: треугольник M1QH1 прямоугольный с гипотенузой M1Q , а длина гипотенузы всегда больше длины любого из катетов, следовательно, font-size:12.0pt;line-height:115%;font-family:Verdana">.

font-size:12.0pt; line-height:115%;font-family:Verdana">Если же при нахождении расстояния от точки до прямой есть возможность ввести прямоугольную систему координат, то можно воспользоваться методом координат. В этом уроке мы подробно остановимся на двух способах нахождения расстояния от точки M1 до прямой a , которые заданы в прямоугольной декартовой системе координат Oxy на плоскости. В первом случае расстояние от точки M1 до прямой a мы будем искать как расстояние от точки M1 до точки H1 , где H1 – основание перпендикуляра, опущенного из точки M1 на прямую a . Во втором способе нахождения расстояния от точки M1 до прямой a будем использовать нормальное уравнение прямой a .

Итак, поставим перед собой следующую задачу: пусть на плоскости зафиксирована прямоугольная система координат Oxy мы сможем вычислить, используя формулу для нахождения расстояния от точки M1 до точки H1 по их координатам: .

Осталось разобраться с нахождением координат точки H1 .

Мы знаем, что прямой линии в прямоугольной системе координат Oxy соответствует некоторо уравнение прямой на плоскости. Будем считать, что способ задания прямой a в условии задачи позволяет написать общее уравнение прямой a ил уравнение прямой с угловым коэффициентом. После этого мы можем составить уравнение прямой, проходящей через заданную точку М1, перпендикулярно прямой a . Обозначим эту прямую буквой b . Тогда точка H1 – это точка пересечения прямых a a и b , решая систему линейных уравнений font-size:12.0pt;line-height:115%;font-family:Verdana;color:#32322E">или ;

4) вычисляем требуемое расстояние от точки M1 до прямой a по формуле .

Сущность координатного метода для решения геометрических задач

Сущностью решения задач с помощью координатного метода состоит в том, чтоб ввести удобную нам в том или ином случае систему координат и переписать все данные с помощью него. После этого все неизвестные величины или доказательства проводятся с помощью этой системы. Как ввести координаты точек в любой системе координат, было нами рассмотрено в другой статье – здесь мы на этом останавливаться не будем.

Введем основные утверждения, которые используются в координатном методе.

Утверждение 1: Координаты вектора будут определяться разностью соответственных координат конца данного вектора и его же начала.

Утверждение 2: Координаты середины отрезка будут определяться как полусумма соответственных координат его границ.

Утверждение 3: Длина любого вектора $\overline{δ}$ с данными координатами $(δ_1,δ_2,δ_3)$ будет определяться формулой

$|\overline{δ}|=\sqrt{δ_1^2+δ_2^2+δ_3^2}$

Утверждение 4: Расстояние между двумя любыми точками, заданными координатами $(δ_1,δ_2,δ_3)$ и $(β_1,β_2,β_3)$ будет определяться формулой

$d=\sqrt{(δ_1-β_1)^2+(δ_2-β_2)^2+(δ_3-β_3)^2}$

Схема решения геометрических задач с использованием координатного метода

Для решения геометрических задач с помощью координатного метода лучше всего пользоваться данной схемой:

Провести анализ того, что дано в задаче:

• Задать наиболее подходящую для задачи систему координат;
• Математически записывается условие задачи, вопрос задачи, строится чертеж по данной задаче.

1. Все данные задачи записать в координатах выбранной системы координат.

2. Составить необходимые соотношения из условия задачи, а также связать эти соотношения с тем, что необходимо найти (доказать в задаче).
3. Полученный результат перевести на язык геометрии.

Примеры задач, решаемые координатным методом

Основными задачами, приводящими к координатному методу можно выделить следующие задачи (их решения здесь приводить не будем):

1. Задачи на нахождение координат вектора по его концу и началу.
2. Задачи, связанные с делением отрезка в каком-либо отношении.
3. Доказательство того, что три точки лежат на одной прямой или, что четыре точки лежат в одной плоскости.
4. Задачи на нахождение расстояния между двумя данными точками.
5. Задачи на нахождение объемов и площадей геометрических фигур.

Результаты решения первой и четвертой задачи приведены нами как основные утверждения выше и довольно часто используются для решения других задач с помощью координатного метода.

Примеры задач на применение метода координат

Пример 1

Найти боковую сторону правильной пирамиды, у которого высота равняется $3$ см, если сторона основания равняется $4$ см.

Пусть нам дана правильная пирамида $ABCDS$, высота которой – $SO$. Введем систему координат, как на рисунке 1.

Так как точка $A$ - центр построенной нами системы координат, то

Так как точки $B$ и $D$ принадлежат осям $Ox$ и $Oy$, соответственно, то

$B=(4,0,0)$, $D=(0,4,0)$

Так как точка $C$ принадлежит плоскости $Oxy$, то

Так как пирамида правильная, то $O$ - середина отрезка $$. По утверждению 2, получаем:

$O=(\frac{0+4}{2},\frac{0+4}{2},\frac{0+0}{2})=(2,2,0)$

Так как высота $SO$

Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:

На первый взгляд, выглядит угрожающе, но достаточно немного практики - и все будет работать великолепно.

Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).

Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:

Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.

Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат - точку (0; 0; 0) - то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;

Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.

Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.

Решение. Используя третью формулу, получаем n = (7; − 2; 4) - вот и все!

Вычисление координат векторов

А что, если в задаче нет векторов - есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек - начала и конца вектора - можно вычислить координаты самого вектора.

Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.

Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:

Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.

Рассмотрим вектор AB: его начало находится в точке A, а конец - в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).

Аналогично, начало вектора AC - все та же точка A, зато конец - точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).

Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).

Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)

Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!

Вычисление направляющих векторов для прямых

Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.

Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую...

Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый направляющий вектор для прямой:

Зачем нужен этот вектор? Дело в том, что угол между двумя прямыми - это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:

Задача. В кубе ABCDA 1 B 1 C 1 D 1 проведены прямые AC и BD 1 . Найдите координаты направляющих векторов этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA 1 соответственно. Единичный отрезок равен AB = 1.

Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) - это и есть направляющий вектор.

Теперь разберемся с прямой BD 1 . На ней также есть две точки: B = (1; 0; 0) и D 1 = (0; 1; 1). Получаем направляющий вектор BD 1 = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ: AC = (1; 1; 0); BD 1 = (− 1; 1; 1)

Задача. В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, проведены прямые AB 1 и AC 1 . Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA 1 , ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.

Для начала разберемся с прямой AB 1 . Тут все просто: у нас есть точки A = (0; 0; 0) и B 1 = (1; 0; 1). Получаем направляющий вектор AB 1 = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор для AC 1 . Все то же самое - единственное отличие в том, что у точки C 1 иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:

Ответ: AB 1 = (1; 0; 1);

Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.

Вычисление нормальных векторов для плоскостей

Нормальные векторы - это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости - это вектор, перпендикулярный данной плоскости.

Другими словами, нормаль - это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение - правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом - хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D - некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором - той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно - и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

Задача. В кубе ABCDA 1 B 1 C 1 D 1 проведено сечение A 1 BC 1 . Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA 1 соответственно.

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A 1 , B и C 1 , то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C 1 = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

Задача. В кубе ABCDA 1 B 1 C 1 D 1 проведено сечение AA 1 C 1 C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA 1 соответственно.

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A 1 и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A 1 = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 - без ущерба для общности решения и правильности ответа.

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами - точками A = (x a ; y a ; z a) и B = (x b ; y b ; z b). Тогда координаты середины отрезка - обозначим ее точкой H - можно найти по формуле:

Другими словами, координаты середины отрезка - это среднее арифметическое координат его концов.

Задача. Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Точка K - середина ребра A 1 B 1 . Найдите координаты этой точки.

Поскольку точка K - середина отрезка A 1 B 1 , ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A 1 = (0; 0; 1) и B 1 = (1; 0; 1). Теперь найдем координаты точки K:

Задача. Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A 1 B 1 C 1 D 1 .

Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A 1 L = C 1 L, т.е. точка L - это середина отрезка A 1 C 1 . Но A 1 = (0; 0; 1), C 1 = (1; 1; 1), поэтому имеем:

Ответ : L = (0,5; 0,5; 1)

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

Учебный комплекс авторской физико-математической школы-лицея № 61. ПРОЕКТ «Метод координат в математике и географии» Выполнили: учащиеся 7 Б и 7 В классов УК АФМШЛ № 61 Евлашков Даниил Литтау Роман Хегай Владимир Руководитель: Горборукова Н.В. г. Бишкек – 2012 г.

2 слайд

Описание слайда:

Определение местоположения того или иного предмета на поверхности Земли или какой-либо точки на плоскости – это определение их адреса. «Адрес» в географии – географическая широта; географическая долгота; абсолютная высота. «Адрес» в математике – абсцисса, ордината точки на координатной плоскости

3 слайд

Описание слайда:

Цель проекта: Исследовать и сравнить способы определения «адреса» объекта в географии и математики.

4 слайд

Описание слайда:

Задачи проекта: Ответить на следующие вопросы: Кто, когда и для чего впервые ввел понятие «координаты»? Существует ли генетическая связь между понятиями «географические координаты» и «координатный метод» в математике? Или это слова-омонимы? На развитие каких наук оказал влияние метод координат? Какие еще виды систем координат помимо прямоугольной существуют и используются человеком в настоящее время в практической деятельности?

5 слайд

Описание слайда:

Историческая справка. Во II – III веках до н. э. меридианы и параллели впервые появились на карте Эратосфена. Однако, они еще не представляли собой координатной сетки.

6 слайд

Описание слайда:

7 слайд

Описание слайда:

Во II в. до н. э. Гиппарх впервые разделил круг на 360 частей и предложил опоясать на карте Земной шар меридианами и параллелями. Ввел понятие – экватор, провел параллели и через полюса провел меридианы. Таким образом, была создана картографическая сеть и стало возможным наносить на карту географические объекты.

8 слайд

Описание слайда:

9 слайд

Описание слайда:

Завершил плеяду великих античных астрономов и географов Клавдий Птолемей (190 – 168 г.г. до н. э.). В своем труде «Руководство по географии» в 8 книгах дал описание свыше 8000 географических объектов с указанием их географических координат: широты и долготы.

10 слайд

Описание слайда:

1. География: «geo» – Земля, «grafo» – пишу. 2. Геометрия: «geo» – земля, «metreo» - измерять. Как видно, эти две науки были тесно связаны между собой, их возникновение обусловлено практической деятельностью людей того времени.

11 слайд

Описание слайда:

Почему географические широта и долгота измеряются в градусах? Географическая широта – это величина дуги меридиана от экватора до заданной точки. Из курса геометрии известно, что дуги измеряются как в линейных величинах, так и в угловых: градусах и радианах. Географическая долгота – это величина дуги параллели от нулевого меридиана до заданной точки. Видно, что географические координаты – понятие математическое.

12 слайд

Описание слайда:

Появление алгебры, как ветви математики. В IX веке узбекский математик и астроном Мухаммед аль-Хорезми пишет трактат «Китаб аль-джебр валь-мукабала» , где дал общие правила для решения уравнений 1 степени. Слово «аль-джебр» («восстановление») означало перенос отрицательных членов уравнений из одной его части в другую с изменением знака. От него новая наука получила свое название – алгебра. Долгое время алгебра и геометрия развивались параллельно и представляли собой две ветви математики.

13 слайд

Описание слайда:

В XIV в. французский математик Никола Орезм предложил ввести, по аналогии с географическими, координаты на плоскости. Он предложил покрыть плоскость прямоугольной сеткой и называть широтой и долготой то, что мы теперь называем абсциссой и ординатой. Это положило начало созданию метода координат и связало алгебру и геометрию.

14 слайд

Описание слайда:

Метод координат Алгебра Точка плоскости задается парой чисел М (x;y) - алгебраический объект Прямая линия задается уравнением у=ах+в Геометрия Точка плоскости - геометрический объект

15 слайд

Описание слайда:

Рене Декарт (1596-1650) – французский математик, философ, физик и физиолог. Декарт является одним из создателей аналитической геометрии, современной алгебраической символики, а метод задания кривой с помощью уравнения был решающим шагом к понятию функции. В математике именно ему принадлежит основная заслуга в создании метода координат, который был положен в основу аналитической геометрии.

16 слайд

Описание слайда:

1. Нужно отметить, что у Декарта еще не было того, что мы сегодня называем Декартовой системой координат. Декарт начал с того, что перевел на алгебраический язык задачи на построение циркулем и линейкой. 2. Немалой заслугой Декарта было введение удобных обозначений, используемых сегодня: x, y, z – для неизвестных, a, b, с - для коэффициентов, а также обозначение степеней. 3. В настоящее время декартовы координаты представляют собой ортогональные оси с одинаковым масштабом по всем направлениям, т.О является началом координат.

17 слайд

Описание слайда:

Сравним системы координат в математике и географии. 1. Для определения положения объекта на поверхности Земли необходимы 2 координаты: долгота и широта. 2. Для определения положения точки на плоскости необходимы 2 координаты: абсцисса и ордината. 3. Параллели и меридианы взаимно перпендикулярны. 4. Оси OX и OY взаимно перпендикулярны. 5. Для определения точки в пространстве требуется 3 – я координата: абсолютная высота (в географии); аппликата в математике. 6. Экватор и нулевой меридиан делят поверхность земного шара на 4 части 7. Координатные оси делят плоскость на 4 части, а пространство на 8 частей.

18 слайд

Описание слайда:

Полярные и сферические координаты. Полярная система координат включает в себя т.О – полюс и луч – полярную ось. Каждой точке на плоскости соответствует пара чисел Р(r; ф), угол между направлением на объект и полярной осью и расстояние до объекта В географии аналогом полярных координат является азимут. Для определения местоположения объекта требуется знать угол между направлением на предмет и направлением на север и расстояние до объекта.

19 слайд

Описание слайда:

Сферической системой координат пользуются, если необходимо определить положение точки в пространстве. Этот метод используется в аэронавигации. С помощью радара определяют 3 координаты: кратчайшее расстояние по прямой до самолета; угол, под которым самолет виден над горизонтом; угол между направлением на самолет и направлением на север

20 слайд

Описание слайда:

КОНЦЕПТУАЛЬНАЯ КАРТА География Картография Система координат 1. Прямоугольные - географическая широта - географическая долгота - абсолютная высота 2. Полярные - азимут - расстояние до объекта - абсолютная высота Математика Алгебра Геометрия Метод координат 1. Прямоугольные - абсцисса - ордината - аппликата 2. Полярные - угол поворота - расстояние от начала координат до точки

21 слайд