Acasă » clasa a 3-a » Care este sinusul lui 3x? Formule de bază ale trigonometriei. Formule trigonometrice de bază

Care este sinusul lui 3x? Formule de bază ale trigonometriei. Formule trigonometrice de bază

|BD| - lungimea arcului de cerc cu centrul în punctul A.
α este unghiul exprimat în radiani.

Tangenta ( tan α) este o funcție trigonometrică în funcție de unghiul α dintre ipotenuză și catetul unui triunghi dreptunghic, egal cu raportul dintre lungimea catetului opus |BC| la lungimea piciorului adiacent |AB| .
Cotangent ( ctg α) este o funcție trigonometrică în funcție de unghiul α dintre ipotenuză și catetul unui triunghi dreptunghic, egal cu raportul dintre lungimea catetei adiacente |AB| la lungimea piciorului opus |BC| .

Tangentă

Unde n- întreg.

În literatura occidentală, tangenta se notează după cum urmează:
.
;
;
.

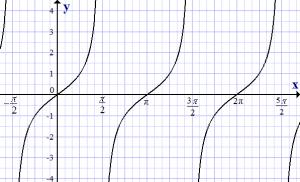
Graficul funcției tangente, y = tan x

Cotangentă

Unde n- întreg.

În literatura occidentală, cotangenta este desemnată după cum urmează:
.
De asemenea, sunt acceptate următoarele notații:
;
;
.

Graficul funcției cotangente, y = ctg x

Proprietățile tangentei și cotangentei

Periodicitate

Funcțiile y = tg xși y = ctg x sunt periodice cu perioada π.

Paritate

Funcțiile tangentă și cotangentă sunt impare.

Domenii de definire și valori, în creștere, în scădere

Funcțiile tangentă și cotangentă sunt continue în domeniul lor de definire (vezi dovada continuității). Principalele proprietăți ale tangentei și cotangentei sunt prezentate în tabel ( n- întreg).

	y = tg x	y = ctg x
Domeniul de aplicare și continuitatea
Gama de valori	-∞ < y < +∞	-∞ < y < +∞
Crescând		-
Descendentă	-
Extreme	-	-
Zerouri, y = 0
Interceptarea punctelor cu axa ordonatelor, x = 0	y = 0	-

Formule

Expresii folosind sinus și cosinus

; ;
; ;
;

Formule pentru tangentă și cotangentă din sumă și diferență

Formulele rămase sunt ușor de obținut, de exemplu

Produsul tangentelor

Formula pentru suma și diferența tangentelor

Acest tabel prezintă valorile tangentelor și cotangentelor pentru anumite valori ale argumentului.

Expresii folosind numere complexe

Expresii prin funcții hiperbolice

;
;

Derivate

; .

.
Derivată de ordinul n-a față de variabila x a funcției:
.
Derivarea formulelor pentru tangentă > > > ; pentru cotangent >>>

Integrale

Extinderi de serie

Pentru a obține expansiunea tangentei în puterile lui x, trebuie să luați mai mulți termeni ai expansiunii într-o serie de puteri pentru funcții sin xȘi cos xși împărțiți aceste polinoame între ele, . Aceasta produce următoarele formule.

La .

la .
Unde Bn- Numerele Bernoulli. Ele sunt determinate fie din relația de recurență:
;
;
Unde .
Sau conform formulei lui Laplace:

Funcții inverse

Funcțiile inverse ale tangentei și cotangentei sunt arctangente și, respectiv, arccotangente.

Arctangent, arctg

, Unde n- întreg.

Arccotangent, arcctg

, Unde n- întreg.

Referinte:
ÎN. Bronstein, K.A. Semendyaev, Manual de matematică pentru ingineri și studenți, „Lan”, 2009.
G. Korn, Manual de matematică pentru oameni de știință și ingineri, 2012.

Vezi si:

Puteți comanda o soluție detaliată la problema dvs.!!!

Formulele cu unghi dublu fac posibilă exprimarea funcțiilor trigonometrice (sinus, cosinus, tangentă, cotangentă) ale unghiului `2\alpha` prin chiar aceste funcții ale unghiului `\alpha`.

Lista de mai jos este formulele de bază ale unghiului dublu cel mai frecvent utilizate în trigonometrie. Pentru cosinus sunt trei dintre ele, toate sunt echivalente și la fel de importante.

`sin \ 2\alpha=` `2 \ sin \ \alpha \ cos \ \alpha`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha`, ` cos \ 2\alpha=1-2 \ sin^2 \alpha`, `cos \ 2\alpha=2 \ cos^2 \alpha-1`
`tg \ 2\alpha=\frac(2 \ tg \ \alpha)(1-tg^2 \alpha)`
`ctg \ 2\alpha=\frac(ctg^2 \alpha-1)(2 \ ctg \ \alpha)`

Următoarele identități exprimă toate funcțiile trigonometrice ale unghiului `2\alpha` prin funcțiile tangentă și cotangentă ale unghiului `\alpha`.

`sin \ 2\alpha=` `\frac (2 \ tg \ \alpha)(1+tg^2 \alpha)=\frac (2 \ ctg \ \alpha)(1+ctg^2 \alpha)=` `\frac 2(tg \ \alpha+ctg \ \alpha)`
`cos\2\alpha=` `\frac(1-tg^2\alpha)(1+tg^2\alpha)=\frac(ctg^2\alpha-1)(ctg^2\alpha+1) =` `\frac(ctg \ \alpha-tg \ \alpha)(ctg \ \alpha+tg \ \alpha)`
`tg \ 2\alpha=` `\frac(2 \ctg \ \alpha)(ctg^2 \alpha-1)=` `\frac 2(\ctg \ \alpha-tg \ \alpha)`
`ctg \ 2\alpha=\frac ( \ ctg \ \alpha-tg \ \alpha)2`

Formulele pentru cosinus și sinus ale unui unghi dublu funcționează pentru orice unghi `\alpha`. Formulele pentru tangentei unui unghi dublu sunt valabile pentru acele `\alpha` pentru care este definit `tg\2\alpha`, adică pentru ` \alpha\ne\frac\pi4+\frac\pi2 n, \n \în Z`. În mod similar, pentru cotangentă ele apar pentru acele `\alpha` pentru care este definită `ctg \2\alpha`, adică pentru ` \alpha\ne\frac\pi2 n, \n \in Z`.

Dovada formulelor cu unghi dublu

Toate formulele unghiului dublu sunt derivate din formulele pentru suma și diferența de unghiuri ale funcțiilor trigonometrice.

Să luăm două formule pentru suma unghiurilor sinusului și cosinusului:

`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta` și `cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`. Luați `\beta=\alpha`, apoi `sin(\alpha+\alpha)=` `sin \ \alpha\ cos \ \alpha+cos \ \alpha\ sin \ \alpha=2 \ sin \ \alpha \cos \ \alpha`, similar cu `cos(\alpha+\alpha)=` `cos \ \alpha\ cos \ \alpha-sin \ \alpha\ sin \ \alpha=cos^2 \alpha-sin^2 \alpha`, care și demonstrează formule cu unghi dublu pentru sinus și cosinus.

Alte două egalități pentru cosinusul ` cos \ 2\alpha=1-2 \ sin^2 \alpha ` și ` cos \ 2\alpha=2 \ cos^2 \alpha-1` sunt reduse la ceea ce a fost deja dovedit dacă înlocuim 1 în ele cu `sin^2 \alpha+cos^2 \alpha=1`. Deci `1-2 \sin^2 \alpha=` `sin^2 \alpha+cos^2 \alpha-2 \sin^2 \alpha=` `cos^2 \alpha-sin^2 \alpha` și ` 2 \cos^2 \alpha-1=` `2 \cos^2 \alpha-(sin^2 \alpha+cos^2 \alpha)=` `cos^2 \alpha-sin^2 \alpha`.

Pentru a demonstra formulele pentru tangentei unui unghi dublu și cotangentei, vom folosi definiția acestor funcții. Să scriem `tg \ 2\alpha` și `ctg \ 2\alpha` ca `tg \ 2\alpha=\frac (sin \ 2\alpha)(cos \ 2\alpha)` și `ctg \ 2\alpha= \frac (cos\2\alpha)(sin\2\alpha)`. Aplicând formulele deja dovedite de unghi dublu pentru sinus și cosinus, obținem `tg\2\alpha=\frac (sin\2\alpha)(cos\2\alpha)=\frac (2\sin\\alpha\cos\ \alpha )(cos^2 \alpha-sin^2 \alpha)` și `ctg \ 2\alpha=\frac (cos \ 2\alpha)(sin \ 2\alpha)=` `\frac (cos^2 \alpha -sin^2 \alpha)(2 \ sin \ \alpha \cos \ \alpha)`.

În cazul tangentei, împărțim numărătorul și numitorul fracției finale la `cos^2 \alpha`, pentru cotangente, la rândul său, la `sin^2 \alpha`.

`tg \ 2\alpha=\frac (sin \ 2\alpha)(cos \ 2\alpha)=\frac (2 \ sin \ \alpha \ cos \ \alpha)(cos^2 \alpha-sin^2 \ alpha)=` \frac (\frac(2 \ sin \ \alpha \ cos \ \alpha)(cos^2 \alpha))(\frac(cos^2 \alpha-sin^2 \alpha)(cos^ 2 \alpha))=` `\frac (2 \cdot \frac( sin \alpha )(cos \alpha))(1-\frac(sin^2 \alpha)(cos^2 \alpha))=\frac ( 2\tg\\alpha)(1-tg^2 \alpha)`.

`ctg \ 2\alpha=\frac (cos \ 2\alpha)(sin \ 2\alpha)=` `\frac (cos^2 \alpha-sin^2 \alpha)(2 \ sin \ \alpha \ cos \ \alpha)=` `\frac (\frac(cos^2 \alpha-sin^2 \alpha)(sin^2 \alpha))(\frac(2 \ sin \ \alpha \cos \ \alpha)( sin^2 \alpha))=` `\frac (\frac(cos^2 \alpha)(sin^2 \alpha)-1)(2 \cdot \frac(cos \alpha)( sin \alpha ))= \frac(ctg^2 \alpha-1)(2 \ctg \ \alpha)`.

De asemenea, vă recomandăm să vizionați videoclipul pentru a consolida mai bine materialul teoretic:

Exemple de utilizare a formulelor pentru rezolvarea problemelor

Formulele cu unghi dublu sunt cel mai adesea folosite pentru a converti expresii trigonometrice. Să ne uităm la câteva dintre cazuri și la modul în care acestea pot fi aplicate în practică atunci când rezolvăm probleme specifice.

Exemplul 1. Verificați validitatea identităților unghiului dublu pentru `\alpha=30^\circ`.

Soluţie. Formulele noastre folosesc două unghiuri `\alpha` și `2\alpha`. Valoarea primului unghi este specificată în condiție, al doilea în consecință va fi `2\alpha=60^\circ`. De asemenea, cunoaștem valorile numerice pentru toate funcțiile trigonometrice ale acestor unghiuri. Să le scriem:

`sin 30^\circ=\frac 1 2`, `cos 30^\circ=\frac (\sqrt 3)2`, `tg 30^\circ=\frac (\sqrt 3)3`, `ctg 30 ^\circ=\sqrt 3` și

`sin 60^\circ=\frac (\sqrt 3)2`, `cos 60^\circ=\frac 1 2`, `tg 60^\circ=\sqrt 3`, `ctg 60^\circ=\ frac (\sqrt 3)3`.

Atunci vom avea

`sin 60^\circ=2 sin 30^\circ cos 30^\circ=` `2 \cdot \frac 1 2 \cdot \frac (\sqrt 3)2=\frac (\sqrt 3)2`,

`cos 60^\circ=cos^2 30^\circ-sin^2 30^\circ=` `(\frac (\sqrt 3)2)^2 \cdot (\frac 1 2)^2=\frac 1 2`,

`tg 60^\circ=\frac(2 tg 30^\circ)(1-tg^2 30^\circ)=` `\frac(2 \cdot \frac (\sqrt 3)3)(1-( \frac (\sqrt 3)3)^2)=\sqrt 3`,

`ctg 60^\circ=\frac(ctg^2 30^\circ-1)(2 \ctg 30^\circ)=` `\frac((\sqrt 3)^2-1)(2 \cdot \ sqrt 3)=\frac (\sqrt 3)3`.

Ceea ce demonstrează validitatea egalităților pentru unghiul specificat în condiție.

Exemplul 2. Exprimați `sin \frac (2\alpha)3` în termeni de funcții trigonometrice ale unghiului `\frac (\alpha)6`.

Soluţie. Să scriem unghiul sinusoidal astfel: ` \frac (2\alpha)3=4 \cdot \frac (\alpha)6`. Apoi, aplicând formula unghiului dublu de două ori, ne putem rezolva problema.

În primul rând, vom folosi egalitatea sinusului unghiului dublu: ` sin\frac (2\alpha)3=2 \cdot sin\frac (\alpha)3 \cdot cos\frac (\alpha)3 `, acum vom aplica din nou formulele noastre pentru sinus și, respectiv, cosinus. Ca rezultat obținem:

` sin\frac (2\alpha)3=2 \cdot sin\frac (\alpha)3 \cdot cos\frac (\alpha)3=` `2 \cdot (2 \cdot sin\frac (\alpha)6 \cdot cos\frac (\alpha)6) \cdot (cos^2\frac (\alpha)6-sin^2\frac (\alpha)6)=` `4 \cdot sin\frac (\alpha)6 \cdot cos^3 \frac (\alpha)6-4 \cdot sin^3\frac (\alpha)6 \cdot cos \frac (\alpha)6`.

Răspuns. ` sin\frac (2\alpha)3=` `4 \cdot sin\frac (\alpha)6 \cdot cos^3 \frac (\alpha)6-4 \cdot sin^3\frac (\alpha)6 \cdot cos \frac (\alpha)6`.

Formule cu trei unghiuri

Aceste formule, similare celor anterioare, fac posibilă exprimarea funcțiilor unghiului `3\alpha` prin aceleași funcții ale unghiului `\alpha`.

`sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`
`tg \ 3\alpha=\frac(3 \ tg \ \alpha-tg^3 \alpha)(1-3 \ tg^2 \alpha)`
`ctg \ 3\alpha=\frac(ctg^3 \alpha-3 \ ctg \ \alpha)(3 \ ctg^2 \alpha-1)`

Ele pot fi dovedite folosind egalități de sumă și diferențe de unghi, precum și formulele unghiului dublu care ne sunt bine cunoscute.

`sin \ 3\alpha= sin (2\alpha+ \alpha)=` `sin 2\alpha cos \alpha+cos 2\alpha sin \alpha=` `2 sin \alpha cos \alpha cos \alpha+(cos^2 \alpha-sin^2 \alpha) sin \alpha=` `3 sin \alpha cos^2 \alpha-sin^3 \alpha`.

În formula rezultată, înlocuiți `sin \ 3\alpha=3 sin \alpha cos^2 \alpha-sin^3 \alpha` `cos^2\alpha` cu `1-sin^2\alpha` și obțineți `sin \ 3 \alpha=3 \sin \ \alpha-4sin^3 \alpha`.

De asemenea, pentru cosinusul unui unghi triplu:

`cos \ 3\alpha= cos (2\alpha+ \alpha)=` `cos 2\alpha cos \alpha-sin 2\alpha sin \alpha=` `(cos^2 \alpha-sin^2 \alpha) cos \alpha-2 sin \alpha cos \alpha sin \alpha+=` `cos^3 \alpha-3 sin^2 \alpha cos \alpha`.

Înlocuind `cos \ 3\alpha=cos^3 \alpha-3 sin^2 \alpha cos \alpha` `sin^2\alpha` în egalitatea finală cu `1-cos^2\alpha`, obținem `cos \ 3 \alpha=4cos^3 \alpha-3 \cos \ \alpha`.

Folosind identitățile dovedite pentru sinus și cosinus, putem demonstra pentru tangentă și cotangentă:

`tg \ 3\alpha=\frac (sin \ 3\alpha)(cos \ 3\alpha)=` `\frac (3 sin \alpha cos^2 \alpha-sin^3 \alpha)(cos^3 \ alpha-3 sin^2 \alpha cos \alpha)=` `\frac (\frac(3 sin \alpha cos^2 \alpha-sin^3 \alpha)(cos^3 \alpha))(\frac(cos ^3 \alpha-3 sin^2 \alpha cos \alpha)(cos^3 \alpha))=` `\frac (3 \cdot \frac( sin \alpha )(cos \alpha)-\frac( sin^ 3 \alpha )(cos^3 \alpha))(1-3\frac(sin^2 \alpha)(cos^2 \alpha))=` `\frac(3 \ tg \ \alpha-tg^3 \ alfa)(1-3tg^2 \alpha)`;

`ctg \ 3\alpha=\frac (cos \ 3\alpha)(sin \ 3\alpha)=` `\frac (cos^3 \alpha-3 sin^2 \alpha cos \alpha)(3 sin \alpha) cos^2 \alpha-sin^3 \alpha)=` `\frac (\frac(cos^3 \alpha-3 sin^2 \alpha cos \alpha)(sin^3 \alpha))(\frac(3 sin \alpha cos^2 \alpha-sin^3 \alpha)(sin^3 \alpha))=` `\frac (\frac( cos^3 \alpha )(sin^3 \alpha)-3 \cdot \ frac(cos \alpha)( sin \alpha ))(3\frac(cos^2 \alpha)(sin^2 \alpha)-1)=` `ctg \ 3\alpha=\frac(ctg^3 \alpha) -3\ctg\\alpha)(3\ctg^2\alpha-1)`.

Pentru a demonstra formulele pentru unghiul ` 4\alpha`, îl puteți reprezenta ca ` 2 \cdot 2\alpha` și încercați formulele unghiului dublu de două ori.

Pentru a obține egalități similare pentru unghiul `5\alpha`, îl puteți scrie ca `3\alpha + 2\alpha` și aplicați identitățile sumei și diferenței unghiurilor și unghiurilor duble și triple.

Toate formulele pentru alte unghiuri multiple sunt derivate în mod similar, dar sunt rareori necesare în practică.

Formulele unghiului dublu sunt folosite pentru a exprima sinusurile, cosinusurile, tangentele, cotangentele unui unghi cu valoarea 2 α, folosind funcțiile trigonometrice ale unghiului α. Acest articol va introduce toate formulele cu unghi dublu cu dovezi. Vor fi luate în considerare exemple de aplicare a formulelor. În partea finală vor fi prezentate formulele pentru unghiurile triple și cvadruple.

Lista formulelor cu unghi dublu

Pentru a converti formulele cu unghi dublu, ar trebui să rețineți că unghiurile din trigonometrie au forma n α notație, unde n este un număr natural, valoarea expresiei este scrisă fără paranteze. Astfel, notația sin n α este considerată a avea același sens ca sin (n α) . Când notăm sin n α, avem o notație similară (sin α) n. Utilizarea notației este aplicabilă tuturor funcțiilor trigonometrice cu puteri n.

Mai jos sunt formulele unghiului dublu:

sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α - sin 2 α , cos 2 α = 1 - 2 · sin 2 α , cos 2 α = 2 · cos 2 α - 1 t g 2 α = 2 t g α 1 - t g 2 α c t g 2 α - c t g 2 α - 1 2 c t g α

Rețineți că aceste formule sin și cos sunt aplicabile cu orice valoare a unghiului α. Formula tangentei cu unghi dublu este valabilă pentru orice valoare a lui α, unde t g 2 α are sens, adică α ≠ π 4 + π 2 · z, z este orice număr întreg. Cotangenta unghiului dublu există pentru orice α, unde c t g 2 α este definită la α ≠ π 2 z.

Cosinusul unui unghi dublu are notația triplă a unui unghi dublu. Toate sunt aplicabile.

Dovada formulelor cu unghi dublu

Dovada formulelor pleacă de la formulele de adunare. Să aplicăm formulele pentru sinusul sumei:

sin (α + β) = sin α · cos β + cos α · sin β și cosinusul sumei cos (α + β) = cos α · cos β - sin α · sin β. Să presupunem că β = α, atunci obținem asta

sin (α + α) = sin α · cos α + cos α · sin α = 2 · sin α · cos α și cos (α + α) = cos α · cos α - sin α · sin α = cos 2 α - sin 2 α

Astfel, sunt dovedite formulele pentru sinusul și cosinusul unghiului dublu sin 2 α = 2 · sin α · cos α și cos 2 α = cos 2 α - sin 2 α.

Formulele rămase cos 2 α = 1 - 2 · sin 2 α și cos 2 α = 2 · cos 2 α - 1 conduc la forma cos 2 α = cos 2 α = cos 2 α - sin 2 α, la înlocuirea lui 1 cu suma pătratelor cu identitatea principală sin 2 α + cos 2 α = 1 . Obținem că sin 2 α + cos 2 α = 1. Deci 1 - 2 sin 2 α = sin 2 α + cos 2 α - 2 sin 2 α = cos 2 α - sin 2 α și 2 cos 2 α - 1 = 2 cos 2 α - (sin 2 α + cos 2 α) = cos 2 α - sin 2 α.

Pentru a demonstra formulele unghiului dublu de tangentă și cotangente, aplicăm egalitățile t g 2 α = sin 2 α cos 2 α și c t g 2 α = cos 2 α sin 2 α. După transformare, obținem că t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α - sin 2 α și c t g 2 α = cos 2 α sin 2 α = cos 2 α - sin 2 α 2 · sin α · cos α . Împărțiți expresia la cos 2 α, unde cos 2 α ≠ 0 cu orice valoare a lui α când este definită t g α. Împărțim o altă expresie cu sin 2 α, unde sin 2 α ≠ 0 cu orice valoare a lui α, când c t g 2 α are sens. Pentru a demonstra formula unghiului dublu pentru tangentă și cotangentă, înlocuim și obținem:

|BD|- lungimea arcului de cerc cu centru într-un punct A.
α - unghi exprimat în radiani.

Sine ( sin α) este o funcție trigonometrică în funcție de unghiul α dintre ipotenuză și catetul unui triunghi dreptunghic, egal cu raportul dintre lungimea catetului opus |BC| la lungimea ipotenuzei |AC|.
cosinus ( cos α) este o funcție trigonometrică în funcție de unghiul α dintre ipotenuză și catetul unui triunghi dreptunghic, egal cu raportul dintre lungimea catetei adiacente |AB| la lungimea ipotenuzei |AC|.

Notatii acceptate

;
;
.

Graficul funcției sinus, y = sin x

Graficul funcției cosinus, y = cos x

Proprietățile sinusului și cosinusului

Periodicitate

Funcțiile y = sin xși y = cos x periodic cu punct 2π.

Paritate

Funcția sinus este impară. Funcția cosinus este pară.

Domeniul definirii si valorilor, extrema, crestere, scadere

Funcțiile sinus și cosinus sunt continue în domeniul lor de definiție, adică pentru tot x (vezi dovada continuității). Principalele lor proprietăți sunt prezentate în tabel (n - întreg).

	y = sin x	y = cos x
Domeniul de aplicare și continuitatea	- ∞ < x < + ∞	- ∞ < x < + ∞
Gama de valori	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Crescând
Descendentă
Maxima, y = 1
Minima, y = - 1
Zerouri, y = 0
Interceptarea punctelor cu axa ordonatelor, x = 0	y = 0	y = 1