Rezumatul lecției "Semnificația fizică și geometrică a derivatei. Tangenta la graficul unei funcții." Lecția „ecuația tangentei la graficul funcției” Scrieți ecuația tangentei
Scopul lecției: Formarea deprinderilor în compilarea unei ecuații a unei tangente la un grafic al unei funcții și luarea în considerare a principalelor tipuri de sarcini USE legate de înțelegerea semnificației geometrice a unei derivate.
Obiectivele lecției:
Tutoriale:
Să sistematizeze abilitățile de aplicare a semnificației geometrice a derivatei.
Pentru a consolida concepte precum „panta tangentei”, „tangenta unghiului de înclinare a tangentei la direcția pozitivă a axei OX”, valoarea derivatei în punctul de contact.
Continuați să dezvoltați abilități în calcularea derivatelor folosind formule și reguli de diferențiere.
să elaboreze și să sistematizeze abilitățile și abilitățile pe tema „Tangenta, ecuația unei tangente la un grafic al funcției”.
În curs de dezvoltare:
promovează dezvoltarea atenției;
dezvoltarea intelectuală, emoțională, personală a elevului;
organizează-te pentru muncă, folosește capacitatea de autoexaminare;
dezvoltarea interesului cognitiv;
promovează dezvoltarea gândirii logice, intuiția matematică;
să promoveze dezvoltarea și înțelegerea legăturilor interdisciplinare între studenți;
Educational:
să cultive perseverența și perseverența în atingerea scopului;
dezvoltarea competențelor comunicative ale elevilor (cultura comunicării, capacitatea de a lucra în grup, capacitatea de a-și argumenta punctul de vedere);
arată frumusețea matematicii;
educația estetică se realizează prin formarea capacității de a întocmi rațional, corect o sarcină într-un caiet, prin mijloace vizuale și didactice.
crearea condițiilor pentru conștientizarea necesității unei acțiuni independente în rezolvarea problemelor;
realizează marea semnificație practică și istorică a derivatului.
Tipul de lecție lectie de consolidare a materialului studiat
Rezultatul planificat al lecției:
1. Elevii cunosc regulile pentru găsirea derivatelor și sunt gata să finalizeze sarcinile USE.
2. Elevii s-au simțit responsabili pentru calitatea și rezultatul muncii desfășurate la lecție.
Forme de muncă de studiu :
individual;
individual - colectiv (în perechi, în grup).
Echipament: tablă interactivă, tablă, foi de lucru cu sarcini din opțiunile de instruire USE și din banca deschisă de sarcini USE, fișă de evaluare, prezentare.
În timpul orelor:
Organizarea timpului
Buna ziua! Mă bucur foarte mult să vă văd pe toți, sper că acest lucru este reciproc și, drept dovadă, vom zâmbi unul altuia și vom începe lecția.
Epigraful lecției sunt cuvintele filozofului materialist francez Denis Diderot (1713 - 1784) - un contemporan al lui Descartes, Leibniz, bibliotecarul personal al Ecaterinei cea Mare. „Puteți începe cercetarea în moduri diferite... Oricum, începutul se dovedește aproape întotdeauna a fi o încercare foarte imperfectă, adesea nereușită. Există adevăruri, precum țările, calea cea mai convenabilă către care devine cunoscută numai după ce am încercat toate căile. Cineva trebuie, riscându-se, să iasă din calea bătută pentru a le arăta altora calea cea bună... Pe drumul către adevăr, suntem aproape întotdeauna sortiți să facem greșeli ”(Denis Diderot) (diapozitiv).
2) Motivarea activității educaționale a elevilor, stabilirea scopurilor și obiectivelor lecției.
În prima jumătate a anului, am explorat o funcție prin graficul acesteia. În acest moment, suntem pe calea studierii funcției după formula ei. Trei pași au fost deja făcuți.
Care sunt acești pași? (Afirmațiile elevilor: am studiat definiția unei derivate, regulile de găsire a derivatelor, ecuația tangentei)
Ce subiect am abordat în lecția anterioară? (Afirmații elevului: ecuația tangentei)
Care sunt obiectivele tale pentru această lecție? (Afirmațiile elevilor: să elaboreze și să sistematizeze abilitățile și abilitățile pe tema „Tangenta, ecuația unei tangente la un grafic de funcție”).
Astăzi vom consolida materialul pe tema „Ecuația tangentei” prin rezolvarea problemelor cheie sau de susținere, vom verifica asimilarea tehnicii de găsire a derivatei și vom explora legătura dintre ecuația tangentei și studiul proprietăților graficului unei funcții , care în viitor ne va oferi un aparat pentru a construi practic un grafic al oricărei funcții și a găsi proprietățile acesteia.
Acordați-vă că astăzi la lecție veți lucra mult pe cont propriu. Accentul lecției va fi „Fișa de punctaj”(Anexa 1). Este în fiecare dintre voi. Introduceți numele și prenumele dvs. După fiecare pas al lecției, evaluează-te și înregistrează rezultatul pe foaia de evaluare. Revedeți criteriile de notare pentru fiecare pas al lecției. La sfârșitul lecției, tu însuți îți vei rezuma munca și vei face o evaluare pentru stăpânirea subiectului.
3. Repetarea cunoștințelor de bază.
3.1. Finalizarea sarcinilor din banca deschisă USE 2 min(UE-1) ( Cererea nr. 2 )
La începutul lecției, vom finaliza sarcina din banca deschisă de sarcini USE pentru mișcare. Cărțile sunt în fața ta.
3.2. Execuția testului.(UE-2)
- Pentru a investiga funcția în viitor, trebuie să puteți găsi derivate ale funcțiilor. Care sunt regulile pentru calcularea instrumentelor derivate? (Răspunde elevul).
Să revizuim utilizarea lor. Hai să o facem Test.(Anexa nr. 3). Codificat ca Isaac Newton numit derivata unei functii. Pentru a face acest lucru, trebuie să găsiți derivatele funcțiilor și să notați în caiet litera corespunzătoare răspunsului corect. (Efectuarea unui test).
Deci, cum a numit Isaac Newton derivata?
Test de autotest. Răspuns: Fluxion (pe diapozitiv).
3.3. Mini proiect.(UE-3)
Lucrarea de creare a unui mini-proiect a trecut prin următoarele etape:
Formularea problemei;
planificarea muncii;
un studiu în care elevul a finalizat sarcinile conform regulii, algoritmului și a făcut o concluzie pe baza rezultatelor lucrării.
prezentarea unui mini-proiect colegilor de clasă, răspunsuri la întrebări despre studiu.
A făcut posibilă organizarea de activități educaționale, menținând un echilibru rezonabil între teorie și practică; integrat cu succes în procesul educațional; asigură nu numai dezvoltarea intelectuală, ci și morală a copiilor, independența, activitatea lor.
- Elevul va spune despre metoda fluxiunilor. (Anexa nr. 4).
Depunerea unui mini-proiect.
Punem rezultatul pe foaia de scor.
3.4. sondaj frontal.(UE-4)
1. Ce se numește secanta pentru graficul funcției y=f(x)?
2. Care dreaptă se numește tangentă la graficul funcției?
3. Care este semnificația geometrică a derivatei?
4. Când este tangenta înclinată la un unghi obtuz față de direcția pozitivă a axei Ox?
5. Când este tangenta înclinată la un unghi ascuțit față de direcția pozitivă a axei Ox?
6. Numiți ecuația tangentei la graficul funcției într-un punct dat în termeni generali.
7. Spuneți algoritmul de compilare a ecuației tangentei la graficul funcției.
Punem rezultatul pe foaia de scor.
4. Rezolvarea problemelor.
4.1. Lucrați în perechi.(UE-5)
- Vi s-au dat cărți pentru a găsi valoarea derivatului la un anumit punct al desenului, pentru a efectua sarcini împreună pe birouri. (Anexa nr. 5). Răspunsurile corecte vor apărea apoi pe ecran. Verificați singur corectitudinea sarcinii. Înregistrați scorul pe foaia de scor.
Finalizarea sarcinilor. Slide Self-Verificare.
4.2. Lucru independent asupra opțiunilor. (UE-6) Sarcinile sunt pregătite pe carduri. (Anexa nr. 5).
Vom efectua lucrări independente individuale asupra opțiunilor de compilare a ecuației tangente. Doi elevi sunt invitați, din fiecare opțiune, să lucreze pe un avion cu tablă închis de clasă. Pentru cei care fac față muncii independente mai repede decât soluția finită apare pe tablă, îndeplinește o sarcină suplimentară.
Pe măsură ce lucrarea progresează, profesorul verifică munca elevilor la tablă. Restul verifică corectitudinea deciziilor lor cu privire la soluțiile de pe tablă, deoarece acestea au fost deja verificate de profesor.
Autotestare.
Punem rezultatul pe foaia de scor.
4.3. Lucru de grup. (UE-7) Se formează grupe, ținând cont de abilitățile matematice ale copiilor, fiecărei grupe i se oferă cartonașe cu diferite tipuri de sarcini. Patru oameni lucrează cu cardul. În grup există o rezolvare comună a sarcinii și un elev din grup raportează despre munca depusă. Verificarea îndeplinirii sarcinilor de către profesor.
Lucrăm în echipe permanente. Îndeplinesc sarcina de a aplica semnificația geometrică a derivatei. Hotărâm împreună și un elev din grup va raporta despre munca depusă.
Finalizarea sarcinilor.
Verificăm. Punem rezultatul pe foaia de scor.
5. Temă: Itemul 19 (ecuația tangentă, sensul geometric al derivatei), p. 134 Nr. 256 (c, d), Nr. 257 (a, b), p. 171 Nr. 4 (3 (a)). Sarcină practică de pe card:
6. Reflecție. Rezumatul lecției.
Vă rugăm să calculați totalul de puncte pentru lecția de astăzi și să vă puneți o notă în conformitate cu criteriile din fișa de evaluare, subliniați în opinia dumneavoastră afirmațiile corecte din tabelul „Rezultatele lecției”
Mulțumesc pentru lecție, a fost o plăcere să lucrez cu tine. La revedere!
Bibliografie:
1.Manual-Algebra și începutul analizei: Proc. Pentru 10-11 celule. educatie generala instituții / A.N. Kolmogorov, A.M. Abramov, Yu.P. Dudnitsyn și alții; Ed. A.N. Kolmogorova - M ..: Educație, 2011
2. Wozniak G.M. Relația dintre teorie și practică în procesul studierii matematicii. - K .: Şcoala Radianska, 1989.
3. Dicționar enciclopedic al unui tânăr matematician / Comp. Savin A.P. - M.: Pedagogie, 1985.
Ediții electronice:
Marea Enciclopedie Rusă. - „Chiril și Metodiu”, 2002.
Cererea nr. 1
Lecție pe tema „Ecuația tangentei”
Scopul lecției:
Dezvoltați abilitățile și abilitățile în compilarea ecuației tangente pentru diverse funcții și aplicarea semnificației geometrice a derivatei.
| Număr educational element | Material didactic care indică sarcinile | Sfaturi pentru profesori | Notă |
| UE-1 | Finalizarea misiunilor de la o bancă USE deschisă Ţintă : Pregătirea pentru examen Perioada de graţie: 3 minute. | Criterii de evaluare: 4 răspunsuri corecte - „5” 3 răspunsuri corecte - „4” 2 răspunsuri corecte - „3” | Nota:______ |
| UE-2 | Execuția testului. Ţintă : testarea cunoștințelor regulilor de bază de diferențiere. Perioada de graţie: 5 minute. Test de autotest. | Criterii de evaluare: 7 răspunsuri corecte - „5” 6.5 răspunsuri corecte - „4” 4.3 răspunsuri corecte - „3” | Nota:______ |
| UE-3 | Referință istorică. Ţintă : extinderea orizontului. | Memorează termeni noi. | Subliniază-ți atitudinea față de ceea ce ai auzit: memorat A luat notă Interesat. |
| UE-4 | Verificarea informațiilor teoretice de bază. | subliniază stiu ferm Pot să răspund cu un indiciu Nu știu prea multe |
|
| UE-5 | Lucrați în perechi țintă: Să dezvolte abilitățile și abilitățile de aplicare a semnificației geometrice a derivatei Perioada de graţie: 3 minute. | Criterii de evaluare: A finalizat 2 sarcini. dreapta - "5" A terminat corect 1 fund și a început să-l execute pe al 2-lea corect - "4" A finalizat 1 sarcină. - "3" | Nota:______ |
| UE-6 | Muncă independentă. Scrieți soluția în caiet Perioada de graţie: Perioada de graţie: 5 minute. | subliniază A rezolvat corect sarcina a rezolvat incorect problema |
|
| UE-7 | Lucru de grup Scrieți soluția în caiet Perioada de graţie: 5 minute. | subliniază rezolvat sarcina a rezolvat incorect problema. |
Rezumatul lecției:
Cred că astăzi la lecție am lucrat pentru ______(evaluare)
Cererea nr. 2
Opțiunea 1
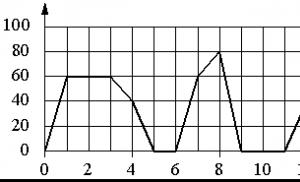
1. Graficul arată dependența de timp a vitezei unui autobuz obișnuit. Axa verticală arată viteza autobuzului în km/h, axa orizontală arată timpul în minute de la pornirea autobuzului.
 program, potriviți fiecare interval de timp cu caracteristicile deplasării autobuzului la acest interval.
program, potriviți fiecare interval de timp cu caracteristicile deplasării autobuzului la acest interval.
| INTERVALE DE TIMP | CARACTERISTICI |
| A) 4-8 min. | 1) a avut loc o oprire de 2 minute |
| B) 8--12 minute | 2) viteza nu mai mică de 20 km/h pe tot intervalul |
| C) 12-16 min. | 3) viteza nu este mai mare de 60 km/h |
| D) 18-22 min. | 4) a avut loc o oprire care a durat exact 1 minut |
În tabelul de lângă fiecare literă indicați numărul corespunzător.
Opțiunea 2
Graficul arată dependența vitezei unei mașini de timp. Pe axa verticală este viteza mașinii în km/h, pe orizontală - timpul în secunde scurs de la pornirea mașinii

Folosind graficul, potriviți fiecare interval de timp cu caracteristicile mișcării mașinii în acest interval.
| INTERVALE DE TIMP | CARACTERISTICI |
| A) 0-30s | 1) viteza mașinii a atins maximul pentru tot timpul în care mașina a fost în mișcare |
| B) 30-60 s | 2) viteza mașinii nu a scăzut și nu a depășit 40 km/h |
| C) 60-90 s | 3) mașina s-a oprit timp de 15 secunde |
| D) 90-120 s | 4) viteza mașinii nu a crescut pe tot parcursul intervalului |
În tabelul de lângă fiecare literă indicați numărul corespunzător
Cererea nr. 3
Test
Aflați derivata funcției:
y=x2+3sinx 2) y= 3) y= 4) y=cos3x 5)y= 6)y=cos(4x-1) 7)y=sin2x
C- y’= F- y’=2x+3cosx I- y’=sin2x L- y’=3x5 I- y’=-4 sin(4x-1)
Yu-y’= K-y’=-3 sin3х
Cererea nr. 4
Istoria apariției derivatului.
Conceptul de derivată a apărut în legătură cu necesitatea de a rezolva o serie de probleme din fizică, mecanică și matematică. Onoarea de a descoperi legile de bază ale analizei matematice aparține omului de știință englez Newton și matematicianului german Leibniz.
Poetul englez Alexander Pope a descris timpul după cum urmează:
Această lume era învăluită în întuneric adânc.
Să fie lumină! Și iată că vine Newton.
Celebrul fizician Isaac Newton, care s-a născut în satul englez Woolstrop, a adus o contribuție semnificativă la matematică. Rezolvând probleme la desenarea tangentelor la curbe, calculând ariile figurilor curbilinii, el a creat o metodă generală de rezolvare a unor astfel de probleme - metoda fluxurilor (derivate) și a numit derivata în sine fluentă. El a calculat derivata și integrala funcției de putere. Despre calculul diferențial și integral scrie în lucrarea sa „Metoda fluxurilor” (1665 - 1666), care a servit drept unul dintre începuturile analizei matematice, calculului diferențial și integral. Metoda fluxiunii se aplică aici unui număr mare de întrebări geometrice (sarcini privind tangente, curbură, extreme, cuadraturi, redresări etc.).
Această descoperire a lui Newton a fost un punct de cotitură în istoria științelor naturale.
Onoarea de a descoperi legile de bază ale analizei matematice, alături de Newton, îi aparține matematicianului german Gottfried Wilhelm Leibniz.
Leibniz a ajuns la aceste legi rezolvând problema trasării unei tangente la o curbă arbitrară, adică. a formulat sensul geometric al derivatei, că valoarea derivatei în punctul de contact este panta tangentei sau tg panta tangentei cu direcția pozitivă a axei OX.
Mulți oameni de știință din diferiți ani au fost interesați de tangentă. Ocazional, conceptul de tangente a fost întâlnit în lucrările matematicianului italian N. Tartaglia (c. 1500 - 1557) - aici a apărut tangenta în cursul studierii problemei unghiului de înclinare a pistolului, care asigură cea mai mare date a zborului proiectilului. I. Keppler a considerat tangenta în cursul rezolvării problemei celui mai mare volum al unui paralelipiped înscris într-o bilă de rază dată.
În secolul al XVII-lea, pe baza teoriei mișcării lui G. Galileo, a fost dezvoltat activ conceptul cinematic al derivatului. Diverse opțiuni de prezentare se găsesc în R. Descartes.
Termenul derivat și denumirile moderne y’ , f ’ au fost introduse de J. Lagrange în 1797.
Cererea nr. 5 
Cererea nr. 6 
Opțiunea 1
Opțiunea 2
Compuneți ecuația tangentei la graficul funcției în punctul cu abscisa
Sarcină suplimentară: Echivalează tangenta la grafic
funcțiile y=f(x) în punctul cu abscisă x0. x0=2
Cererea nr. 7
Linia y = 6x +9 este tangentă la graficul funcției
y \u003d x3 -4x2 + 9x + 14. Găsiți abscisa punctului de contact.
Linia y = 6x + 8 este paralelă cu tangenta la graficul funcției
y \u003d x² + 7x - 6. Aflați abscisa punctului de contact
La ce valoare a lui a este linia y \u003d 3x + o tangentă la graficul funcției y \u003d 2x² - 5x + 1?
Tip de lecție:învăţarea de materiale noi.
Metode de predare: vizuală, parțial exploratorie.
Scopul lecției:
- Introduceți conceptul de tangentă la graficul unei funcții într-un punct, aflați care este semnificația geometrică a derivatei, deduceți ecuația tangentei și învățați cum să o găsiți pentru anumite funcții.
- Dezvoltarea gândirii logice, a abilităților de cercetare, a gândirii funcționale, a vorbirii matematice.
- Dezvoltarea abilităților de comunicare în muncă, pentru a promova dezvoltarea activității independente a elevilor.
Echipament: computer, proiector multimedia, fișe.
Descarca:
Previzualizare:
Lecție pe tema „Tangentă. Ecuația tangentei”
Tip de lecție: învăţarea de materiale noi.
Metode de predare:vizuală, parțial exploratorie.
Scopul lecției:
- Introduceți conceptul de tangentă la graficul unei funcții într-un punct, aflați care este semnificația geometrică a derivatei, deduceți ecuația tangentei și învățați cum să o găsiți pentru anumite funcții.
- Dezvoltarea gândirii logice, a abilităților de cercetare, a gândirii funcționale, a vorbirii matematice.
- Dezvoltarea abilităților de comunicare în muncă, pentru a promova dezvoltarea activității independente a elevilor.
Echipament: computer, proiector multimedia, fișe.
Planul lecției
I moment organizatoric.
Verificarea gradului de pregătire a elevilor pentru lecție. Mesajul temei și motto-ul lecției.
II Actualizarea materialului.
(Activați atenția, arătați lipsa de cunoștințe despre tangentă, formulați scopurile și obiectivele lecției.)
Să discutăm ce este o tangentă la un grafic al funcției? Sunteți de acord cu afirmația că „O tangentă este o dreaptă care are un punct comun cu o curbă dată”?
Există o discuție. Declarații ale copiilor (da și de ce, nu și de ce). În timpul discuției, ajungem la concluzia că această afirmație nu este adevărată.
Exemple.
1) Linia x = 1 are un punct comun M(1; 1) cu parabola y = x2, dar nu este tangentă la parabola. Linia y = 2x – 1 care trece prin același punct este tangentă la parabola dată.
2) În mod similar, linia x = π nu este tangentă la grafic y = cos x , deși are singurul punct comun K(π; 1) cu el. Pe de altă parte, dreapta y = - 1 care trece prin același punct este tangentă la grafic, deși are infinite de puncte comune ale formei cu acesta;(π+2 πk; 1), unde k este un număr întreg, în fiecare dintre ele atinge graficul.
|
|
Stabilirea scopurilor și obiectivelor pentru copii la lecție:aflați care este tangenta la graficul unei funcții într-un punct, cum să scrieți o ecuație pentru o tangentă?
De ce avem nevoie pentru asta?
Amintiți-vă forma generală a ecuației unei drepte, condițiile pentru linii paralele, definiția unei derivate, regulile de diferențiere.
III Lucrări pregătitoare pentru studiul materialului nou.
Material de întrebări pe cartonașe: (sarcinile sunt finalizate pe tablă)
1 elev: completați tabelul de derivate ale funcțiilor elementare 
2 elev: amintiți-vă regulile de diferențiere 
3 elev: scrieți ecuația unei drepte y = kx + 4 trecând prin punctul A(3; -2).
(y=-2x+4)
4 elev: alcătuiește o ecuație de drepte y=3x+b trecând prin punctul С(4; 2).
(y = 3x - 2).
Cu restul lucru frontal.
- Formulați definiția unei derivate.
- Care dintre următoarele drepte sunt paralele? y = 0,5x; y \u003d - 0,5x; y \u003d - 0,5x + 2. De ce?
Ghiciți numele omului de știință: 
Cheia răspunsurilor
Cine a fost acest om de știință, cu ce este legată munca lui, vom afla în lecția următoare.
Verificați răspunsurile elevilor pe carduri.
IV Studiul materialului nou.
Pentru a stabili ecuația unei drepte pe un plan, este suficient să cunoaștem unghiul acesteia
coeficientul și coordonatele unui punct.
- Să începem cu panta

Figura 3
Luați în considerare graficul funcției y = f(x) diferentiabil la punctul A(x 0 , f(x 0 )) .
Alegeți un punct pe el M (x 0 + Δх, f(x 0 + Δх)) si trage o secanta A.M .
Întrebare: care este panta secantei? (∆f/∆x=tgβ)
Vom aproxima punctul de-a lungul arcului M până la punctul A . În acest caz, drept A.M se va roti în jurul punctului A , apropiindu-se (pentru linii netede) de o poziție limitativă - o linie dreaptă LA . Cu alte cuvinte, AT , care are această proprietate, se numește tangentă la graficul funcției y \u003d f (x) în punctul A (x 0, f (x 0)).
Panta secantei AM la AM → 0 tinde spre panta tangentei AT Δf/Δx → f "(x 0 ) . Valoarea derivatei într-un punct x 0 luați pentru panta tangentei. Ei spun astatangenta este poziția limită a secantei la ∆х → 0.
Existența unei derivate a unei funcții într-un punct x 0 este echivalentă cu existența unei tangente (neverticale) la (x 0, f(x 0 )), în timp ce panta tangentei este egală cu f "(x 0) . Aceasta este sensul geometric al derivatului.
Definiția tangentei: Tangenta la un grafic diferentiabil intr-un punct x 0 funcția f este o dreaptă care trece printr-un punct(x 0 , f(x 0 )) și având o pantă f "(x 0) .
Să desenăm funcțiile tangente la grafic y \u003d f (x) în punctele x 1, x 2, x 3 , și notați unghiurile pe care le formează cu axa x. (Acesta este unghiul măsurat în direcția pozitivă de la direcția pozitivă a axei la linia dreaptă.)

Figura 4
Vedem că unghiul α 1 este acut, unghiul α 3 este obtuz și unghiul α 2 este zero deoarece linia l este paralel cu axa Ox. Tangenta unui unghi ascuțit este pozitivă, un unghi obtuz este negativ. De aceea f "(x 1)> 0, f" (x 2) \u003d 0, f "(x 3)
- Acum derivăm ecuația tangenteila graficul funcției f în punctul A(x 0 , f(x 0 ) ).
Vedere generală a ecuației dreptei y = kx + b .
- Să găsim coeficientul unghiular k \u003d f "(x 0), obținem y \u003d f "(x0) ∙ x + b, f (x) \u003d f "(x 0 )∙x + b
- Să găsim b. b \u003d f (x 0) - f "(x 0) ∙ x 0.
- Înlocuiți valorile obținute k și b în ecuația unei linii drepte: y \u003d f "(x 0) ∙x + f (x 0) - f "(x 0) ∙x 0 sau y \u003d f (x 0) + f "(x 0) (x - x 0)
- Generalizarea materialului de curs.
- formulați un algoritm pentru găsirea ecuației tangentei la un punct?
1. Valoarea funcției la punctul de contact
2. Derivată comună a unei funcții
3. Valoarea derivatei la punctul de contact
4. Înlocuiți valorile găsite în ecuația generală a tangentei.
V Consolidarea materialului studiat.
1. Lucrare orală:
1) B ce puncte ale graficului sunt tangente la acesta
a) orizontală;
b) formează un unghi ascuțit cu axa x;
c) formează un unghi obtuz cu axa x?
2) Pentru ce valori ale argumentului este derivata funcției date de grafic
a) egal cu 0;
b) mai mult de 0;
c) mai mic de 0?
|
|
3) Figura prezintă graficul funcției f(x) și o tangentă la acesta într-un punct cu o abscisă x0 . Aflați valoarea derivatei unei funcții f „(x) în punctul x 0 .

Figura 7
2. Lucrări scrise.
Nr. 253 (a, b), Nr. 254 (a, b). (lucru de teren, cu comentarii)
3. Rezolvarea problemelor de referință.
Să luăm în considerare patru tipuri de sarcini. Copiii citesc starea problemei, oferă un algoritm de soluție, unul dintre elevi îl întocmește pe tablă, restul îl notează într-un caiet.
1. Dacă este dat un punct de atingere
Scrieți o ecuație pentru o tangentă la un grafic al funcției f(x) = x 3 - 3x - 1 în punctul M cu abscisă -2.
Soluţie:
- Să calculăm valoarea funcției: f(-2) =(-2) 3 - 3(-2) - 1 = -3;
- găsiți derivata funcției: f "(x) \u003d 3x 2 - 3;
- calculați valoarea derivatei: f "(-2) \u003d - 9 .;
- să substituim aceste valori în ecuația tangentei: y = 9(x + 2) - 3 = 9x + 15.
Răspuns: y = 9x + 15.
2. După ordonata punctului de contact.
Scrieți o ecuație pentru o tangentă într-un punct dintr-un grafic cu ordonata y 0 = 1.
Soluţie:
Răspuns: y \u003d -x + 2.
3. Direcția prestabilită.
Scrieți ecuații tangente la grafic y \u003d x 3 - 2x + 7 , paralel cu linia y = x .
Soluţie.
Tangenta dorită este paralelă cu dreapta y=x . Deci au aceeași pantă k \u003d 1, y "(x) \u003d 3x2 - 2. Abscisa x 0 punctele de contact satisface ecuația 3x 2 - 2 \u003d 1, de unde x 0 = ±1.
Acum putem scrie ecuațiile tangente: y = x + 5 și y = x + 9 .
Răspuns: y = x + 5 , y = x + 9 .
4. Condiții pentru atingerea graficului și a dreptei.
Sarcină. La ce b drept y = 0,5x + b este tangentă la graficul funcției f(x) = ?
Soluţie.
Reamintim că panta unei tangente este valoarea derivatei în punctul tangentei. Panta acestei drepte este k = 0,5. De aici obținem ecuația pentru determinarea abscisei x a punctului de atingere: f "(x) \u003d = 0,5. Evident, singura sa rădăcină este x = 1. Valoarea acestei funcții în acest punct este y(1) = 1. Deci, coordonatele punctului de atingere sunt (1; 1). Acum rămâne să alegeți o valoare a parametrului b pentru care linia trece prin acest punct, adică coordonatele punctului satisfac ecuația dreptei: 1 = 0,5 1 + b, de unde b = 0,5.
5. Munca independentă cu caracter didactic.
Lucrați în perechi. 
Verificare: rezultatele soluției se trec într-un tabel pe tablă (un răspuns din fiecare pereche), discutarea răspunsurilor.
6. Aflarea unghiului de intersecție a graficului unei funcții și a unei drepte.
Unghiul de intersecție a graficului funcției y = f(x) și linia directă l numit unghiul la care tangenta la graficul functiei intersecteaza dreapta in acelasi punct.
Nr. 259 (a, b), Nr. 260 (a) - dezasamblați la bord.
7. Munca independenta de natura controlanta.(lucrare diferențiată, profesorul verifică pentru următoarea lecție)
1 opțiune.
Opțiunea 2.
- În ce puncte este tangenta la graficul funcției f(x) = 3x 2 - 12x + 7 paralel cu axa x?
- Echivalează tangenta cu graficul funcției f(x)= x 2 - 4 în punctul cu abscisa x 0 = - 2. Desenați modelul.
- Aflați dacă linia este y \u003d 12x - 10 tangentă la graficul funcției y = 4x3.
3 optiune.
VI Rezumând lecția.
1. Răspunsuri la întrebări
- ce se numește tangentă la graficul unei funcții într-un punct?
Care este semnificația geometrică a derivatei?
- formulați un algoritm pentru găsirea ecuației tangentei la un punct?
2. Amintiți-vă de scopurile și obiectivele lecției, am atins acest scop?
3. Care au fost dificultățile din lecție, ce momente ale lecției ți-au plăcut cel mai mult?
4. Notarea pentru lecție.
VII Comentariu la teme: p. 19 (1, 2), Nr. 253 (c), Nr. 255 (d), Nr. 256 (d), Nr. 257 (d), Nr. 259 (d). Pregătește un raport despre Leibniz.
Literatură
1. Algebra și începuturile analizei: un manual pentru clasa a 10-a a instituțiilor de învățământ. Compilatoare:. M. Nikolsky, M. K. Potapov, N. N. Reshetnikov, A. V. Shevkin. - M.: Educație, 2008.
2. Materiale didactice despre algebră și principii de analiză pentru clasa a 10-a / B.M. Ivlev, S.M. Saakyan, S.I. Schwarzburd. - M.: Educație, 2008.
3. Disc multimedia al companiei „1C”. 1C: Tutor. Matematică (partea 1) + opțiuni USE. 2006.
4. Banca deschisă de sarcini în matematică/ http://mathege.ru/
slide 2
Definitia este corecta?
O tangentă este o dreaptă care are un punct comun cu o curbă dată.
slide 3
Să fie date două drepte și având un punct comun M (1; 1) cu parabola dată.
slide 4
În această lecție:
aflați ce este o tangentă la graficul unei funcții într-un punct, cum să scrieți o ecuație pentru o tangentă; luați în considerare principalele sarcini pentru compilarea ecuației tangente. Pentru a face acest lucru: amintiți-vă forma generală a ecuației dreptei, condiția dreptelor paralele, definiția derivatei regulii de diferențiere Formule de diferențiere
slide 5
Definiție derivată
Să fie definită funcția într-un interval care conține un punct în interior. Să dăm argumentului un increment astfel încât să nu iasă din acest interval. Să găsim incrementul corespunzător al funcției și să alcătuim raportul.Dacă există o limită a raportului la, atunci limita specificată se numește derivată a funcției într-un punct și se notează.
slide 6
Reguli de diferențiere
Derivata sumei este egala cu suma derivatelor. Factorul constant poate fi scos din semnul derivatei. Derivata produsului a doua functii este egala cu suma a doi termeni; primul termen este produsul derivatei primei funcții și a celei de-a doua funcție, iar al doilea termen este produsul primei funcție și derivatei celei de-a doua funcție. derivată a coeficientului
Slide 7
Formule de diferențiere de bază
Slide 8
Două drepte sunt paralele dacă și numai dacă panta lor este egală
Sunt liniile paralele?
Slide 9
Să fie dat graficul funcției y=f(x). Pe el se alege un punct M(a;f(a)), în acest punct se trasează o tangentă la graficul funcției (presupunem că există). Aflați panta tangentei.
Slide 10
Sensul geometric al derivatului
Dacă o tangentă care nu este paralelă cu axa y poate fi desenată pe graficul funcției y \u003d f (x) într-un punct, atunci exprimă panta tangentei
slide 11
Derivata într-un punct este egală cu panta tangentei la graficul funcției y = f(x) în acel punct. Acestea. Mai mult, dacă: .
slide 12
Derivarea ecuației tangentei
Fie linia dreaptă dată de ecuația: ecuația tangentei la graficul funcției
slide 13
Scrieți o ecuație pentru o tangentă:
la graficul unei funcții într-un punct
Slide 14
la graficul unei funcții într-un punct
slide 15
Algoritm pentru găsirea ecuației tangentei la graficul funcției y=f(x).
Să notăm abscisa punctului de contact cu litera x=a. Să calculăm. Să găsim și Înlocuiți numerele găsite a în formulă
slide 16
Scrieți o ecuație pentru tangenta la graficul unei funcții într-un punct.
Slide 17
Desenați o tangentă la graficul funcției astfel încât să fie paralelă cu dreapta.
Slide 18
Slide 19
Muncă independentă
Slide 20
Numerele din manual
Nr. 29.3 (a, c) Nr. 29.12 (b, d) Nr. 29.18 Nr. 29.23 (a)
diapozitivul 21
Răspunde la întrebările:
Ce se numește tangentă la graficul unei funcții într-un punct? Care este semnificația geometrică a derivatei? Formulați un algoritm pentru găsirea ecuației tangentei?
slide 22
Teme pentru acasă
Nr. 29.3 (b, d) Nr. 29.12 (a, c) Nr. 29.19 Nr. 29.23 (b)
slide 23
Literatură
Algebra și începutul analizei matematice: Proc. Pentru 10-11 celule. pentru studenții instituțiilor de învățământ (nivel de bază) / Editat de A.G. Mordkovici. - M.: Mnemosyne, 2009. Algebra și începutul analizei matematice: Cartea problemelor, Pentru 10-11 celule. pentru studenții instituțiilor de învățământ (nivel de bază) / Editat de A.G. Mordkovici. - M.: Mnemosyne, 2009. Algebra și începuturile analizei. Muncă independentă și de control pentru clasele 10-11. / Ershova A.P., Goloborodko V.V. – M.: ILEKSA, 2010 USE 2010. Matematică. Sarcina B8. Caiet de lucru / Editat de A.L. Semenov și I.V. Yashchenko - M .: Editura MTsNMO, 2010
Vizualizați toate diapozitivele
Planul lecției în clasa a 10-a
„Ecuația tangentei la graficul funcției”
Tip de lecție: Lecția de prezentare primară a noilor cunoștințe și formarea deprinderilor inițiale de subiect, stăpânirea deprinderilor de subiect.
Sarcina didactică a lecției: Asigurarea conștientizării și asimilarii conceptelor, regulilor, algoritmilor; formarea deprinderilor de aplicare a prevederilor teoretice în condiţiile rezolvării problemelor educaţionale.
Obiectivele lecției: retrage ecuația unei tangente la un grafic al unei funcții, pentru a învăța cum să scrieți o ecuație a unei tangente pentru o funcție dată la un punct dat.
Rezultate planificate:
ZUN-uri. Elevii ar trebui
cunoașteți: ecuația tangentei la graficul funcției în punctul x 0 ;
să poată: să întocmească o ecuaţie a unei tangente la graficul unei funcţii date într-un punct dat.
formarea deprinderii de a întocmi o ecuație a unei tangente la un grafic al unei funcții date într-un punct dat.
Echipament: tablă, calculator, proiector, ecran, manuale, caiete studenți, papetărie.
Profesor: Nesterova Svetlana Yurievna
Buna baieti! Toată lumea este pregătită pentru lecție? Te poți așeza.1 tobogan. „Tangentă la graficul unei funcții”
Lucrare orală care vizează pregătirea elevilor pentru perceperea unui subiect nou (repetarea materialului studiat anterior)
10.01 – 10.03
Frontal
munca orală
Pentru a trata calitativ subiectul lecției de astăzi, trebuie să ne amintim ceea ce am studiat anterior.
Răspunde la următoarele întrebări.
2 tobogan.
Care grafic al funcției este o linie dreaptă?(liniar)
Ce ecuație definește o funcție liniară?(y = k x + b )
Care este numele numărului de dinainteX »? ( coeficient de panta direct)
O altă ecuațiey= k x + b se numește ecuația unei drepte cu pantă.
3 slide.
Care este panta dreptei?(tangenta unghiului de inclinare al dreptei, pe care aceasta dreapta o formeaza cu directia pozitiva a axei Ox).
Formulați definiția unei tangente:(linia care trece prin punctul (x O ; f (X O )), cu segmentul căruia graficul se îmbină practic diferentiabil la x O funcții f pentru valorile x apropiate de x O ).
4 slide.
Dacă în punctul x o există derivat , Acea există tangentă (non-vertical) la graficul funcției în punct X o .
5 slide.
Dacă f ’ ( X 0 ) nu există, atunci nici tangenta
nu există (cum ar fi funcția y = |x|),
sau verticală (ca în graficul y \u003d 3 √x).
6 diapozitiv.
Amintiți-vă, care poate fi poziția relativă a tangentei cu axa x?
Creștere directă => pantăk >0, tg> 0 => unghi ascuțit.
Linie dreaptă // Axa OX => pantăk=0, tg= 0 => unghi = 0 0
Coborâre directă => pantăk <0, tg < 0 =>unghi obtuz.
7 slide.
Semnificația geometrică a derivatei:
Panta tangentei este egală cu valoarea derivatei funcției în punctul în care este trasată tangentei k = f `( X o ).
Bine, bine făcut, repetiția s-a terminat.
Subiectul lecției. Stabilirea scopului lecției
10.03-10.05
Discuție, conversație
Finalizați următoarea sarcină:
Dată o funcție y = x 3 . Scrie ecuația tangentei la graficul acestei funcții în punctul x 0 = 1.
PROBLEMĂ? Da. Cum să o rezolv? Care sunt opțiunile tale? Unde puteți găsi ajutor cu această problemă? Ce surse? Dar este problema rezolvabilă? Deci, care crezi că va fi subiectul lecției noastre?
Tema lecției de astăzi"Ecuația tangențială" .
Ei bine, acum formulează obiectivele lecției noastre (COPII):
1. Deduceți ecuațiile tangentei la graficul funcției din punctX O .
2. Aflați cum să scrieți o ecuație tangentă pentru o funcție dată.
Deschidem caiete, notăm numărul, „lucrarea clasei”, tema lecției în margine.
Percepția primară și asimilarea noului material educațional teoretic
10.06- 10.12
Frontal
Căutare - cercetare
8 slide.
Să rezolvăm această problemă practică. Scriu pe tablă - tu privești, raționezi cu mine.
Dată o funcție y = x 3 . Este necesar să scrieți ecuația tangentei la graficul acestei funcții în punctul x 0 = 1.
Argumentăm: ecuația unei drepte cu pantă are forma:y= k x + b .
Pentru a o scrie, trebuie să cunoaștem valoareak Și b .
Sa gasim k (din sensul geometric al derivatului):
k = f `( X o ) = f `(1) = 3 * 1 2 = 3, adică k = 3 .
Ecuația noastră devine:= 3x + b .
Amintiți-vă: dacă o linie dreaptă trece printr-un punct dat, atunci când înlocuiți coordonatele acestui punct în ecuația unei drepte, ar trebui să se obțină egalitatea corectă. Deci, trebuie să găsim ordonata punctului - valoarea funcției în punctul x 0 = 1: f (1) =1 3 =1. Punctul de atingere are coordonate (1; 1).
Înlocuim valorile găsite în ecuația unei linii drepte, obținem:
1 = 3 . 1+ b ; Mijloace b=-2 .
Înlocuiți valorile găsitek = 3 Și b=-2 în ecuația unei linii drepte:y = 3x - 2.
Problema rezolvata.
9 slide.
Și acum vom rezolva aceeași problemă într-o formă generală.
Dată o funcție y= f ( X ), este necesar să scriem ecuația tangentei la graficul acestei funcții în punctul x 0 .
Argumentăm după aceeași schemă: ecuația unei drepte cu pantă are forma:y= k x + b .
Din sensul geometric al derivatului: k = f `( X o )=> y= f `( X o ) * x + b .
Valoarea funcției în punctul x 0 da f ( X o ), deci tangenta trece prin punctul cu coordonate( X 0 ; f ( X o ))=> f ( X o )= f `( X o ) * X o + b .
Exprimă din această înregistrare b : b = f ( X o ) - f `( X o ) * X o .
Înlocuiți toate expresiile din ecuația unei linii drepte:
y= f `( X o ) * x + b = f `( X o ) * x + f ( X o ) - f `( X o ) * X o = f `( X o ) * ( X - X o )+ f ( X o ).
COMPARAȚI CU MANUAL (pagina 131)
Vă rugăm să găsiți intrarea ecuației tangentei în textul manualului și să comparați cu ceea ce am obținut.
Intrarea este puțin diferită (prin ce?), dar este corectă.
Se obișnuiește să scrieți ecuația tangentei în următoarea formă:
y= f ( X o ) + f `( X o )( X - X o )
Scrie această formulă în caiet și evidențiază - trebuie să o știi!
9 slide.
Și acum să facem un algoritm pentru găsirea ecuației tangente. Toate „sfaturile” sunt în formulă.
Găsiți valoarea unei funcții într-un punctX O
Calculați derivata unei funcții
Aflați valoarea derivatei unei funcții într-un punctX O
Înlocuiți numerele rezultate în formulă
y = f ( X o ) + f `( X o )( X – X o )
Aduceți ecuația la forma standard
Dezvoltarea competențelor primare
10.12-10.14
Frontal
Discuție scrisă + comună
Cum funcționează această formulă? Să ne uităm la un exemplu. Scriem un exemplu într-un caiet.
Scrieți ecuația tangentei la graficul funcției f (X) \u003d x 3 - 2x 2 + 1 în punctul cu abscisa 2.
Efectuăm derivarea ecuației cu o înregistrare pe tablă și în caiete.
Răspuns: y \u003d 4x - 7.
Lucrul cu sursa de informații
10.14-10.15
Individual
Citirea textului, discuție
Uită-te în manualul de la p. 131, exemplu 2. Citiți până la punctul 3. Despre ce este vorba în acest exemplu? (puteți face o ecuație pentru o funcție dată într-o formă generală și apoi găsiți ecuația tangentei pentru orice valoare a lui x 0 , și puteți găsi, de asemenea, punctul de intersecție al tangentei la parabola standard cu axa Ox
Pauza dinamica
10.15-10.16
Odihnă
Un moment de odihnă.
Slide - exerciții pentru corp, exerciții pentru ochi.
Aplicarea prevederilor teoretice in conditiile realizarii exercitiilor si rezolvarii problemelor
10.16- 10.30
Frontal, individual
Scris (tabliță + caiet)
Ei bine, acum să trecem la lucrări practice, al căror scop este de a forma abilitățile de a compila ecuația tangentei.
Pe tablă scrieți nr. 255 (a, b), 256 (a, b),rezerva 257 (a, b),* .
* - sarcina de la următorul nivel de complexitate pentru cei mai pregătiți elevi: Pe o parabolă y \u003d 3x 2 - 4x + 6 găsiți punctul în care linia tangentă la ea // y \u003d 2x + 4 și scrieți ecuația tangentei la parabolă în acest punct.
Elevii sunt invitați să lucreze la consiliu (la rândul lor).
Raspunsuri:
№255
a) y \u003d - 3x - 6, y \u003d - 3x + 6 b) y \u003d 2x, y \u003d - 2x +4
№256
a) y \u003d 3, y \u003d - 3x + 3π b) y \u003d 2x + 1 - π / 2, y \u003d 4x + √3 - 4 π / 3
№257 (rezervă)
a) x \u003d 1, y \u003d 1, în t. (1; 1) tangentă // Ox
b) x \u003d - 2, y \u003d - 24, în t. (-2; -24) tangentă // Oh
Sarcina *raspuns:
A (1; 5), ecuația tangentei y \u003d 2x + 3.
Utilizarea independentă a abilităților
10.30-10.35
Grup, individual, independent
Scris (caiet), discuție de lucru în perechi
Deci ce făceam? Cine înțelege materialul? Cine are întrebări? Vom conduce un autocontrol al înțelegerii subiectului lecției.
Veți lucra în perechi - pe mese aveți cărți cu sarcini. Citiți cu atenție sarcina, sunt acordate 4-5 minute pentru a finaliza lucrarea.
Sarcină: Scrieți o ecuație pentru o tangentă la o funcție datăf(X) într-un punct cu o abscisă dată.
eu: f( X) = x 2 - 2x - 8, în punctul cu abscisa -1. Răspuns: y \u003d -4x - 9.
II: f( X) = 2x 2 - 4x + 12, în punctul cu abscisa 2. Răspuns: y = 4x + 4.
III: f( X) = 3x 2 - x - 9, în punctul cu abscisa 1. Răspuns: y \u003d 5x -12.
IV: f( X) = 4x 2 + 2x + 3, în punctul cu abscisa -0,5. Răspuns: y = -2x + 2.
Verificarea efectuării muncii independente
10.35-10.37
Frontal, grup
Exercitarea autocontrolului după model, discuție
Pe tablă (rotativ) răspunde. Elevii efectuează autoexaminare.
Cine a primit aceleași răspunsuri?
Cine nu a fost de acord?
Unde ai facut o greseala?
Întrebări pentru elevi pentru a consolida semnificația geometrică a derivatei:
Numiți liniile care intersectează axa x la un unghi ascuțit.
Numiți liniile pe care // axa Ox.
Numiți dreptele care formează un unghi cu axa x a căror tangentă este un număr negativ.
Reflectarea activității
10.37-10.39
Frontal
Conversaţie
Rezumând lecția.
Ce problemaa apărut în fața noastră în timpul lecției? (a fost necesar să scriem ecuația tangentei, dar nu am știut cum să o facem)
Care sunt obiectivele noastre pentru această lecție? (deduceți ecuația tangentei, aflați cum să scrieți ecuația tangentei pentru o funcție dată la un punct dat)
Ați atins obiectivele lecției?
Câți dintre voi pot spune cu încredere că ați învățat să scrieți ecuația unei tangente?
Cine mai are întrebări? Cu siguranță vom continua să lucrăm pe această temă și, sper, problemele tale vor fi rezolvate 100%!
Teme pentru acasă
10.39-10.40
Notează-ți temele - nr. 255 (vg), 256 (vg), 257 (vg),* , formulă!!!
Căutați în manual temele pentru acasă.
№№ 255(vg), 256(vg) - continuarea lucrărilor de clasă privind dezvoltarea abilității de a scrie ecuația tangentei.
* - sarcina următorului nivel de dificultate pentru cei care doresc să se testeze:
Pe o parabolă y \u003d x 2 + 5x - 16 găsiți punctul în care linia tangentă la ea // 5x+y+4 =0.
Vă mulțumim pentru munca dvs. Lecția s-a terminat.
Tutorialul video „Ecuația tangentei la graficul unei funcții” demonstrează material educațional pentru însușirea temei. În cadrul lecției video este prezentat materialul teoretic necesar formării conceptului de ecuație a tangentei la graficul unei funcții la un punct dat, algoritmul de găsire a unei astfel de tangente, exemple de rezolvare a problemelor folosind teoreticul studiat. sunt descrise materiale.
Tutorialul video folosește metode care îmbunătățesc vizibilitatea materialului. În vizualizare sunt inserate desene, diagrame, sunt date comentarii vocale importante, sunt aplicate animații, evidențierea culorilor și alte instrumente.
Lecția video începe cu prezentarea subiectului lecției și imaginea unei tangente la graficul unei funcții y=f(x) în punctul M(a;f(a)). Se știe că panta tangentei trasate la grafic într-un punct dat este egală cu derivata funcției f΄(a) într-un punct dat. Tot din cursul algebrei se cunoaste ecuatia dreptei y=kx+m. Schematic este prezentată soluția problemei găsirii ecuației tangentei într-un punct, ceea ce se reduce la găsirea coeficienților k, m. Cunoscând coordonatele punctului aparținând graficului funcției, putem găsi m înlocuind valoarea coordonatelor în ecuația tangentei f(a)=ka+m. Din el găsim m=f(a)-ka. Astfel, cunoscând valoarea derivatei într-un punct dat și coordonatele punctului, putem reprezenta ecuația tangentei în acest fel y=f(a)+f΄(a)(x-a).
Urmează un exemplu de întocmire a unei ecuații tangente, urmând schema. Dată o funcție y=x 2 , x=-2. Acceptând a=-2, găsim valoarea funcției în acest punct f(a)= f(-2)=(-2) 2 =4. Determinăm derivata funcției f΄(х)=2х. În acest moment, derivata este egală cu f΄(a)= f΄(-2)=2 (-2)=-4. Pentru a compila ecuația se găsesc toți coeficienții a=-2, f(a)=4, f΄(a)=-4, deci ecuația tangentei y=4+(-4)(x+2). Simplificand ecuația, obținem y \u003d -4-4x.
În exemplul următor, se propune formularea ecuației tangentei de la origine la graficul funcției y=tgx. În acest punct a=0, f(0)=0, f΄(х)=1/cos 2 x, f΄(0)=1. Deci ecuația tangentei arată ca y=x.
Ca o generalizare, procesul de compilare a ecuației tangentei la graficul funcției la un moment dat este formalizat ca un algoritm format din 4 pași:
- Se introduce o desemnare pentru abscisa punctului de contact;
- f(a) se calculează;
- Se determină F΄(х) și se calculează f΄(a). Valorile găsite a, f(a), f΄(a) sunt substituite în formula ecuației tangente y=f(a)+f΄(a)(x-a).
Exemplul 1 ia în considerare compilarea ecuației tangentei la graficul funcției y \u003d 1 / x în punctul x \u003d 1. Folosim un algoritm pentru a rezolva problema. Pentru această funcție în punctul a=1, valoarea funcției f(a)=-1. Derivată a funcției f΄(х)=1/х 2 . În punctul a=1, derivata f΄(a)= f΄(1)=1. Folosind datele obținute, este compilată ecuația tangentei y \u003d -1 + (x-1) sau y \u003d x-2.
În exemplul 2, trebuie să găsiți ecuația tangentei la graficul funcției y \u003d x 3 +3x 2 -2x-2. Condiția principală este paralelismul tangentei și a dreptei y \u003d -2x + 1. În primul rând, găsim panta tangentei, egală cu panta dreptei y \u003d -2x + 1. Deoarece f΄(a)=-2 pentru această linie dreaptă, atunci k=-2 pentru tangenta dorită. Găsim derivata funcției (x 3 + 3x 2 -2x-2) ΄ \u003d 3x 2 + 6x-2. Știind că f΄(a)=-2, găsim coordonatele punctului 3а 2 +6а-2=-2. Rezolvând ecuația, obținem 1 \u003d 0 și 2 \u003d -2. Folosind coordonatele găsite, puteți găsi ecuația tangentei folosind un algoritm binecunoscut. Găsim valoarea funcției în punctele f(a 1)=-2, f(a 2)=-18. Valoarea derivatei în punctul f΄(а 1)= f΄(а 2)=-2. Înlocuind valorile găsite în ecuația tangentei, obținem pentru primul punct a 1 \u003d 0 y \u003d -2x-2, iar pentru al doilea punct a 2 \u003d -2 ecuația tangentei y \u003d -2x- 22.
Exemplul 3 descrie formularea ecuației tangentei pentru desenarea acesteia în punctul (0;3) la graficul funcției y=√x. Decizia se ia conform algoritmului cunoscut. Punctul de atingere are coordonatele x=a, unde a>0. Valoarea funcției în punctul f(a)=√x. Derivata funcției f΄(х)=1/2√х, deci, în punctul dat f΄(а)=1/2√а. Înlocuind toate valorile obținute în ecuația tangentei, obținem y \u003d √a + (x-a) / 2√a. Transformând ecuația, obținem y=x/2√a+√a/2. Știind că tangenta trece prin punctul (0; 3), găsim valoarea lui a. Găsiți a din 3=√a/2. Prin urmare √a=6, a=36. Găsim ecuația tangentei y \u003d x / 12 + 3. Figura prezintă graficul funcției luate în considerare și tangenta dorită construită.
Elevilor li se reamintesc egalitățile aproximative Δy=≈f΄(x)Δx și f(x+Δx)-f(x)≈f΄(x)Δx. Luând x=a, x+Δx=x, Δx=x-a, obținem f(x)- f(a)≈f΄(a)(x-a), deci f(x)≈f(a)+ f΄( a)(x-a).
În exemplul 4, este necesar să găsim valoarea aproximativă a expresiei 2.003 6 . Deoarece este necesar să găsim valoarea funcției f (x) \u003d x 6 în punctul x \u003d 2.003, putem folosi formula binecunoscută, luând f (x) \u003d x 6, a \u003d 2 , f (a) \u003d f (2) \u003d 64, f ΄(x)=6х 5 . Derivată în punctul f΄(2)=192. Prin urmare, 2,003 6 ≈65-192 0,003. După calcularea expresiei, obținem 2,003 6 ≈64,576.
Lecția video „Ecuația tangentei la graficul unei funcții” este recomandată pentru utilizare într-o lecție tradițională de matematică la școală. Pentru un profesor de învățământ la distanță, materialul video va ajuta la explicarea subiectului mai clar. Videoclipul poate fi recomandat pentru a fi luat în considerare de către studenți, dacă este necesar, pentru a-și aprofunda înțelegerea subiectului.
INTERPRETAREA TEXTULUI:
Știm că dacă punctul M (a; f (a)) (em cu coordonatele a și eff din a) aparține graficului funcției y \u003d f (x) și dacă în acest punct se poate desena o tangentă la graficul funcției, nu perpendicular pe abscisa axei, atunci panta tangentei este f "(a) (ef curs de la a).
Să fie date o funcție y = f(x) și un punct M (a; f(a)) și se știe de asemenea că f´(a) există. Să compunem ecuația tangentei la graficul unei funcții date într-un punct dat. Această ecuație, ca și ecuația oricărei drepte care nu este paralelă cu axa y, are forma y = kx + m (y este egal cu ka x plus em), deci sarcina este de a găsi valorile lui coeficienții k și m. (ka și em)
Panta k \u003d f "(a). Pentru a calcula valoarea lui m, folosim faptul că linia dreaptă dorită trece prin punctul M (a; f (a)). Aceasta înseamnă că dacă înlocuim coordonatele lui punctul M din ecuația dreptei, obținem egalitatea corectă : f(a) = ka+m, de unde constatăm că m = f(a) - ka.
Rămâne să înlocuiți valorile găsite ale coeficienților ki și m în ecuația unei linii drepte:
y = kx+(f(a)-ka);
y = f(a)+k(x-a);
y= f(A)+ f"(A) (X- A). ( Y este egal cu eff dintr-o cursă plus ef dintr-un înmulțit cu x minus a).

Am obținut ecuația tangentei la graficul funcției y = f(x) în punctul x=a.
Dacă, să spunem, y \u003d x 2 și x \u003d -2 (adică a \u003d -2), atunci f (a) \u003d f (-2) \u003d (-2) 2 \u003d 4; f´(x) \u003d 2x, deci f "(a) \u003d f´(-2) \u003d 2 (-2) \u003d -4. (atunci eff din a este egal cu patru, eff prim din x este egal cu doi x, ceea ce înseamnă cursa ef de la a este egal cu minus patru)
Înlocuind valorile găsite a \u003d -2, f (a) \u003d 4, f "(a) \u003d -4 în ecuație, obținem: y \u003d 4 + (-4) (x + 2), adică y \u003d -4x -4.
(y este egal cu minus patru x minus patru)
Să compunem ecuația tangentei la graficul funcției y \u003d tgx (y este egal cu tangentei x) la origine. Avem: a = 0, f(0) = tg0=0;
f"(x)= , deci f"(0) = l. Înlocuind valorile găsite a=0, f(a)=0, f´(a) = 1 în ecuație, obținem: y=x.
Ne generalizăm pașii pentru găsirea ecuației tangentei la graficul funcției în punctul x folosind algoritmul.
ALGORITM PENTRU COMPUNEREA ECUAȚIEI FUNCȚIEI tangente la GRAFUL y \u003d f (x):
1) Desemnați abscisa punctului de contact cu litera a.
2) Calculați f(a).
3) Aflați f´(x) și calculați f´(a).
4) Înlocuiți numerele găsite a, f(a), f´(a) în formulă y= f(A)+ f"(A) (X- A).
Exemplul 1. Scrieți ecuația tangentei la graficul funcției y \u003d - în
punctul x = 1.
Soluţie. Să folosim algoritmul, având în vedere că în acest exemplu
2) f(a)=f(1)=-=-1
3) f´(x)=; f´(a)= f´(1)= =1.
4) Înlocuiți cele trei numere găsite: a \u003d 1, f (a) \u003d -1, f "(a) \u003d 1 în formulă. Obținem: y \u003d -1 + (x-1), y \u003d x-2.
Răspuns: y = x-2.
Exemplul 2. Având în vedere o funcție y = x 3 +3x 2 -2x-2. Scrieți ecuația tangentei la graficul funcției y \u003d f (x), paralelă cu dreapta y \u003d -2x +1.
Folosind algoritmul de compilare a ecuației tangente, ținem cont că în acest exemplu f(x) = x 3 +3x 2 -2x-2, dar abscisa punctului de atingere nu este specificată aici.
Să începem să vorbim așa. Tangenta dorită trebuie să fie paralelă cu linia dreaptă y \u003d -2x + 1. Și liniile paralele au pante egale. Prin urmare, panta tangentei este egală cu panta dreptei date: k cas. = -2. Hok cas. = f "(a). Astfel, putem găsi valoarea lui a din ecuația f ´ (a) \u003d -2.
Să găsim derivata funcției y=f(X):
f"(X) \u003d (x 3 + 3x 2 -2x-2)´ \u003d 3x 2 + 6x-2;f„(a) \u003d 3a 2 + 6a-2.
Din ecuația f "(a) \u003d -2, adică. 3а 2 +6а-2\u003d -2 găsim un 1 \u003d 0, un 2 \u003d -2. Aceasta înseamnă că există două tangente care îndeplinesc condițiile problemei: una într-un punct cu abscisă 0, cealaltă într-un punct cu abscisă -2.
Acum puteți acționa conform algoritmului.
1) a 1 \u003d 0 și 2 \u003d -2.
2) f(a 1) = 0 3 +3 0 2 -2∙0-2=-2; f(a2)= (-2) 3 +3 (-2) 2 -2 (-2)-2=6;
3) f „(a 1) = f” (a 2) = -2.
4) Înlocuind valorile a 1 = 0, f (a 1) = -2, f "(a 1) = -2 în formulă, obținem:
y=-2-2(x-0), y=-2x-2.

Înlocuind valorile a 2 \u003d -2, f (a 2) \u003d 6, f "(a 2) \u003d -2 în formulă, obținem:
y=6-2(x+2), y=-2x+2.
Răspuns: y=-2x-2, y=-2x+2.
Exemplul 3. Din punctul (0; 3) trageți o tangentă la graficul funcției y \u003d. Soluţie. Să folosim algoritmul de compilare a ecuației tangente, având în vedere că în acest exemplu f(x) = . Rețineți că aici, ca și în exemplul 2, abscisa punctului de atingere nu este indicată în mod explicit. Cu toate acestea, acționăm conform algoritmului.
1) Fie x = a abscisa punctului de contact; este clar că a > 0.
3) f´(x)=()´=; f´(a) =.
4) Înlocuind valorile a, f(a) = , f "(a) = în formula
y \u003d f (a) + f "(a) (x-a), primim:
Prin condiție, tangenta trece prin punctul (0; 3). Înlocuind valorile x = 0, y = 3 în ecuație, obținem: 3 = , iar apoi =6, a =36.
După cum puteți vedea, în acest exemplu, abia la pasul al patrulea al algoritmului am reușit să găsim abscisa punctului de atingere. Înlocuind valoarea a =36 în ecuație, obținem: y=+3
Pe fig. Figura 1 prezintă o ilustrare geometrică a exemplului considerat: este trasat un grafic al funcției y \u003d, este trasată o linie dreaptă y \u003d +3.
Răspuns: y = +3.
Știm că pentru funcția y = f(x), care are o derivată în punctul x, egalitatea aproximativă este valabilă: Δyf´(x)Δx
sau, mai detaliat, f(x+Δx)-f(x) f´(x) Δx (ef din x plus delta x minus ef din x este aproximativ egal cu ef cursa de la x la delta x).
Pentru comoditatea unui raționament suplimentar, schimbăm notația:
în loc de x vom scrie A,
în loc de x + Δx vom scrie x
în loc de Δx vom scrie x-a.
Atunci egalitatea aproximativă scrisă mai sus va lua forma:
f(x)-f(a)f´(a)(x-a)
f(x)f(a)+f´(a)(x-a). (ef din x este aproximativ egal cu eff dintr-o cursă plus ef din a, înmulțit cu diferența dintre x și a).

Exemplul 4. Aflați valoarea aproximativă a expresiei numerice 2.003 6 .
Soluţie. Vorbim despre găsirea valorii funcției y \u003d x 6 în punctul x \u003d 2.003. Să folosim formula f(x)f(a)+f´(a)(x-a), având în vedere că în acest exemplu f(x)=x 6 , a = 2,f(a) = f(2) = 2 6 =64; x \u003d 2,003, f "(x) \u003d 6x 5 și, prin urmare, f" (a) \u003d f "(2) \u003d 6 2 5 \u003d 192.
Ca rezultat, obținem:
2,003 6 64+192 0,003, i.e. 2,003 6 = 64,576.
Dacă folosim un calculator, obținem:
2,003 6 = 64,5781643...
După cum puteți vedea, acuratețea aproximării este destul de acceptabilă.