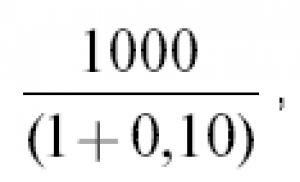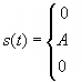C ecuații diferențiale ordinare prin metoda Picard. Rezolvarea ecuațiilor diferențiale obișnuite. Soluții numerice ale ODE. Metodele Euler

Scopul lucrării: să formeze înțelegerea studenților cu privire la aplicarea telecomenzii în diverse domenii; pentru a insufla capacitatea de a rezolva problema Cauchy pentru telecomanda la" = f(X,y) pe segmentul [ A, b] pentru o condiție inițială dată la 0 = f(X 0) metodele Picard, Euler, Runge-Kutta, Adams; dezvolta abilitatile de verificare a rezultatelor obtinute cu ajutorul programelor aplicative.

metoda Picard

Exemplul 5.1.

: la h= 0,1 prin metoda Picard cu un pas h.

În raport, prezentați: progresul lucrării, programul - funcția, eroarea, o ilustrare grafică a soluției.

Soluţie.

1. Introduceți datele (Fig. 5.1)

A= 1,7 b= 2,7

h = 0,1

y 0 = 5,3 i = 0..n

Fig.5.1. Setarea datelor inițiale

2. Setăm o funcție care returnează valorile primei derivate în raport cu variabila la(fig.5.2).

f deriva( y) =

Fig.5.2. O funcție care returnează valoarea primei derivate a unei funcții

3. Compuneți o funcție care returnează soluția DE prin metoda

Picard. Aici: f- funcția originală; f deriv –

Derivată a unei funcții în raport cu la; A,b- capete ale segmentului; h- Etapa; la 0 –

valoarea initiala a variabilei la.

4. Aflați soluția DE prin metoda Picard (Fig. 5.3).

fnPikan(fn, fn derivă, a, b, h, y0)=

Orez. 5.3. Specificarea unei funcții care returnează o soluție la DE

Metoda Picard (fișier fnPikar.mcd)

fnPikar(f, f derivă, a, b, 0,1, y0) =

	7.78457519486 10 -11
	5,3
	5,46340155616
	5,62650688007
	5,78947945853
	5,95251650231
	6,11584391144
	6,27971330675
	6,44440084325
	6,61020759752
	6,77746140952
	6,94652015221

Orez. 5.4. Găsirea unei soluții numerice a DE prin metoda Picard

Metoda Euler și modificările acesteia

Exemplul 5.2.

la(1.7) = 5.3 și pasul de integrare h= 0,1 prin metoda Euler și metoda Euler îmbunătățită cu pași hȘi h/2.

Soluţie.

Cursul rezolvării problemei prin metoda Euler este prezentat în Fig. 5,5 - 5,7.

a = 1,7 b = 2,7 y0 = 5,3

y 0 = y0 x i = a + ih h2 = 0,05

Fig5.5. Fragment de foaie de lucru Mathcad cu soluție

ecuații prin metoda Euler cu un pas hȘi h/2 și grafic

vizualizarea metodei Euler.

1. Să creăm un program care implementează metoda Euler (Fig.

Fig.5.6. Lista de programe care implementează metoda Euler

2. Obținem soluția DE prin metoda Euler (Fig. 5.7.).

ES h = eyler(f, a, b, h, y0)

ES h2 = eyler(f, a, b, , y0)

Orez. 5.7. Găsirea unei soluții numerice a DE prin metoda Euler

Notă

Compuneți singur funcția returnând soluția DE prin metoda Euler îmbunătățită.

Orez. 5.8. Decizia telecomenzii printr-o metodă îmbunătățită

Euler cu trepte hȘi h/2

5.3. Metoda Runge–Kutta

În practică, metoda Runge-Kutta de ordinul al patrulea este cel mai des folosită.

Exemplul 5.3.

Rezolvați problema Cauchy pentru DE pe un segment pentru un NU dat la(1.7) = 5.3 și pasul de integrare h= 0,1 prin metoda Runge-Kutta de ordinul al patrulea cu un pas hși 2 h.

În raport, prezentați: progresul lucrării, programul, funcția, eroarea, o ilustrare grafică a soluției și o estimare a erorii de aproximare.

Soluţie.

1. Introduceți datele sarcinii (Fig. 5.9).

A = 1,7 b = 2,7

h = 0,1

y 0 = 5,3

i= 0..n

Fig.5.9. Setarea datelor inițiale

2. Să compunem o funcție care returnează soluția DE de ordinul întâi prin metoda Runge-Kutta. Aici: fn este funcția dată; A, b- capete ale segmentului; h- Etapa; y 0 este valoarea inițială a funcției.

3. Să găsim soluția DE de ordinul întâi folosind funcțiile încorporate ale Mathcad (Fig. 5.10).

RK h = fnRungeKutta(f, a, b, h, y0)

RK 2h = fnRungeKutta(f, a, b, 2h, y0)

Orez. 5.10. Listarea unei funcții care returnează o valoare numerică

Soluție DE prin metoda Runge–Kutta

metoda Adams

Exemplul 5.4.

Rezolvați problema Cauchy pentru DE pe un segment pentru un NU dat la(1.7) = 5.3 și pasul de integrare h= 0,1 metoda Adams cu pas h.

În raport, trimiteți: un cont manual, un program - o funcție, o eroare, o ilustrare grafică a soluției și o estimare a erorii de aproximare.

Soluţie.

1. Găsiți primele patru numere folosind formula Runge-Kutta (Fig. 5.11).

y i = fnRungeKutta(f, a, b, h, y0) i

Orez. 5.11. Calculul primelor patru valori ale soluției numerice folosind formula Runge-Kutta

2. Să compunem o funcție care implementează metoda Adams (Fig. 2.10.3). Aici A, b- capete ale segmentului; y 1 – valoarea inițială a funcției; h- Etapa.

Orez. 5.12. O funcție care returnează o soluție numerică

Metoda DE de Adams

3. O ilustrare grafică a soluției DE prin diferite metode este prezentată în fig. 5.13.

Orez. 5.13. Vizualizarea soluției DE prin diferite metode

Întrebări înrudite

1. Ce înseamnă să rezolvi problema Cauchy pentru un DE de ordinul întâi?

2. Interpretarea grafică a soluției numerice a DE.

3. Care sunt metodele de rezolvare a DE în funcție de

forma de solutie?

4. Care este esența principiului compresivului

cartografii?

5. Formula recursiva a metodei Picard.

6. Care este esența metodei Euler întrerupte?

7. Aplicație, ce formule vă permite să obțineți valori

funcția dorită folosind metoda Euler?

8. Interpretarea grafică a metodei Euler și

metoda Euler îmbunătățită. Care este diferența lor?

9. Care este esența metodei Runge-Kutta?

10. Cum să determinați numărul de cifre corecte dintr-un număr,

care este soluția DE prin metoda Euler,

metoda îmbunătățită a lui Euler, Picard, Runge–

Misiunea pentru lucru de laborator nr. 5

Sarcina 5.1.

Rezolvați problema Cauchy pentru DE y’ = f(X, y) pe intervalul [ A, b] la un NU dat la(A) = Cuși etapa de integrare h(parametrii inițiali sunt dați în Tabelul 2.10.1):

1) metoda Euler și metoda Euler îmbunătățită cu un pas hȘi h/2;

2) prin metoda Runge–Kutta cu un pas hși 2 h;

3) metoda Adams;

4) prin metoda Picard.

Soluția trebuie să conțină: progresul lucrării, programul metodei, soluția grafică a ecuației și estimarea erorii de aproximare. În numere, lăsați 5 cifre după virgulă.

Tabelul 5.1. Opțiuni de sarcini pentru munca independentă

№	f( X, y)	[A, b]	y 0	h
	3X 2 + 0,1hu		la(0) = 0,2	0,1
	0,185(X 2 + cos(0,7 X)) + 1,843y		la(0,2) = 0,25	0,1
			la(1,6) = 4,6	0,1
			la(0,2) = 1,1	0,1
			la(1,4) = 2,5	0,1
			la(1,7) = 5,3	0,1
			la(2,6) = 3,5	0,2
			la(2) = 2,3	0,1
	1,6 + 0,5y2		la(0) = 0,3	0,1
			la(1,8) = 2,6	0,1
			la(2,1) = 2,5	0,1
	e 2X + 0,25y 2		la(0) = 2,6	0,05
		[- 2; -1]	la(-2) = 3	0,1
	0,133 ( x2+ păcat(2 X)) + 0,872y		la(0,2) = 0,25	0,1
	păcat( X + y) +1,5		la(1,5) = 4,5	0,1
			la(0,4) = 0,8	0,1
	2,5X+ cos( y + 0,6)		la(1) = 1,5	0,2
	cos(1,5 y +X) 2 + 1,4		la(1) = 1,5	0,1
			la(1,5) = 2,1	0,05
	cos y + 3X		la(0) = 1,3	0,1
	cos(1,5 X – y 2) – 1,3	[-1; 1]	la(-1) = 0,2	0,2
			la(1,6) = 4,6	0,1
	e -(y – 1) + 2X		la(0) = 0,3	0,05
	1 + 2y păcat X – y 2		la(1) = 0	0,1
			la(0) = 0	0,1
	0,166(X 2 + sin(1,1 X)) + 0,883y		la(0,2) = 0,25	0,1
			la(1,7) = 5,6	0,1
			la(1,4) = 2,5	0,1
			la(0,6) = 0,8	0,1
			la(1) = 5,9	0,1
	1 + 0,8y păcat X - 2y 2		la(0) = 0	0,1
			la(0,5) = 1,8	0,1
			la(1,2) = 1,8	0,1
	1 + 2,2 sin X + 1,5y 2		la(0) = 0	0,1
			la(0) = 0	0,1
			la(0) = 0	0,1
			la(0) = 0	0,1
	0,2X 2 + y 2		la(0) = 0,8	0,1
	X 2+y		la(0) = 0,4	0,1
	X y + 0,1y 2		la(0) = 0,5	0,1

Literatură

Literatura principală:

Alekseev G.V., Voronenko B.A., Lukin N.I. Metode matematice în

Ingineria alimentară: manual. - Sankt Petersburg: „Lan”, 2012. - 212 p.

Alekseev G.V. Metode matematice în inginerie: Metoda de studiu. indemnizatie. - Sankt Petersburg: NRU ITMO; IHiBT. 2012. - 39 p.

Alekseev G.V., Kholiavin I.I. Modelare și optimizare economico-matematică numerică: manual pentru universități, GIEFPT, 2011, 211 p.

Makarov E.G. Mathcad: Tutorial. - Sankt Petersburg: Peter, 2009. - 384 p.

literatură suplimentară:

Porshnev S.V., Belenkova I.V. Metode numerice bazate pe Mathcad. -

Sankt Petersburg: BHV-Petersburg, 2005. - 464 p.

Agapiev B.D., Belov V.N., Kesamanly F.P., Kozlovsky V.V., Markov S.I. Prelucrarea datelor experimentale: Proc. indemnizație / SPbGTU. SPb., 2001.

Gorelova G.V. Teoria probabilității și statistică matematică în exemple și sarcini folosind Excel. – M.: Phoenix, 2005. – 476 p.

Adler Yu.P., Markov E.V., Granovsky Yu.V. Planificarea unui experiment în căutarea condițiilor optime.-M .: Nauka, 1976

Asaturyan V.I. Teoria planificării experimentelor.-M .: Radio și comunicare, 1983

Brodsky V.Z. Introducere în planificarea factorială a experimentului - M .: Nauka, 1976

Demidenko E.Z. Regresia liniară și neliniară.-M.: Finanțe și statistică, 1981

Krasovsky G.I., Filaretov G.F. Planificarea experimentului.-Minsk: BSU, 1982

Markova E.V., Lisenkov A.N. Planuri combinatorii în sarcinile unui experiment multifactorial - M .: Nauka, 1979

Frolkis V.A. Optimizare liniară și neliniară.-Sankt Petersburg. 2001. 306 p.

Kuritsky B.Ya. Căutați soluții optime folosind Excel 7.0.-St. Petersburg: BHV, 1997, 384c

software și resurse de internet:

http://www.open-mechanics.com/journals - Procese și aparate de producție alimentară

http://www.spbgunpt.narod.ru/ur_gigm.htm - Mecanica fluidelor și gazelor, hidraulice și mașini hidraulice

http://elibrary.ru/defaultx.asp - biblioteca electronică științifică „Biblioteca”

Introducere

1. Lucrări de laborator Nr. 1: Teoria calculelor aproximative

1.1. Erori absolute și relative

1.2. Eroare de rotunjire

1.3. Erori aritmetice

1.4. Erori ale funcţiilor elementare

1.5. Calea frontierelor

1.6. Problema inversă a teoriei erorilor

1.7. Întrebări înrudite

1.8. Sarcini pentru munca de laborator Nr. 1

2. Lucrări de laborator Nr. 2: Metode numerice de soluţionare

ecuații scalare

1.1. metoda acordurilor

1.2. Metoda tangentei

1.3. Metodă simplă de iterație

1.4. Întrebări înrudite

1.5. Sarcini pentru munca de laborator Nr.2

3. Lucrare de laborator Nr. 3: Metode numerice de rezolvare a sistemelor

ecuații neliniare

3.1. metoda lui Newton

3.2. Întrebări înrudite

3.3. Misiunea pentru munca de laborator nr. 3

4. Laboratorul #4: Integrare numerică

4.1. Metoda dreptunghiului

4.2. Metoda Simpson

4.3. Metoda trapezoidală

4 .4. Metoda Monte Carlo

4.5. Întrebări înrudite

4.6. Misiunea pentru lucru de laborator nr. 4

5. Laboratorul #5: Rezolvarea ecuațiilor diferențiale obișnuite

5.1. metoda Picard

5.2. Metoda Euler și modificările acesteia

5.3. Metoda Runge–Kutta

Biletul numărul 5.3. Modelul general de sistem al obiectului de control. Caracteristicile grupurilor de variabile. Decizie de management din punctul de vedere al modelului. Problema variabilelor de „ieșire” și modalități de a o rezolva

Această metodă este un reprezentant al clasei de metode aproximative

Ideea metodei este extrem de simplă și se rezumă la o procedură

aproximări pentru rezolvarea ecuaţiei integrale, la care

este dată ecuația diferențială inițială.

Să se stabilească problema Cauchy

,

Integram ecuatia scrisa

. (5.2)

Procedura de aproximări succesive ale metodei Picard este implementată conform următoarei scheme

, (5.3)

Exemplu . Rezolvați ecuația Picard

,

Rezolvarea acestei ecuații nu este exprimată în termeni de funcții elementare.

,

Se poate observa că pentru , seria converge rapid. Metoda este convenabilă dacă integralele pot fi luate analitic.

Să demonstrăm convergența metodei Picard. Lasă unele limitate

regiunea, partea dreaptă este continuă și, în plus, satisface condiția Lipschitz față de variabilă, i.e.

unde este o constantă.

Datorită delimitării regiunii, inegalităților

Scădem formula (5.2) din (5.3), obținem pentru modulele din dreapta și din stânga

,

.

În final, folosind condiția de continuitate Lipschitz, obținem

, (5.4)

unde este eroarea soluției aproximative.

Aplicarea succesivă a formulei (5.4) la oferă următorul lanț de relații, ținând cont de faptul că

,

,

.

Deoarece , atunci noi avem

.

Înlocuind cu formula Stirling, obținem în final o estimare pentru eroarea soluției aproximative

. (5.5)

Din (5.4) rezultă că pentru modulul de eroare, i.e.

soluția aproximativă converge uniform către cea exactă.

5.2.2. Metode Runge-Kutta

Aceste metode sunt numerice.

În practică, sunt utilizate metodele Runge-Kutta, oferind post-

scheme de diferențe de roi (metode) de diverse ordine de precizie. Cel mai

scheme (metode) comune de ordinul doi și al patrulea. Noi și ei

luați în considerare mai jos.

Să introducem mai întâi câteva noțiuni și definiții. plasă pe

segmentul este un set fix de puncte ale acestui segment.

Funcția definită în aceste puncte se numește funcție grilă.

Coordonatele punctelor satisfac condițiile

Punctele sunt nodurile grilei. O grilă uniformă este un set de puncte

, ,

unde este distanța dintre grile.

La rezolvarea ecuațiilor diferențiale printr-o metodă aproximativă, problema convergenței este cea principală. Așa cum este aplicat metodelor de diferență, conceptul de convergență pentru este în mod tradițional mai comun. Să notăm valorile funcției grilei ca fiind valorile soluției exacte a ecuației diferențiale (5.1) la nodul - (sunt valori aproximative). Convergența înseamnă următoarele. Fixăm un punct și construim un set de grile în așa fel încât (în care). Atunci se consideră că metoda numerică converge într-un punct dacă

la ,. Metoda converge pe un segment dacă acesta converge în fiecare punct. Se spune că o metodă are ordinul al treilea al preciziei dacă un număr poate fi găsit astfel încât la.

În continuare, introducem conceptul de eroare reziduală sau de aproximare a unei ecuații diferențiale care înlocuiește o ecuație diferențială dată pe soluția ecuației originale, adică, discrepanța este rezultatul înlocuirii soluției exacte a ecuației (5.1) în ecuația diferențelor. De exemplu, (5.1) poate fi înlocuită cu următoarea ecuație de diferență simplă

, .

Apoi discrepanța este determinată de următoarea expresie

.

Soluția aproximativă nu coincide, în general, cu , deci discrepanța în al-lea punct nu este egală cu zero. Se introduce următoarea definiție: metoda numerică aproximează ecuația diferențială inițială dacă , și are ordinul al treilea de precizie dacă .

Se demonstrează că ordinea acurateței metodei numerice de rezolvare a unei ecuații diferențiale coincide cu ordinea aproximării în ipoteze destul de generale.

Acum să trecem la analiza schemelor Runge-Kutta. Să ne întoarcem mai întâi la

scheme de ordinul doi de precizie.

Folosind formula Taylor, rezolvarea ecuației diferențiale

(5.1) poate fi reprezentat ca

, (5.6)

unde este indicat, ,.

Rețineți că conform (5.1) ,.

derivat după cum urmează

,

unde sunt cantități necunoscute. Lăsa

Să notăm valoarea aproximativă a soluției la nodul cu numărul prin (această soluție va fi obținută după ce restrângem seria la termeni cu un ordin nu mai mare decât al doilea).

Parametrii introduși aici urmează a fi determinați.

Extindem partea dreaptă într-o serie Taylor și aducem termeni similari, obținem

rand pe rand

Condiția pentru alegerea parametrilor și stabilim proximitatea expresiei

relația (5.7) cu seria (5.6), apoi

, ,.

Un parametru rămâne liber. Să fie atunci

, ,

iar în final din (5.7), ținând cont de relațiile găsite pentru și

Relația (5.8) descrie o familie cu un parametru de formule Runge-Kutta cu doi termeni.

În literatura specială, se demonstrează că dacă este continuă și mărginită împreună cu derivatele sale secundare, atunci soluția aproximativă a schemei (5.8) converge uniform către soluția exactă cu o eroare. , adică schema (5.8) are al doilea ordin de precizie.

În practica calculelor, formulele (5.8) sunt utilizate pentru valorile parametrului ,.

Din (5.8) deducem

Aplicarea formulei (5.9) se reduce la următoarea secvență de pași:

1. Valoarea funcției este calculată aproximativ (conform schemei cu linii întrerupte)

2. Se determină panta curbei integrale în punctul ().

3. Se găsește valoarea medie a derivatei funcției la pas

4. Valoarea funcției este calculată la nodul ()-al-lea

Această schemă are o denumire specială „predictor-corector”.

Conform (5.8), obținem

Problema este rezolvată prin următorii pași:

1. Se calculează valoarea funcției la jumătatea nodului

.

2. Se determină valoarea derivatei la nod

.

3. Valoarea funcției se găsește în nodul ()-al-lea

În plus față de schemele cu doi termeni considerate mai sus, schemele Runge-Kutta de ordinul al patrulea de precizie sunt utilizate pe scară largă în practica calculelor. Formulele corespunzătoare sunt date mai jos fără derivare.

(5.10)

Schemele cu un număr mare de membri practic nu sunt utilizate. Cinci-

formulele membre oferă al patrulea ordin de precizie, formulele cu șase termeni au ordinul al șaselea, dar forma lor este foarte complicată.

Erorile schemelor Runge-Kutta de mai sus sunt determinate de maxim

valorile derivatelor corespunzătoare.

Este ușor de obținut o estimare a erorilor pentru cazul special al dreptului

părți ale unei ecuații diferențiale

.

În acest caz, soluția ecuației poate fi redusă la cuadratura și

toate schemele de soluții ale diferențelor sunt convertite în formule de integrare numerică

rătăcire. De exemplu, schema (5.9) ia forma

,

adică are forma formulei trapezoidale, iar schema (5.10) trece în schemă

care este formula lui Simpson cu pasul .

Estimările de eroare majoră pentru formulele trapezoid și Simpson sunt cunoscute (vezi Secțiunea 3.2). Din (3.4) și (3.5) se poate observa că acuratețea schemelor Runge-Kutta este destul de mare.

Alegerea uneia sau alteia dintre schemele de mai sus pentru rezolvarea unei probleme specifice

dacha este determinată de următoarele considerații. Dacă funcția în

partea dreaptă a ecuației este continuă și mărginită, precum și continuă și

derivatele sale a patra sunt limitate, atunci se obține cel mai bun rezultat

la utilizarea schemei (5.10). În cazul în care funcţia

nu are derivatele de mai sus, de ordinul limitativ (al patrulea).

schema (5.10) nu poate fi realizată și se dovedește a fi oportună

folosind scheme mai simple.

Pe lângă schemele Runge-Kutta, metodele în mai multe etape prezintă un interes practic, care pot fi descrise prin următorul sistem de ecuații

Unde , a - coeficienți numerici, ,.

Conform acestei ecuații, calculul începe cu . În acest caz, obținem o relație de formă

acestea. pentru a începe să numărați trebuie să aveți valori inițiale. Aceste valori trebuie calculate printr-o altă metodă, de exemplu, metoda Runge-Kutta.

Dintre metodele cu mai multe etape, cea mai comună este metoda Adams, a cărei schemă de implementare rezultă din (5.11) cu si pentru :

.

Pentru , metoda Adams se dovedește a fi explicită, în timp ce pentru , este implicită.

Vom lua în considerare o ecuație diferențială obișnuită (ODE) de ordinul întâi

cu starea initiala

y(x 0) \u003d y 0, (2)

unde f(x) este o funcție dată, în cazul general, neliniară a două variabile. Vom presupune că pentru o problemă dată (1)-(2), numită problemă inițială sau problema Cauchy, sunt îndeplinite cerințele care asigură existența și unicitatea pe segmentul [x 0 ,b] a soluției sale y=y (X).

În ciuda simplității exterioare a ecuației (1), rezolvați-o analitic, i.e. se poate gasi o solutie generala y=y(x, C) pentru a extrage apoi din ea curba integrala y=y(x) care trece printr-un punct dat (x 0; y 0) doar pentru unele tipuri speciale de astfel de ecuații. Prin urmare, ca și în problema calculării integralelor legate de (1)-(2), trebuie să ne bazăm pe metode aproximative pentru rezolvarea problemelor inițiale pentru EDO, care pot fi împărțite în trei grupuri:

1) metode analitice aproximative;

2) metode grafice sau computer-grafice;

3) metode numerice.

Metodele primului grup le includ pe cele care permit să se găsească imediat o aproximare a soluției y(x) sub forma unei funcții „bune” φ (X). De exemplu, binecunoscutul metoda seriei de putere, una dintre implementările cărora se bazează pe reprezentarea funcției dorite y(x) de către un segment din seria Taylor, unde coeficienții Taylor care conțin derivate de ordin superior se găsesc prin diferențierea succesivă a ecuației (1) însăși. Un alt reprezentant al acestui grup de metode este metoda aproximărilor succesive, a cărei esență este prezentată mai jos.

Nume metode grafice vorbește despre o reprezentare aproximativă a soluției dorite y(x) pe interval sub formă de grafic, care poate fi construită după anumite reguli legate de interpretarea grafică a acestei probleme. Interpretarea fizică sau, poate, ar fi mai corect să spunem, a problemelor inițiale pentru anumite tipuri de ecuații stă la baza metodelor grafice computerizate de soluție aproximativă. Realizând procesele electrice date la nivel fizic și tehnic, pe ecranul osciloscopului se observă comportamentul soluțiilor ecuațiilor diferențiale care descriu aceste procese. Modificarea parametrilor ecuației duce la o modificare adecvată a comportamentului soluțiilor, care stă la baza calculatoarelor analogice specializate (ACM).

În sfârșit, cele mai semnificative în prezent, caracterizate prin dezvoltarea și pătrunderea rapidă în toate sferele activității umane a calculului digital, sunt metodele numerice de rezolvare a ecuațiilor diferențiale, care presupun obținerea unui tabel numeric cu valorile aproximative y i ale soluției dorite y (x) pe o anumită grilă
valorile argumentului x. Aceste metode vor face obiectul următoarei discuții. Ce să faceți cu valorile numerice rezultate ale soluției depinde de formularea aplicată a problemei. Dacă vorbim despre găsirea doar a valorii lui y(b), atunci punctul b este inclus ca punct final în sistemul de puncte calculate x i și toate valorile aproximative y i ≈ y(x i), cu excepția ultimei , participă doar ca intermediari, adică nu necesită memorare sau prelucrare. Dacă trebuie să aveți o soluție aproximativă y(x) în orice punct x, atunci pentru aceasta puteți aplica oricare dintre metodele de aproximare a funcțiilor tabelului discutate mai devreme la tabelul numeric rezultat al valorilor y i, de exemplu, interpolarea sau interpolare spline. Sunt posibile și alte utilizări ale datelor numerice despre soluție.

Să atingem o metodă analitică aproximativă pentru rezolvarea problemei inițiale (1)-(2), în care soluția dorită y \u003d y (x) într-o vecinătate dreaptă a punctului x 0 este limita șirului de funcţiile y n (x) obţinute într-un anumit mod.

Integram părțile din stânga și dreapta ale ecuației (1) în limitele de la x 0 la x:

Prin urmare, ținând cont de faptul că una dintre antiderivatele pentru y"(x) este y(x), obținem

sau, folosind condiția inițială (2),

(3)

Astfel, această ecuație diferențială (1) cu condiția inițială (2) a fost transformată într-o ecuație integrală (aici, funcția necunoscută intră sub semnul integral).

Ecuația integrală rezultată (3) are forma unei probleme de punct fix pentru operator
Formal, metoda iterațiilor simple poate fi aplicată acestei probleme

considerat suficient de detaliat în raport cu sistemele de ecuaţii algebrice şi transcendentale liniare şi neliniare. Luând ca funcție inițială y 0 (x) constanta y 0 specificată în (2), conform formulei (4) la n=0 găsim prima aproximare

Înlocuirea lui în (4) cu n=1 dă a doua aproximare

etc. Astfel, această metodă aproximativ-analitică, numită metoda aproximărilor succesive sau metoda Picard, este definită prin formula

(5)

unde n=0,1, 2,... și y 0 (x)=y 0 .

Remarcăm două caracteristici ale metodei lui Picard de aproximări succesive, care pot fi clasificate drept negative. În primul rând, din cauza problemelor bine-cunoscute cu găsirea eficientă a antiderivatelor, metoda (5) este rareori implementată în forma sa pură. În al doilea rând, după cum se poate observa din afirmația de mai sus, această metodă ar trebui considerată locală, potrivită pentru aproximarea soluției într-o mică vecinătate dreaptă a punctului inițial. Metoda lui Picard este mai importantă pentru a demonstra existența și unicitatea unei soluții la problema Cauchy decât pentru a o găsi în practică.

Lecția numărul 17. Metode Euler.

țintă - pentru a familiariza elevii cu metodele lui Euler de rezolvare a problemei Cauchy pentru ecuaţii diferenţiale ordinare.

Reamintim binecunoscutele teoreme Picard și Peano privind existența și unicitatea unei soluții la o problemă dată (problema Cauchy).

Teorema PEANO afirmă că o soluție la problema Cauchy există în vreo vecinătate a punctului X o dacă funcția f(x,Y) este continuă în vecinătatea punctului (X 0 ,Y 0).

Teorema PICARD spune că dacă nu numai funcția f (x, Y), ci și derivata ei parțială f "y (x, Y) este și continuă în vecinătatea punctului (X 0, Y 0), atunci soluția a problemei Cauchy este unică pe un anumit segment, care conține punctul X 0 .

Dovada teoremei lui Picard decurge din principiul general al mapărilor de contracție, nu este ușoară, dar are un avantaj semnificativ – este constructivă. Mai mult decât atât, șirul de funcții Y n (x), care este construit în ea, converge către soluția uniform pe segmentul cu viteza unei progresii geometrice. În metoda Picard, succesiunea de funcții Y n (x) este construită după formula recursivă:

Pentru n= 0,1,2,...,

iar aproximarea zero este constanta Y 0: Y 0 (х)ºY 0 .

Pentru a înțelege originea acestei formule recurente, observăm că ecuația integrală

este echivalentă cu problema Cauchy inițială, deoarece orice funcție Y (x), care este soluția sa, satisface condiția inițială Y (X o) \u003d Y o și ecuația Y "(x) \u003d f (x, Y ( x)) și invers.

Întrebare: De ce este cu adevărat așa?

Exemplul 4.1 Să folosim metoda Picard pentru a rezolva ecuația Y"=Y cu condiția inițială Y(0)=1. Această problemă este echivalentă cu găsirea unei soluții la ecuația integrală Y=1+òY(t)dt.

Ca o aproximare inițială, luăm funcția Y o =1.

Atunci Y 1 =1+òY o (t)dt= 1+òdt= 1+x.

Y 3 = 1+òY 2 (t)dt= 1+ò(1+t+t 2/2)dt= 1+x+x 2/2+x 3/6.

Vă puteți asigura că Y n = 1+х+x 2 /2+ ... +x n /n!.

Exercițiul 4.1 Demonstrați riguros ultima egalitate folosind principiul inducției matematice.

Exercițiul 4.2 În exemplul 4.1, găsiți soluția exactă Y(X) și estimați rata de convergență uniformă Y n (x) -> Y(X) pe segmentul .

În general, metodele aproximative pentru rezolvarea ecuațiilor diferențiale obișnuite pot fi împărțite în 3 tipuri:

· analitic, permițând obținerea unei soluții aproximative Y(x) sub forma unei formule,

· grafic, făcând posibilă aproximarea graficului soluției Y(x), adică. curba integrala,

· numeric, în urma căruia se obține un tabel de valori aproximative ale funcției Y(x),

deşi o astfel de împărţire este oarecum arbitrară.

Pe lângă metoda Picard, metodele analitice includ și

metoda de extindere a funcției necunoscute Y(x) într-o serie,

pe care ne vom concentra acum.

Să scriem expansiunea formală a lui Y(X) într-o serie Taylor în punctul a:

Această egalitate include derivatele funcției necunoscute Y(X) în punctul a, totuși, în acest punct, folosind condițiile problemei, putem găsi succesiv orice număr de derivate și obținem aproximarea necesară a soluției. . În general, arată astfel: Y o (a) = Y (a) = Y o; Y "(a) \u003d f (a, Y (a)) \u003d f (a, Y o)

Diferențiând ecuația dată nouă față de X, obținem

Y "" (X) \u003d f " x (x, Y (x)) + f" y (x, Y (x)) * Y "(x), de unde Y "" (a) \u003d f " x (a ,Yo)+f" y (a,Yo)*f(a,Yo).

În mod similar, obținem valorile derivatelor a treia și ulterioare la punctul a - diferențiem de numărul necesar de ori ecuația inițială și înlocuim valorile derivatelor obținute mai devreme la punctul a.

Exemplul 4.2 Să scriem primii termeni ai expansiunii într-o serie a funcției Y(x) care satisface ecuația Y "=2xY și condiția inițială Y(0)=1.

Y"""(x)=2 Y"(x)+2 Y"(x)+2x*Y""(x)= 4Y"(x)+2xY""(x), de unde Y"""( 0)=0.

Y (4) (x)=4Y""(x)+2xY"""(x), de unde Y (4) (0)=6.

Obținem o soluție aproximativă Y(x)»1+x 2 +0.5x 4 .

Exercițiul 4.3 Folosind formula Leibniz pentru a găsi derivata n-a a produsului funcțiilor, scrieți expansiunea funcției căutate în Exemplul 4.2 într-o serie Taylor.

Exercițiul 4.4 Găsiți soluția exactă din Exemplul 4.2 și evaluați calitatea aproximării din Exemplul 4.2 pe segmentul [-0.5,0.5].

Metodele descrise mai sus nu sunt adesea folosite în practică, deoarece în metoda Picard la fiecare pas este necesar să se calculeze integrala, ceea ce complică calculele și înrăutățește acuratețea, iar în metoda de extindere a seriei este extrem de dificilă formalizarea procesului. de a găsi derivate de ordin înalt în oricare dintre limbi și cu un număr mic de termeni de expansiune, această metodă oferă o aproximare bună doar în apropierea punctului a.

Printre GRAFICI ia în considerare

1
18.01.2018

Formularea problemei
Diferenţial
ecuații
stabilesc legături între independente
variabilele, funcțiile dorite și acestea
derivate. Dacă funcția necesară
depinde de o variabilă, atunci
se numește ecuație diferențială
comun.

Formularea problemei
De exemplu, condiția de echilibru pentru un mediu elastic
este descris de diferenţialul obişnuit
ecuaţie:
dTx
fx 0
dx
Tx - componenta mecanica
tensiuni, F - care acționează asupra
forță medie continuă per
unitate de masă
Aici funcția dorită (mecanică
tensiune) T(x) depinde de o variabilă
x (coordonată).

Formularea problemei

Dacă funcţia dorită depinde de
variabile multiple, ecuație diferențială
va fi o ecuație cu diferență parțială.
De exemplu, mișcarea unui mediu elastic poate fi descrisă
ecuație cu diferență parțială:
2u x Tx
2
t
X
ux este deplasarea mediului, ρ este densitatea
mediu, Tx este componenta tensiunii
În această ecuație, funcția u(t,x) depinde de timp
(t) și direcția de deplasare medie (x).

Formularea problemei
Ecuații diferențiale obișnuite
(ODE) se numesc ecuații care conțin unul sau
mai multe derivate ale funcției dorite y = y(x):
F (x, y, y,..., y(n)) 0 ,
unde x este o variabilă independentă.
Cel mai înalt ordin al lui n din ecuație
derivata se numeste ordinul diferentialului
ecuații.
De exemplu:
F (x, y, y ") 0 ecuație de ordinul întâi;
F (x, y, y " , y") 0 ecuație de ordinul doi

Formularea problemei
Din notația generală a ecuației diferențiale
derivata poate fi exprimată explicit:
y "f(x, y),
y" f(x, y, y")
Ecuația derivată are un infinit
multe solutii. Pentru a obține singurul
soluțiile trebuie să precizeze suplimentar
condiţii care trebuie îndeplinite de dorit
solutii.

Formularea problemei
În funcție de tipul de condiții
luați în considerare trei tipuri de probleme pentru care a fost dovedit
existența și unicitatea soluțiilor.
Primul tip este problemele cu initiala
conditii.
Pentru
astfel de
sarcini
cu exceptia
iniţială
ecuație diferențială la un punct x0
trebuie specificate conditiile initiale, i.e.
valorile funcției y (x) și derivatele acesteia: y (x0) =
y0
y" (x0) = y"0 , . . . , y(n-1) (x0) = yn-10.

Formularea problemei
Al doilea tip de sarcini sunt așa-numitele
hotar, sau margine, în care
condiții suplimentare sunt date în formular
funcţional
rapoarte
între
solutiile dorite.
Al treilea tip de sarcini pentru obișnuit
ecuațiile diferențiale sunt probleme
propriile valori.

Formularea problemei
Să formulăm problema Cauchy.
Găsiți o soluție la diferența obișnuită
ecuația (ODE) de ordinul întâi, rezolvată
în raport cu derivata
y "f(x, y),
satisfacerea conditiei initiale
y (x0) y0

10.

Formularea problemei
Este necesar să găsiți pe segment astfel
functie continua
y = y(x), care
satisface ecuația diferențială
y " f (x, y) și condiția inițială y (x0) y0
acestea.
găsi
soluţie
diferenţial
ecuații. Găsirea unei astfel de soluții se numește
rezolvarea problemei Cauchy. Rezolvarea numerică a acesteia
sarcina este de a construi un tabel de aproximativ
valorile y1,y2,...,yn ale soluției ecuației y(x) în punctele
x1,x2,...,xn cu un pas h.
xi x0 i h,
i=1,2,...,n.

11.

Comun
ecuatii diferentiale
Ecuații în privat
derivate
Z Z
dy
0
2(y3)
2
2
X
y
dx
2
d y
2
2
t
1
2
z
z
dt
3 2 2 4
X
y
3
xdy=ydx
2
y'=x
2
11
2
18.01.2018

12.

Ecuații de ordinul întâi
dy
2(y3)
dx
Ecuații de ordinul doi
2
d y
t
1
2
dt
Z Z
0
2
2
X
y
2
3
xdy=ydx
Z Z
3 2 2 4
X y
2
2
y′=x
12
2
2
18.01.2018

13.

Exemplul 1. Pentru o ecuație diferențială
dy
2x
dx
y0 = 2 la x0 = 1
soluție generală: y = x2 +
CU
2 \u003d 1 + C, adică C \u003d 1
М0 (1; 2)
13
18.01.2018

14.

Starea Lipschitz
R[ a ,b ] (| x x0 | a, | y y0 | b)
f (x, y) f (x, y) N y y
14
18.01.2018

15.

Metode pentru rezolvarea aproximativă a diferenţialului
ecuații
Metode de analiză
Metode numerice
Metoda secventiala
aproximări – metodă
Picard
metoda lui Euler și
modificări
Metoda de integrare
diferenţial
ecuații folosind
serie de puteri
Metoda Runge-Kutta
metoda extrapolării
Adams
15
18.01.2018

16.

18.01.2018

17.

Rezolvați ecuația diferențială
y′=f(x, y) prin metoda numerică –
aceasta înseamnă pentru un dat
secvențe de argumente
x0, x1,…, xn și numerele y0,
fără a defini funcția y=F(x),
găsiți astfel de valori y1, y2, …, yn,
că yi=F(xi) și F(x0)=y0.
h=xk-xk-1
18.01.2018

18.

Fie ecuația diferențială
prima comanda
y'= f (x, y)
cu starea initiala
x=x0, y(x0)=y0
b a
h
n
etapa de integrare
18.01.2018

19.

19
18.01.2018

20.

xk 1
xk 1
f (x, y) y" dx y(x)
xk
xk 1
xk
y (xk 1) y (xk) yk 1 yk
xk
acesta este
yk 1 yk
xk 1
f (x, y)dx
xk
18.01.2018

21.

xk 1
f (x, y)dx f (x, y) x
k
k
xk 1
xk
f (xk , yk)(xk 1 xk) y " h
xk
yk 1 yk y "k h
yk 1 yk y "k h
Denota
da 1 da da
yk h y "k
da 1 da da
18.01.2018

22.

y
h
0
x0
x1
x2
X
18.01.2018

23.

Eroare de metodă
hM
n
y (xn) y n
(1 hN) 1
2N
Unde
f (x1 , y1) f (x1 , y2) N y1 y2
df
f
f
f
M
dx
X
y
18.01.2018

24.

Exemplul 1. Rezolvați y'=y-x cu inițială
condiția x0=0, y0=1,5 pe segmentul , h=0,25
Soluţie
i
(1)
0
1
2
3
4
5
6
xi
(2)
0
0.25
0.50
0.75
1.00
1.25
1.50
yi
(3)
1.5000
1.875
2.2812
2.7265
3.226
3.7758
4.4072
yi'=yi-xi
(4)
1.5000
1.6250
1.7812
1.9765
2.2206
2.5258
yi hy
"
i
(5)
0.3750
0.4062
0.4453
0.4941
0.5552
0.6314
18.01.2018

25.

metoda Euler
Introduceți x, y, h, b
Ieșire x, y
y: y hf x, y
x:x h
+
xb
Sfârşit
18.01.2018

26.

Metoda Euler îmbunătățită
yn+1 = yn + h/2
Să revenim la extinderea funcției într-o serie Taylor
o creştere a preciziei calculului se poate realiza prin menţinerea
membru care conține h2. y (t0) poate fi aproximat printr-o diferență finită:
Ținând cont de această expresie, extinderea funcției într-o serie Taylor ia forma
eroarea este de ordinul h3
18.01.2018

27.

18.01.2018

28.

Sarcină. Lasă diferența
ecuație de ordinul întâi
y'= f(x, y)
cu starea initiala
x=x0, y(x0)=y0
Găsiți o soluție la o ecuație pe un segment
yi 1 yi yi
18.01.2018

29.

k1 hf (x, y)
h
k1
k 2 hf (x, y)
2
2
h
k2
k3 hf (x, y)
2
2
k4 hf (x h, y k3)
18.01.2018

30.

1
y (k1 2k 2 2k3 k 4)
6
yi 1 yi yi
18.01.2018

31.

18.01.2018

32.

Eroare de metodă Rn(h5).
18.01.2018

33.

Exemplul 1. Rezolvați diferența
ecuația y′= y-x cu inițială
condiția x0=0, y(x0)=y0=1,5 prin metoda
Runge Kutta. Calculați cu o precizie de 0,01.
Soluţie
k1(0)=(y0-x0)h=1,5000*0,25=0,3750
k2(0)
k1(0)
h
x0 h (1,5000 0,1875) 0,125 0,25 0,3906
y0
2
2
18.01.2018

34.

k3(0)
k2(0)
h
x0 h (1,5000 0,1953) 0,125 0,25 0,3926
y0
2
2
k4(0)=[(y0+k3(0))-(x0+h)]h=[(1,5000+0,3926)0,125]*0,25=0,4106
1
y0 (0,3750 2 * 0,3906 2 * 0,3926 0,4106)
6
=0,3920
y1=1,50000+0,3920=1,8920
18.01.2018

35.

18.01.2018

36.

18.01.2018

37.

Metoda Runge-Kutta pentru rezolvarea sistemelor
ecuatii diferentiale
,
y "f (x, y, z)
z
"
g
X
,
y
,
z
18.01.2018

38.

1(i)
(i)
(i)
(i)
yi (k1 2k 2 2k3 k 4)
6
1(i)
(i)
(i)
(i)
zi (l1 2l2 2l3 l4)
6
, Unde
18.01.2018

39.

(i)
1
k
(i)
1
l
hf (xi, yi, zi)
hq(xi, yi, zi)
18.01.2018

40.

k
l
(i)
2
(i)
2
(i)
1
(i)
1
h
k
l
hf (xi, yi
,zi)
2
2
2
(i)
1
(i)
1
h
k
l
hq(xi, yi
,zi)
2
2
2
18.01.2018

41.

k
(i)
3
(i)
3
l
(i)
2
(i)
2
(i)
2
(i)
2
h
k
l
hf (xi, yi
,zi)
2
2
2
h
k
l
hq(xi, yi
,zi)
2
2
2
18.01.2018

42.

k
l
,
(i)
4
(i)
4
(i)
3
k
h
(i)
hf (xi, yi
, zi l3)
2
2
(i)
3
k
h
(i)
hq(xi, yi
, z i l3)
2
2
yi 1 yi yi
zi 1 zi zi
18.01.2018

43.

Metoda aproximărilor succesive
43
18.01.2018

44.

Prima abordare:
A doua aproximare:
A treia aproximare:
…
a n-a aproximare:
44
18.01.2018

45.

Teorema. Fie în vecinătatea punctului (x0; y0)
funcția f(x, y) este continuă și are
derivată parțială limitată f'y (x, y).
Apoi într-un interval care conține
punctul x0, secvența ( yi(x))
converge către funcția y(x) care servește
rezolvarea diferenţialului
ecuațiile y’ = f(x, y) și
satisfacerea condiţiei y(x0) = y0
45
18.01.2018

46.

Estimarea erorii metodei Picard
n 1
h
| y yn | NM
(n 1)!
n
unde M = max |f(x, y)|
N = max |f 'y(x, y)|
b
h min a,
M
46
18.01.2018

47. Metoda Picard a aproximărilor succesive

ecuație diferențială de ordinul al n-lea
Luați în considerare ecuația diferențială a primei
Ordin
y' = f(x, y)
(1)
cu conditiile initiale
y(x0) = y0
(2).
Se presupune că într-o vecinătate a punctului
M0(x0, y0) ecuația (1) satisface condițiile teoremei
existența și unicitatea soluției.

48.

Vom construi soluția dorită y = y(x) pentru valori
x x0 .
Cazul x x0 este similar.
Integrarea părților drepte și stângi ale ecuației (1) în
între x0 și x, obținem
X
y (x) y (x0) f (x, y)dx
x0
sau în virtutea condiţiei iniţiale (2), vom avea
X
y (x) y0 f (x, y)dx
x0
(3)

49.

Deoarece funcția dorită y = y(x) este sub
semn integral, atunci ecuația (3) este
integrală.
În mod evident, soluția ecuației integrale (3)
satisface ecuația diferențială (1) și
starea inițială (2).
Pentru a găsi această soluție, aplicăm metoda
aproximări succesive.
Inlocuind in egalitate (3) functia necunoscuta y
dată fiind valoarea y0, obținem prima aproximare
X
y1 y0 f (x, y0)dx
x0

50.

În plus, înlocuind în egalitate (3) în loc de necunoscut
funcția y găsită funcția y1, vom avea a doua
apropiere
X
y2 y0 f(x, y1)dx
etc.
x0
Toate aproximările ulterioare sunt construite conform formulei
X
yn y0 f (x, yn 1)dx
(n = 1, 2, …)
x0
Geometric
consecutiv
apropiere
sunt curbele yn = yn(x) (n = 1, 2, …),
trecând prin punctul comun M0(x0, y0).

51.

y
0
x0
x x+h
X
Cometariu.
La
metodă
succesiv
aproximații ca aproximarea inițială y0,
se poate alege orice funcție suficient de aproape de
solutie exacta y.
De exemplu, uneori este avantajos să luați ca y0
segmentul final al seriei Taylor al soluției dorite.

52.

Notă
Ce
la
utilizare
metodă
aproximări succesive, analiticitatea dreptului
o parte a ecuației diferențiale este opțională,
Prin urmare, această metodă poate fi utilizată în cazurile în care
Când
descompunere
solutii
diferenţial
Ecuațiile seriei de puteri sunt imposibile.
Exemplul 1. Prin metoda aproximărilor succesive
găsiți o soluție aproximativă a diferenţialului
ecuații
y' = x - y,
Satisfacerea condiției inițiale y(0) = 1.

53.

Soluţie. La fel de
se ia y0(x) = 1. Deoarece
elementar
apropiere
X
y 1 (x y)dx
0
atunci vom avea
X
x2
y1 1 (x 1)dx 1 x
2
0
În mod similar
3
x2
X
dx 1 x x 2
y2 1 x 1 x
2
6
0
X

54.

În același mod obținem
3
4
X
X
y3 1 x x 2
3 24
3
4
5
X
X
X
y4 1 x x 2
3 12 120
etc.

55. Sistem de ecuații diferențiale (metoda Picard)

Dat un sistem de ecuații diferențiale
dy
f(x, y)
dx
(4)
y(x0) y0
(5)
Unde
Scrierea ecuației vectoriale (4) în integrală
formă, vom avea

56.

X
y y0 f (x, y)dx
(6)
x0
unde sub integrala funcției vectoriale
vector înțeles
X
x0
X
f1 dx
x0
f dx
X
f n dx
x0
f1
f
f n

57.

aproximări succesive
sunt determinate de formula
X
y
(p)
y 0 f (x, y
(p1)
y (p) (p = 1, 2, …)
)dx
x0
Mai mult, de obicei se presupune
y(0)y
Această metodă este potrivită și pentru diferențial
Ecuația de ordinul n-a, dacă este scrisă sub forma
sisteme.

58.

Exemplul 2. Construiți mai multe consecutive
aproximări pentru rezolvarea sistemului
dy1
dx x y1 y2
dy2 x 2 y 2
1
dx
satisfacerea conditiilor initiale
y1(0) = 1; y2(0) = 0

59.

Soluţie. Avem:
X
y1 1 (x y1 y2)dx
0
X
y2 (x2 y12)dx
0
Prin urmare, presupunând
y1(0) = 1;
y2(0) = 0
primim
X
2
X
(1)
y1 1 (x 0)dx 1
2
0
X
3
X
(1)
y2 (x 2 1)dx x
3
0

60.

x2
x 3
x4 x6
1 x 1 x dx 1
2
3
24 36
0
X
(2)
1
y
4
5
2
X
X
x 1 x 2 dx x
4
20
0
X
y2
(2)
etc.

61.

Sfârșitul calculelor
n 1
h
| y yn | NM
(n 1)!
n
61
18.01.2018