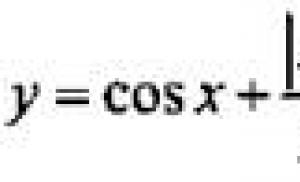Prezentare pe tema „semnificația geometrică a funcției derivate”. Sensul geometric al derivatului Sensul geometric al derivatului

Slide 2

Mai devreme sau mai târziu, fiecare idee matematică corectă își găsește aplicare într-un lucru sau altul. A.N. Krylov

Slide 3

Scopul lecției

1) aflați care este semnificația geometrică a derivatei, deduceți ecuații pentru tangenta la graficul funcției 2) Dezvoltați OUUN activității mentale: analiză, generalizare și sistematizare, gândire logică, percepția conștientă a materialului educațional 3) dezvoltați capacitatea de a-ți evalua nivelul de cunoștințe și dorința de a-l îmbunătăți, promovează dezvoltarea nevoii de autoeducare. Promovarea responsabilității și a colectivismului.

Slide 4

Vocabularul lecției

derivată, funcție liniară, coeficient unghiular, continuitate, tangente de unghiuri (acute, obtuz).

Slide 5

Faceți o pereche: fiecare elev lucrează independent timp de 3 minute, lucrează în perechi timp de 2 minute. Discutați rezultatele și notați răspunsurile pe cartonaș. (Cartonașul nr. 1 rămâne la elev pentru autocontrol, cardul nr. 2 trebuie predat profesorului)

Slide 6

Răspuns.

Faceți o pereche

Slide 7

Definiție

O funcție definită folosind formula y=khx+b se numește liniară. Numărul k=tg se numește panta dreptei.

Slide 8

y x -1 0 1 2 y=кх+b

Slide 9

y x -1 0 1 2 y=кх+b

Slide 10

y x 0 y=yₒ+к(х-xₒ)   x-xₒ y-yₒ xₒ x Mₒ(xₒ;yₒ) M(x;y) A(x;yₒ)

Slide 11

Ecuația unei drepte cu panta k care trece prin punctul (x0;y0) y=y0+k(x-x0) Ecuația unei drepte cu panta k care trece prin punctul (x0;y0) y=y0+k( x-x0) (1) Coeficientul unghiular al dreptei care trece prin punctele (x1;y1) și (x0;y0) (2)

Slide 12

y x -1 0 1 2 Aflați panta dreptei y=кх+b

Slide 13

Definiție

Tangenta la graficul funcției y=f(x) este poziția limită a secantei. desen

Slide 14

secanta tangentă

Slide 15

Lucrări practice de cercetare Sensul geometric al derivatului

Scop: Folosind datele din lucrările practice, determinați care este semnificația geometrică a derivatei.Echipament: rigle, raportoare, microcalculatoare, hârtie milimetrică cu un grafic trasat

Slide 16

Exercițiu

1. Construiți o tangentă la graficul funcției ... în punctul cu abscisă xₒ=2 2. Măsurați unghiul format de tangentă și direcția pozitivă a axei oX. 3. Scrieți =…. 4. Calculați tg=… folosind un microcalculator. 5. Calculați f´(xₒ), pentru a face acest lucru, găsiți f´(x) 6. Scrieți: f´(x)=…. ; f´(xₒ)=…. 7. Selectați două puncte pe graficul tangentei și notați coordonatele lor. 8. Calculați panta dreptei k folosind formula 9. Introduceți rezultatele calculului în tabel

Slide 17

Sensul geometric al derivatului

Valoarea derivatei funcției y=f(x) în punctul x0 este egală cu panta tangentei la graficul funcției y=f(x) în punctul (x0;f(x0))

Slide 18

Slide 19

Slide 20

Slide 21

Ecuația tangentei la graficul unei funcții

1. Scrieți ecuația unei drepte cu panta k care trece prin punctul 2. Înlocuiți k cu și y=y0+k(x-x0)

Pentru a vizualiza prezentarea cu imagini, design și diapozitive, descărcați fișierul și deschideți-l în PowerPoint pe calculatorul tau.
Conținutul text al slide-urilor prezentării: V.N. Egorova, profesor de matematică, KOU „Școala secundară nr. 1 (cu normă întreagă și cu frecvență redusă)” Definiția unei derivate. Derivatul unei funcții este unul dintre subiectele dificile din programa școlară. Nu fiecare absolvent va răspunde la întrebarea care este derivata AСВtg A-?tg B -?АВСLucrează oral Tangenta este raportul dintre latura opusă și latura adiacentă

АСВtg A-?tg В -?47АВСGăsiți măsura gradului< В.3Найдите градусную меру < А.Работа устноВычислите tgα, если α = 150°.

Figura prezintă grafice a trei funcții. Care crezi că crește mai repede? Lucru pe cale orală Kostya, Grisha și Matvey au primit un loc de muncă în același timp. Să vedem cum s-au schimbat veniturile lor în cursul anului: venitul lui Kostya s-a dublat în șase luni. Și venitul lui Grisha a crescut, dar doar puțin. Și venitul lui Matvey a scăzut la zero. Condițiile de pornire sunt aceleași, dar rata de schimbare a funcției este diferită. Cât despre Matvey, veniturile lui sunt în general negative. Lucrează oral

Intuitiv, estimăm cu ușurință rata de schimbare a unei funcții. Dar cum facem asta? Ceea ce ne uităm cu adevărat este cât de abrupt urcă (sau jos) graficul unei funcții. Cu alte cuvinte, cât de repede se schimbă y pe măsură ce x se schimbă? Evident, aceeași funcție în puncte diferite se poate schimba mai repede sau mai lent
Derivata este rata de schimbare a unei functii.
Probleme care duc la conceptul de derivat1. Problemă cu privire la viteza de schimbare a unei funcții S-a trasat graficul unei anumite funcții. Să luăm o abscisă pe ea. Să desenăm o tangentă la graficul funcției în acest punct. Pentru a estima abruptul graficului unei funcții, o valoare convenabilă este tangenta unghiului tangentei. Ca unghi de înclinare, luăm unghiul dintre tangentă și direcția pozitivă a axei OX Să aflăm k=tg α∆AMN: ˂ ANM = 90˚, tgα = 𝐴𝑁𝑀𝑁 Semnificația geometrică a derivatei Rezumat

Derivata unei functii intr-un punct este egala cu panta tangentei trasate la graficul functiei in acel punct. Semnificația geometrică a derivatei Derivata unei funcții este egală cu tangentei unghiului tangentei - acesta este semnificația geometrică a derivatei
STTimpul de călătorie este egal cu tABU=S / tProbleme care duc la conceptul de derivat2. Problema cu viteza
SARCINĂ. Un corp (punct material) se deplasează de-a lungul unei linii drepte pe care sunt date originea, unitatea de măsură (metrul) și direcția. Legea mișcării este dată de formula S=s(t), unde t este timpul (în secunde), s(t) este poziția corpului pe o dreaptă (coordonata unui punct material în mișcare) în timp t relativ la origine (în metri). Aflați viteza corpului la momentul t (în m/s).SOLUȚIE. Să presupunem că la momentul t corpul se afla în punctul MOM=S(t). Să dăm argumentului t un increment ∆t și să considerăm situația în momentul de timp t + ∆t. Coordonata punctului material va deveni diferită, corpul în acest moment va fi în punctul P: OP= s(t+ ∆t) – s(t). Aceasta înseamnă că în ∆t secunde corpul s-a deplasat din punctul M în punctul P. Avem: MP=OP – OM = s(t+ ∆t) – s(t). Diferența rezultată se numește increment al funcției: s(t+ ∆t) – s(t)= ∆s. Deci, MP= ∆s (m), apoi viteza medie pe perioada de timp: 𝑣av.=∆𝑆∆𝑡 Viteza medie S(t)S(t + Δt)0МРΔt
Derivata functiei y = f(x) la un punct dat x0 este limita raportului dintre incrementul functiei in acest punct si incrementul argumentului, cu conditia ca incrementul argumentului sa tina la zero. denumire: 𝑦′𝑥0 sau 𝑓′𝑥0 𝑓′𝑥0=lim∆ 𝑥→0∆𝑦∆𝑥 sau 𝑓′𝑥0=lim∆𝑥→0∆𝑥∆𝑥∆S Definiție
Viteza instantanee este viteza medie pe interval, cu condiția ca ∆t→0, adică: 𝒍𝒊𝒎∆𝒕→𝟎𝒗av.=𝒍𝒊𝒎∆𝒕→𝟎∆𝑺∆∆𝑺∆∆𝑺∆∆𝑺∆𝒕 Fie ca argumentul x∆𝒕 să considerăm două valori instantanee ale vitezei instantanee. unde ∆x este incrementul argumentului Să aflăm incrementul funcției ∆f(x) = f(x0 + ∆x) – f(x0) Să găsim raportul dintre incrementul funcției și incrementul argument ∆𝐟(x)∆x Să calculăm limita acestui raport la ∆x → 0 lim∆𝑥→0Δ𝑓(𝑥)Δ𝑥=𝑓′(𝑥) Algoritm pentru găsirea derivatei (prin definiție) Soluție de calcul a derivatei Note

Exemplul 2. Aflați derivata funcției y = x Rezolvare: f(x) = x.1. Luați două valori ale argumentului x și x + Δx.2.∆𝑓=𝑓𝑥+∆𝑥−𝑓𝑥=𝑥 +∆𝑥−𝑥=∆𝑥 .3.∆𝑓∆𝑥=∆𝑥∆𝑥=1,4.𝑓′𝑥=lim∆𝑥→0∆𝑓∆𝑥=lim.∆𝑥=lim. ′ = 1 Exemplu de calcul al derivatei Exemplul 3 .Aflați derivata funcției y = x2Soluție: f(x) = x2.1.Se iau două valori ale argumentului x și x + Δx.2.∆𝑓=𝑓𝑥 +∆𝑥−𝑓𝑥=(𝑥+∆𝑥)2−𝑥2=𝑥2 +2𝑥∆𝑥+(∆𝑥) 2–𝑥2 = ∆𝑥 (2𝑥+∆.𝑥)∆.𝑥+∆.𝑥)∆. ∆𝑥 ( 2𝑥+∆𝑥) ∆𝑥 = 2𝑥+∆𝑥.4. 𝑓′𝑥=lim∆𝑥→0∆𝑓∆𝑥=lim∆𝑥→0(2𝑓′𝑥=lim∆𝑥→0∆𝑓∆𝑥=lim∆𝑥→0(2𝑥→0(2𝑥→0)𝑥→0+∆=lim∆+❑ ∆𝑥 →0∆𝑥=2𝑥.Deci, (𝒙 𝟐)′ = 2x Exemplu de calcul a derivatei Exemplul 4. Aflați derivata funcției y =𝒌𝒙+𝒎Rezolvare: f(x) = 𝑘𝑥+𝑚 s.1. ​​al argumentului x și x + Δx.2.∆𝑓=𝑓𝑥+∆𝑥−𝑓𝑥=𝑘𝑥+ ∆𝑥+𝑚− 𝑘𝑥−𝑚=𝑘𝑥−𝑚=𝑘𝑘−𝑘𝑥−𝑘𝑥=𝑘𝑥+ ∆𝑥.3.∆𝑓 (𝑥)∆𝑥=𝑘∆𝑥∆𝑥=𝑘.4. 𝑓′𝑥=lim∆𝑥→0 ∆𝑓∆𝑥=lim∆𝑥→0𝑘. calcularea derivatei Exemplul 5. Aflați derivata funcției y = 𝟏𝒙Rezolvare: f(x) = 1𝑥.1.Se iau două valori ale argumentului x și x + Δx.2.∆𝑓=𝑓𝑥+∆𝑥−𝑓𝑥−𝑓𝑥−𝑓 = 1𝑥+∆𝑥−1𝑥=𝑥−𝑥−∆𝑥𝑥(𝑥+∆𝑥)=−∆𝑥𝑥(𝑥+∆ 𝑥).3.∆ 𝑥𝑥)∆=𝑥)𝑥) 𝑥+∆𝑥) :∆𝑥=−∆𝑥𝑥(𝑥+∆𝑥)∆𝑥=−1𝑥(𝑥+∆𝑥) .4.𝑓′𝑥 =lim∆𝑥 →0∆𝑥∆𝑥∆𝑥=∆∆𝑥 𝑥 +∆𝑥)=−1lim∆𝑥→01𝑥2+𝑥∆𝑥=−lim∆𝑥→01lim∆𝑥→0𝑥2+lim∆ 𝑥→0𝑥∆𝑥 = - 𝑥∆𝑥 = - 𝑥∆𝑥 = - 𝒙 fraza noastră a fost dedicată 𝟐𝑏 azi... In timpul lectiei am invatat ca... In lectia pe care am invatat-o... Derivata unei functii intr-un punct este egala cu... tangenta trasata la graficul functiei intr-un punct dat.Rata de modificare a o funcție este... Mi-a fost greu... BINE FĂCUT!
ppt_y

Fișiere atașate

Instituție de învățământ bugetar municipal

Școala secundară Glukhovskaya

Rezumatul unei lecții deschise de algebră

pe tema:

„Derivatul și sensul său geometric. Derivată în examenul de stat unificat”

profesor de matematică și informatică

Dikalov Dmitri Ghenadievici

2015

Rezumatul lecției pe tema: Derivată și semnificația sa geometrică

Obiectivele lecției:

Educational:

• Examinați conceptele de bază ale secțiunii „Derivată”
• Învățați studenții cum să rezolve rapid problemele pe tema „Derivată” din opțiunile pentru examenul de stat unificat

Educational:

• Dezvoltarea interesului cognitiv, gândirea logică, dezvoltarea memoriei, atenția.
• cultivarea interesului pentru structura rețelelor de calculatoare.

Educational:

• cultivați o atitudine conștiincioasă față de muncă și inițiativă;
• insuflarea disciplinei si organizarii

Tip de lecție:

• lectie de repetare si consolidare a cunostintelor

Structura lecției:

• Organizarea timpului;
• actualizarea cunoștințelor de bază
• rezolvarea problemelor
• teme pentru acasă

Echipamente : program de prezentare Microsoft Office PowerPoint, prezentare, calculator, proiector multimedia, tabla interactiva.

Planul lecției:

1. Moment organizatoric (1 min.)
2. Actualizarea cunoștințelor (5 min)
3. Rezolvarea problemelor (34 min)
4. Rezumatul lecției (4 min)
5. Tema pentru acasă (1 min.)

În timpul orelor:

I. Moment organizatoric

Profesorul salută, prezintă tema, obiectivele și progresul lecției.

II. Actualizarea cunoștințelor

1. 1. Care este semnificația geometrică a derivatei?
2. Cum se găsesc intervalele funcțiilor crescătoare (descrescătoare)?
3. Care este algoritmul pentru găsirea punctelor extreme?
4. Cum diferă punctele staționare de punctele extreme?

III. Rezolvarea problemelor.

Rezolvarea problemelor privind găsirea derivatei într-un punct, găsirea intervalelor de creștere și descreștere, găsirea punctelor la care derivata = 0, găsirea celor mai mari și mai mici valori ale unei funcții.

Elevii rezolvă aceste probleme folosind o tablă interactivă; fiecare problemă este descrisă pe un diapozitiv separat.

Elevii discută nuanțele rezolvării problemelor pe măsură ce se deplasează prin diapozitive.

Următoarele probleme sunt oferite elevilor pentru a le rezolva în mod independent.

IV. Rezumând lecția.

Pentru a rezuma lecția, 1-2 elevi sunt chemați la tablă pentru a rezolva probleme din manualul nr. 956 (1,2): găsiți intervalele funcției crescătoare și descrescătoare y = 2x 3 +3x 2 -2

Soluția studentului:

Pentru a afla intervalele de creștere și scădere ale unei funcții, găsim derivata acesteia:

y`=6x 2 +6x

Pentru a găsi puncte staționare, echivalăm derivata cu 0 și rezolvăm această ecuație, obținem punctele x=0 și x=-1. Să găsim punctele extreme dintre aceste puncte. Pentru a face acest lucru, determinăm semnul derivatei pe fiecare dintre cele trei intervale. Pe intervalul x0, derivata este pozitivă, ceea ce înseamnă că la aceste intervale funcția crește. Pe interval

1

Elevul notează răspunsul.

V. Tema pentru acasă

Nr. 957, Nr. 956 (de completat)

Acordarea de note elevilor care au fost activi la lecție.

„Formulele trigonometrice” - Cos x. Cos. Formule pentru transformarea unei sume într-un produs.Sin (x+y). Formule cu argument dublu. Formule de conversie prod. în sumă. Formule de adunare. Trigonometrie. Tg. Sin x. Raport între f-s. F-ly jumătate de argument. Ecuații trigonometrice.

„Calculul ariei unui trapez curbiliniu” - Arii trapezelor curbilinie. Formule pentru calcularea suprafeței. Ce fel de figură se numește trapez curbat? Repetarea teoriei. Aria unui trapez curbat. Găsiți antiderivată a funcției. Care dintre figuri sunt trapeze curbilinii. Soluţie. Șabloane de grafice de funcție. Pregătirea pentru examene. O figură care nu este un trapez curbat.

„Determină dacă o funcție este pară sau impară” - Funcții impare. nu este chiar. Funcţie. Graficul unei funcții impare. Funcția este egală? Coloană. Graficul unei funcții pare. Chiar și funcții. Funcția este ciudată. Simetrie în jurul axei. Exemplu. Funcția este ciudată? Nu este ciudat. Funcții pare și impare.

„Logaritmii și proprietățile lor” - Proprietăți ale gradelor. Tabelele logaritmice. Proprietățile logaritmilor. Istoria logaritmilor. Revizuiți definiția logaritmului. Calculati. Aplicarea materialului studiat. Verifică. Definiţia logarithm. Descoperirea logaritmilor. Găsiți a doua jumătate a formulei.

„“Inegalități logaritmice” clasa a XI-a” - Aplicarea teoremei. log26 … log210 log0,36 … log0,310. Definiție. > ,T.K. 6<10 и функция у=log0,3x - убывающая. Повторить свойства логарифмической функции. График какой функции изображен на рисунке? Сравните числа: Логарифмические неравенства. < , Т.К. 6<10 и функция у=log2x - возрастающая. Найдите область определения функции: Если а>1, atunci logа f(x)>logа g(x)? Daca 0<а<1, то logа f(x)>loga g(x) ?.

„Multe antiderivate” - Antiderivat. Alegeți un antiderivat pentru funcții. Determinarea nivelului de cunoștințe. Rezolvarea unui nou tip de sarcină. Sondaj frontal. Verificarea progresului. Controlul ieșirii. Munca educațională independentă. Conceptul de integrare. Vedere generală a primitivilor. Formule. Sistem de evaluare.