Acasă » clasa a 9-a » Fractalii din lumea reală sunt un obiect de studiu. Laboratorul de Cercetare Spațială. luarea în considerare a suprafețelor complexe ale membranelor celulare

Fractalii din lumea reală sunt un obiect de studiu. Laboratorul de Cercetare Spațială. luarea în considerare a suprafețelor complexe ale membranelor celulare

Martynov Daniil

Manager de proiect:

Martynova Lyudmila Iurievna

Instituţie:

Instituția de învățământ municipală „Școala secundară Kriushinskaya”

În curs lucrări de cercetare în matematică „Fractali din jurul nostru” Un elev de clasa a VIII-a și-a stabilit un obiectiv să arate că matematica nu este o materie fără suflet, ea poate exprima lumea spirituală a omului și a societății prin crearea propriului fractal geometric " Stea».

Într-o lucrare de cercetare privind matematica „Fractali în jurul nostru”, autorul construiește un fractal geometric „Steaua” ca parte a proiectului și oferă recomandări privind aplicarea practică a fractalului creat, încearcă să găsească o legătură între fractali și triunghiurile lui Pascal în proces de cercetare matematică.

În propus proiect de matematică „Fractali din jurul nostru” autorul ajunge la concluzia că noile idei ale geometriei fractale vor ajuta la studierea multor fenomene misterioase ale naturii înconjurătoare. Procesarea imaginilor și metodele de recunoaștere a modelelor care folosesc concepte noi permit cercetătorilor să folosească acest aparat matematic pentru a descrie cantitativ un număr mare de obiecte și structuri naturale.

Introducere
1. Justificarea și construcția fractalului geometric „Steaua”.
2. Găsirea legăturii dintre fractali și triunghiurile lui Pascal.
3. Recomandări pentru aplicarea practică a fractalului creat.
Concluzie

Introducere

Mulți dintre colegii mei cred că matematica este o știință exactă și plictisitoare, probleme, ecuații, grafice, formule... Ce ar putea fi interesant aici? Geometria secolului XXI. Rece, dificil, deloc interesant...

„De ce se numește așa? Unul dintre motive este că nu poate descrie forma unui nor, a unui munte, a unui copac sau a unui țărm. Norii nu sunt sfere, munții nu sunt conuri, țărmurile nu sunt cercuri, iar scoarța nu este. netedă, iar fulgerul nu se extinde în linie dreaptă. Natura ne arată nu doar un grad mai înalt, ci un cu totul alt nivel de complexitate” Benoit Mandelbrot.

Cu munca mea de cercetare am încercat să infirm cele de mai sus. Acest lucru a devenit posibil după descoperirea fractalilor - figuri auto-similare care au o serie de proprietăți interesante, care au făcut posibilă compararea fractalilor cu obiecte naturale.

Ipoteză – « Tot ceea ce există în lumea reală este un fractal».

Ţintă - arată că matematica nu este un subiect fără suflet, ea poate exprima lumea spirituală a omului și a societății prin crearea propriului fractal geometric " Stea».

Obiect de studiu - fractali în matematică și în lumea reală.

Analizați și revizuiți literatura de specialitate pe tema de cercetare.
Luați în considerare și studiați diferite tipuri de fractali.
Stabiliți relația dintre triunghiul lui Pascal și operele literare.
Inventează și creează-ți propriul fractal, creează un program pentru construirea unei imagini grafice a unui fractal geometric " Stea».
Luați în considerare posibilitățile de aplicare practică a fractalului creat.

Relevanţă se determină subiectul declarat, în primul rând, subiect cercetare, care este geometria fractală.

Structura muncii de cercetare include o introducere, două capitole, o concluzie, o listă de referințe și anexe.

În introducere se fundamentează relevanța și noutatea temei de cercetare, se definesc problema, subiectul, scopul, sarcinile, etapele de lucru, semnificația teoretică și practică a lucrării.

În primul capitol Este dezvăluită problema istoriei apariției conceptului de fractal, clasificarea fractalilor și utilizarea fractalilor.

În al doilea capitol Este investigat și dovedit că figura geometrică pe care am creat-o " Stea„Este un fractal, prin modificarea parametrilor fractalului creat, am primit o întreagă galerie de ornamente frumoase care pot fi folosite pentru aplicații practice: în producția de țesături, materiale de finisare și în valorologie.

Instituție de învățământ bugetar municipal

„Școala secundară Siverskaya nr. 3”

Cercetare

matematică.

Am făcut treaba

elev de clasa a VIII-a-1

Emelin Pavel

Director stiintific

profesor de matematică

Tupitsyna Natalya Alekseevna

Satul Siversky

anul 2014

Matematica este impregnată de frumusețe și armonie,

Trebuie doar să vezi această frumusețe.

B. Mandelbrot

Introducere_________________________________________3-4pp.

Capitolul 1.istoria apariției fractalilor._______5-6pp.

Capitolul 2. Clasificarea fractalilor.______6-10pp.

Fractali geometrici

Fractali algebrici

Fractali stocastici

Capitolul 3. „Geometria fractală a naturii”______11-13pp.

Capitolul 4. Aplicarea fractalilor_______________13-15pp.

Capitolul 5 Lucrări practice__________________16-24pp.

Concluzie_________________________________25.pag

Listă de referințe și resurse de internet________26 pagini.

Introducere

Matematică,

daca te uiti corect,

reflectă nu numai adevărul,

dar şi o frumuseţe incomparabilă.

Bertrand Russell

Cuvântul „fractal” este ceva despre care mulți oameni vorbesc în aceste zile, de la oameni de știință până la liceeni. Apare pe coperțile multor manuale de matematică, reviste de știință și cutii de software de calculator. Imaginile color ale fractalilor pot fi găsite peste tot astăzi: de la cărți poștale, tricouri până la imagini de pe desktopul unui computer personal. Deci, care sunt aceste forme colorate pe care le vedem în jur?

Matematica este cea mai veche știință. Majoritatea oamenilor credeau că geometria în natură se limitează la figuri simple precum linia, cercul, poligonul, sfera etc. După cum se dovedește, multe sisteme naturale sunt atât de complexe încât utilizarea doar a obiectelor familiare de geometrie obișnuită pentru a le modela pare fără speranță. Cum, de exemplu, puteți construi un model al unui lanț muntos sau al unei coroane de copac din punct de vedere geometrie? Cum să descriem diversitatea diversității biologice pe care o observăm în lumea plantelor și animalelor? Cum să ne imaginăm complexitatea sistemului circulator, constând din multe capilare și vase și care furnizează sânge în fiecare celulă a corpului uman? Imaginați-vă structura plămânilor și rinichilor, care amintește în structura arborilor cu o coroană ramificată?

Fractalii sunt instrumente potrivite pentru a explora aceste întrebări. Adesea ceea ce vedem în natură ne intrigă cu repetarea nesfârșită a aceluiași tipar, crescut sau micșorat de câteva ori. De exemplu, un copac are ramuri. Pe aceste ramuri sunt ramuri mai mici etc. Teoretic, elementul de ramificare se repetă la infinit, devenind din ce în ce mai mic. Același lucru poate fi văzut atunci când priviți o fotografie a terenului muntos. Încercați să măriți puțin mai aproape de lanțul muntos --- veți vedea din nou munții. Așa se manifestă proprietatea auto-asemănării caracteristică fractalilor.

Studiul fractalilor deschide posibilități minunate, atât în studiul unui număr infinit de aplicații, cât și în domeniul matematicii. Aplicațiile fractalilor sunt foarte extinse! Până la urmă, aceste obiecte sunt atât de frumoase încât sunt folosite de designeri, artiști, cu ajutorul lor sunt desenate în grafică multe elemente: copaci, nori, munți etc. Dar fractalii sunt folosiți chiar și ca antene în multe telefoane mobile.

Pentru mulți haologi (oameni de știință care studiază fractalii și haosul) acesta nu este doar un nou domeniu de cunoaștere care combină matematica, fizica teoretică, arta și tehnologia computerelor - este o revoluție. Aceasta este descoperirea unui nou tip de geometrie, geometria care descrie lumea din jurul nostru și care poate fi văzută nu numai în manuale, ci și în natură și peste tot în universul nemărginit..

În munca mea, am decis să „ating” lumea frumuseții și m-am hotărât pentru mine...

Scopul lucrării: crearea de obiecte ale căror imagini sunt foarte asemănătoare cu cele naturale.

Metode de cercetare: analiză comparativă, sinteză, modelare.

Sarcini:

cunoașterea conceptului, istoria originii și cercetările lui B. Mandelbrot,

G. Koch, V. Sierpinsky și alții;

cunoașterea diferitelor tipuri de mulțimi fractale;

studierea literaturii științifice populare pe această problemă, familiarizarea cu

ipoteze științifice;

găsirea confirmării teoriei fractalității lumii înconjurătoare;

studierea utilizării fractalilor în alte științe și în practică;

efectuarea unui experiment pentru a crea propriile imagini fractale.

Întrebarea fundamentală a lucrării:

Pentru a arăta că matematica nu este un subiect sec, fără suflet; ea poate exprima lumea spirituală a unei persoane în mod individual și în societate în ansamblu.

Subiect de studiu: Geometrie fractală.

Obiect de studiu: fractali în matematică și în lumea reală.

Ipoteză: Tot ceea ce există în lumea reală este un fractal.

Metode de cercetare: analitic, căutare.

Relevanţă Tema enunțată este determinată, în primul rând, de subiectul cercetării, care este geometria fractală.

Rezultate asteptate: Pe parcursul activității, voi putea să-mi extind cunoștințele în domeniul matematicii, să văd frumusețea geometriei fractale și să încep să lucrez la crearea propriilor fractali.

Rezultatul muncii va fi crearea unei prezentări pe computer, a unui buletin informativ și a unei broșuri.

Capitolul 1. Istorie

Benoit Mandelbrot

Conceptul de „fractal” a fost inventat de Benoit Mandelbrot. Cuvântul provine din latinescul „fractus”, care înseamnă „rupt, rupt”.

Fractal (lat. fractus - zdrobit, spart, spart) este un termen care înseamnă o figură geometrică complexă care are proprietatea auto-asemănării, adică compusă din mai multe părți, fiecare dintre ele similară întregii figuri.

Obiectele matematice la care se referă se caracterizează prin proprietăți extrem de interesante. În geometria obișnuită, o linie are o dimensiune, o suprafață are două dimensiuni și o figură spațială are trei dimensiuni. Fractalii nu sunt linii sau suprafețe, ci, dacă vă puteți imagina, ceva între ele. Pe măsură ce dimensiunea crește, și volumul fractalului crește, dar dimensiunea (exponentul) acestuia nu este un întreg, ci o valoare fracțională și, prin urmare, limita figurii fractale nu este o linie: la o mărire mare devine clar că aceasta este neclară și constă din spirale și bucle, repetându-se la scara de mărire mică a figurii în sine. Această regularitate geometrică se numește invarianță la scară sau auto-similaritate. Aceasta este ceea ce determină dimensiunea fracțională a figurilor fractale.

Înainte de apariția geometriei fractale, știința s-a ocupat de sisteme conținute în trei dimensiuni spațiale. Datorită lui Einstein, a devenit clar că spațiul tridimensional este doar un model al realității, și nu realitatea în sine. De fapt, lumea noastră este situată într-un continuum spațiu-timp cu patru dimensiuni.
Datorită lui Mandelbrot, a devenit clar cum arată spațiul cu patru dimensiuni, la figurat vorbind, fața fractală a Haosului. Benoit Mandelbrot a descoperit că a patra dimensiune include nu numai primele trei dimensiuni, ci și (acest lucru este foarte important!) intervalele dintre ele.

Geometria recursivă (sau fractală) înlocuiește geometria euclidiană. Noua știință este capabilă să descrie adevărata natură a corpurilor și a fenomenelor. Geometria euclidiană s-a ocupat doar de obiecte artificiale, imaginare, aparținând trei dimensiuni. Doar a patra dimensiune le poate transforma în realitate.

Lichid, gaz, solid - trei stări fizice familiare ale materiei existente în lumea tridimensională. Dar care este dimensiunea unui nor de fum, a unui nor sau, mai exact, a granițelor lor, erodate continuu de mișcarea turbulentă a aerului?

Practic, fractalii sunt clasificați în trei grupe:

Fractali algebrici

Fractali stocastici

Fractali geometrici

Să aruncăm o privire mai atentă la fiecare dintre ele.

Capitolul 2. Clasificarea fractalilor

Fractali geometrici

Benoit Mandelbrot a propus un model fractal, care a devenit deja un clasic și este adesea folosit pentru a demonstra atât un exemplu tipic de fractal în sine, cât și pentru a demonstra frumusețea fractalilor, care atrage, de asemenea, cercetători, artiști și pur și simplu oameni interesați.

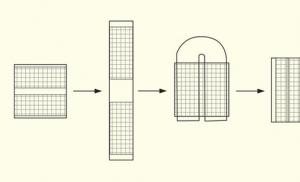
Aici a început istoria fractalilor. Acest tip de fractal se obține prin construcții geometrice simple. De obicei, atunci când construiesc acești fractali, ei fac acest lucru: iau o „sămânță” - o axiomă - un set de segmente pe baza cărora va fi construit fractalul. În continuare, acestei „sămânțe” i se aplică un set de reguli, care o transformă într-un fel de figură geometrică. Apoi, același set de reguli este aplicat din nou pentru fiecare parte a acestei figuri. Cu fiecare pas, figura va deveni din ce în ce mai complexă, iar dacă realizăm (cel puțin în mintea noastră) un număr infinit de transformări, vom obține un fractal geometric.

Fractalii din această clasă sunt cei mai vizuali, deoarece auto-asemănarea este imediat vizibilă în ei la orice scară de observație. În cazul bidimensional, astfel de fractali pot fi obținuți prin specificarea unei linii întrerupte numită generator. Într-un pas al algoritmului, fiecare dintre segmentele care alcătuiesc polilinia este înlocuit cu o polilinie generatoare, la scara corespunzătoare. Ca rezultat al repetarii nesfârșite a acestei proceduri (sau, mai precis, când mergeți la limită), se obține o curbă fractală. În ciuda complexității aparente a curbei rezultate, aspectul său general este determinat doar de forma generatorului. Exemple de astfel de curbe sunt: curba Koch (Fig. 7), curba Peano (Fig. 8), curba Minkowski.

La începutul secolului al XX-lea, matematicienii căutau curbe care să nu aibă în niciun punct o tangentă. Aceasta însemna că curba și-a schimbat brusc direcția și cu o viteză enorm de mare (derivata era egală cu infinitul). Căutarea acestor curbe nu a fost cauzată doar de interesul inactiv al matematicienilor. Cert este că la începutul secolului al XX-lea mecanica cuantică s-a dezvoltat foarte rapid. Cercetătorul M. Brown a schițat traiectoria de mișcare a particulelor în suspensie în apă și a explicat acest fenomen după cum urmează: atomii în mișcare aleatoriu ai lichidului lovesc particulele suspendate și, prin urmare, le pun în mișcare. După această explicație a mișcării browniene, oamenii de știință s-au confruntat cu sarcina de a găsi o curbă care să arate cel mai bine mișcarea particulelor browniene. Pentru a face acest lucru, curba trebuia să îndeplinească următoarele proprietăți: să nu aibă tangentă în niciun punct. Matematicianul Koch a propus o astfel de curbă.

Curba Koch este un fractal geometric tipic. Procesul de construire este următorul: luăm un singur segment, îl împărțim în trei părți egale și înlocuim intervalul din mijloc cu un triunghi echilateral fără acest segment. Ca rezultat, se formează o linie întreruptă, constând din patru verigi cu lungimea de 1/3. În pasul următor, repetăm operația pentru fiecare dintre cele patru legături rezultate etc...

Curba limită este curba Koch.

Fulgul de nea Koch. Efectuând o transformare similară pe laturile unui triunghi echilateral, puteți obține o imagine fractală a unui fulg de zăpadă Koch.

De asemenea, un alt reprezentant simplu al unui fractal geometric este Piața Sierpinski. Este construit destul de simplu: pătratul este împărțit prin linii drepte paralele cu laturile sale în 9 pătrate egale. Pătratul central este eliminat din pătrat. Rezultatul este un set format din cele 8 pătrate rămase de „primul rang”. Făcând exact același lucru cu fiecare dintre pătratele de rangul întâi, obținem un set format din 64 de pătrate de rangul doi. Continuând acest proces la nesfârșit, obținem o succesiune infinită sau pătrat Sierpinski.

Fractali algebrici

Acesta este cel mai mare grup de fractali. Fractalii algebrici își primesc numele deoarece sunt construiți folosind formule algebrice simple.

Ele sunt obținute folosind procese neliniare în n-spații dimensionale. Se știe că sistemele dinamice neliniare au mai multe stări stabile. Starea în care se află sistemul dinamic după un anumit număr de iterații depinde de starea sa inițială. Prin urmare, fiecare stare stabilă (sau, după cum se spune, atractor) are o anumită regiune de stări inițiale, din care sistemul va cădea în mod necesar în stările finale luate în considerare. Astfel, spațiul de fază al sistemului este împărțit în zone de atractie atractori. Dacă spațiul de fază este bidimensional, atunci prin colorarea zonelor de atracție cu culori diferite, se poate obține portret faza de culoare acest sistem (proces iterativ). Schimbând algoritmul de selecție a culorii, puteți obține modele fractale complexe cu modele multicolore bizare. Ceea ce a fost o surpriză pentru matematicieni a fost capacitatea de a genera structuri foarte complexe folosind algoritmi primitivi.

Ca exemplu, luați în considerare mulțimea Mandelbrot. Ei îl construiesc folosind numere complexe.

O secțiune a graniței mulțimii Mandelbrot, mărită de 200 de ori.

Setul Mandelbrot contine puncte care, in timpulinfinit numărul de iterații nu ajunge la infinit (punctele care sunt negre). Puncte aparținând graniței mulțimii(aici apar structurile complexe) merg la infinit într-un număr finit de iterații, iar punctele aflate în afara mulțimii ajung la infinit după mai multe iterații (fond alb).

Un exemplu de alt fractal algebric este mulțimea Julia. Există 2 varietăți ale acestui fractal.În mod surprinzător, mulțimile Julia sunt formate folosind aceeași formulă ca și mulțimea Mandelbrot. Setul Julia a fost inventat de matematicianul francez Gaston Julia, după care a fost numit setul.

Fapt interesant, unii fractali algebrici seamănă izbitor cu imagini de animale, plante și alte obiecte biologice, drept urmare sunt numiți biomorfi.

Fractali stocastici

O altă clasă binecunoscută de fractali sunt fractalii stocastici, care se obțin dacă unii dintre parametrii săi sunt modificați aleatoriu într-un proces iterativ. În acest caz, obiectele rezultate sunt foarte asemănătoare cu cele naturale - copaci asimetrici, coaste accidentate etc.

Un reprezentant tipic al acestui grup de fractali este „plasma”.

Pentru a-l construi, se ia un dreptunghi și se determină o culoare pentru fiecare dintre colțurile sale. Apoi, punctul central al dreptunghiului este găsit și pictat cu o culoare egală cu media aritmetică a culorilor de la colțurile dreptunghiului plus un număr aleatoriu. Cu cât numărul aleatoriu este mai mare, cu atât desenul va fi mai „zdrențuit”. Dacă presupunem că culoarea punctului este înălțimea deasupra nivelului mării, obținem un lanț muntos în loc de plasmă. Pe acest principiu, munții sunt modelați în majoritatea programelor. Folosind un algoritm similar cu plasma, se construiește o hartă a înălțimii, i se aplică diverse filtre, se aplică o textură și munții fotorealistici sunt pregătiți

Dacă ne uităm la acest fractal în secțiune transversală, vom vedea că acest fractal este tridimensional și are o „rugozitate”, tocmai din cauza acestei „rugozi” există o aplicație foarte importantă a acestui fractal.

Să presupunem că trebuie să descrii forma unui munte. Figurile obișnuite din geometria euclidiană nu vor ajuta aici, deoarece nu țin cont de topografia suprafeței. Dar atunci când combinați geometria convențională cu geometria fractală, puteți obține chiar „asperitatea” unui munte. Trebuie să aplicăm plasmă pe un con obișnuit și vom obține relieful unui munte. Astfel de operații pot fi efectuate cu multe alte obiecte din natură; datorită fractalilor stocastici, natura însăși poate fi descrisă.

Acum să vorbim despre fractali geometrici.

Capitolul 3 „Geometria fractală a naturii”

" De ce geometria este adesea numită „rece” și „uscă”? Un motiv este că nu poate descrie forma unui nor, munte, coastă sau copac. Norii nu sunt sfere, munții nu sunt conuri, coastele nu sunt cercuri, scoarță de copac nu este netedă, fulgerul nu călătorește în linie dreaptă. Mai general, susțin că multe obiecte din Natură sunt atât de neregulate și fragmentate încât, în comparație cu Euclid - un termen care în această lucrare înseamnă toată geometria standard - Natura nu are doar o complexitate mai mare. , dar complexitatea la un nivel complet diferit. Numărul de scări de lungimi diferite ale obiectelor naturale este, pentru toate scopurile practice, infinit."

(Benoit Mandelbrot „Geometria fractală a naturii” ).

Frumusețea fractalilor este dublă: încântă ochiul, așa cum demonstrează expoziția mondială de imagini fractale, organizată de un grup de matematicieni din Bremen sub conducerea lui Peitgen și Richter. Mai târziu, exponatele acestei expoziții grandioase au fost surprinse în ilustrații pentru cartea acelorași autori, „Frumusețea fractalilor”. Dar există un alt aspect, mai abstract sau mai sublim, al frumuseții fractalilor, deschis, după R. Feynman, doar privirii mentale a unui teoretician, în acest sens, fractalii sunt frumoși datorită frumuseții unei probleme matematice dificile. . Benoit Mandelbrot le-a subliniat contemporanilor săi (și, probabil, descendenților săi) un decalaj enervant în Elementele lui Euclid, prin care, fără a observa omisiunea, aproape două milenii de umanitate a înțeles geometria lumii înconjurătoare și a învățat rigoarea matematică a prezentării. Desigur, ambele aspecte ale frumuseții fractalilor sunt strâns legate între ele și nu se exclud, ci se completează reciproc, deși fiecare dintre ele este autosuficient.

Geometria fractala a naturii dupa Mandelbrot este o geometrie reala care satisface definitia geometriei propusa in Programul Erlangen de F. Klein. Cert este că înainte de apariția geometriei non-euclidiene N.I. Lobachevsky - L. Bolyai, a existat o singură geometrie - cea care a fost stabilită în „Principii”, iar întrebarea ce este geometria și care dintre geometrii este geometria lumii reale nu a apărut și nu a putut. apărea. Dar odată cu apariția unei alte geometrii, a apărut întrebarea ce este geometria în general și care dintre multele geometrii corespunde lumii reale. Potrivit lui F. Klein, geometria se ocupă cu studiul unor astfel de proprietăți ale obiectelor care sunt invariante la transformări: Euclidian - invarianți ai grupului de mișcări (transformări care nu modifică distanța dintre niciunul dintre două puncte, adică reprezentând o suprapunere de translații paralele). și rotații cu sau fără schimbarea orientării) , geometria lui Lobachevsky-Bolyai - invarianți ai grupului Lorentz. Geometria fractală se ocupă cu studiul invarianților grupului de transformări autoafine, i.e. proprietăți exprimate prin legile puterii.

În ceea ce privește corespondența cu lumea reală, geometria fractală descrie o clasă foarte largă de procese și fenomene naturale și, prin urmare, putem, după B. Mandelbrot, să vorbim pe bună dreptate despre geometria fractală a naturii. Nou - obiectele fractale au proprietăți neobișnuite. Lungimile, ariile și volumele unor fractali sunt zero, în timp ce altele se întorc la infinit.

Natura creează adesea fractali uimitori și frumoși, cu o geometrie ideală și o astfel de armonie încât pur și simplu îngheți de admirație. Și iată exemplele lor:

Scoici

Fulger admira cu frumusetea lor. Fractalii creați de fulgere nu sunt arbitrari sau regulați

Forma fractală subspecie de conopidă(Brassica cauliflora). Această specie particulară este un fractal deosebit de simetric.

Ferigă este, de asemenea, un bun exemplu de fractal printre floră.

Păuni toată lumea este cunoscută pentru penajul lor colorat, în care sunt ascunse fractali solide.

Gheață, modele geroase pe ferestre acestea sunt tot fractali

Din imaginea mărită frunze, inainte de ramuri de copac- fractalii pot fi găsiți în orice

Fractalii sunt peste tot și peste tot în natura din jurul nostru. Întregul Univers este construit după legi uimitor de armonioase cu precizie matematică. Este posibil după aceasta să ne gândim că planeta noastră este o concatenare aleatorie de particule? Cu greu.

Capitolul 4. Aplicarea fractalilor

Fractalii găsesc din ce în ce mai multe aplicații în știință. Motivul principal pentru aceasta este că ei descriu lumea reală uneori chiar mai bine decât fizica sau matematica tradițională. Aici sunt cateva exemple:

Unele dintre cele mai puternice aplicații ale fractalilor se află în grafica pe computer. Aceasta este compresia imaginii fractale. Fizica și mecanica modernă abia încep să studieze comportamentul obiectelor fractale.

Avantajele algoritmilor de compresie a imaginilor fractale sunt dimensiunea foarte mică a fișierului împachetat și timpul scurt de recuperare a imaginii. Imaginile fractale împachetate pot fi scalate fără apariția pixelării (calitate slabă a imaginii - pătrate mari). Dar procesul de compresie durează mult și uneori durează ore întregi. Algoritmul de ambalare cu pierderi fractale vă permite să setați nivelul de compresie, similar cu formatul jpeg. Algoritmul se bazează pe căutarea unor bucăți mari din imagine care sunt similare cu unele bucăți mici. Și numai piesa care este similară cu care este scrisă în fișierul de ieșire. La comprimare se folosește de obicei o grilă pătrată (piesele sunt pătrate), ceea ce duce la o ușoară angularitate la restaurarea imaginii; o grilă hexagonală nu are acest dezavantaj.

Iterated a dezvoltat un nou format de imagine, „Sting”, care combină compresia fractală și „wave” (cum ar fi jpeg) fără pierderi. Noul format vă permite să creați imagini cu posibilitatea de scalare ulterioară de înaltă calitate, iar volumul fișierelor grafice este de 15-20% din volumul imaginilor necomprimate.

În mecanică și fizică Fractalii sunt folosiți datorită proprietății lor unice de a repeta contururile multor obiecte naturale. Fractalii vă permit să aproximați copacii, suprafețele de munte și crăpăturile cu o precizie mai mare decât aproximările folosind seturi de segmente sau poligoane (cu aceeași cantitate de date stocate). Modelele fractale, ca și obiectele naturale, au o „rugozitate”, iar această proprietate este păstrată indiferent de cât de mare este mărirea modelului. Prezența unei măsuri uniforme pe fractali permite să se aplice integrarea, teoria potențialului și să le folosească în locul obiectelor standard în ecuațiile deja studiate.

Geometria fractală este, de asemenea, folosită pentru proiectarea dispozitivelor de antenă. Acesta a fost folosit pentru prima dată de inginerul american Nathan Cohen, care locuia atunci în centrul Bostonului, unde era interzisă instalarea de antene externe pe clădiri. Cohen a decupat o formă de curbă Koch din folie de aluminiu și apoi a lipit-o pe o bucată de hârtie și apoi a atașat-o la receptor. S-a dovedit că o astfel de antenă nu funcționează mai rău decât una obișnuită. Și deși principiile fizice ale unei astfel de antene nu au fost încă studiate, acest lucru nu l-a împiedicat pe Cohen să-și înființeze propria companie și să lanseze producția lor în serie. În prezent, compania americană „Fractal Antenna System” a dezvoltat un nou tip de antenă. Acum puteți înceta utilizarea antenelor externe proeminente în telefoanele mobile. Așa-numita antenă fractală este situată direct pe placa principală în interiorul dispozitivului.

Există, de asemenea, multe ipoteze despre utilizarea fractalilor - de exemplu, sistemele limfatic și circulator, plămânii și multe altele au și proprietăți fractale.

Capitolul 5. Lucrări practice.

Mai întâi, să ne uităm la fractalii „Colier”, „Victorie” și „Pătrat”.

În primul rând - "Colier"(Fig. 7). Inițiatorul acestui fractal este un cerc. Acest cerc este format dintr-un anumit număr de aceleași cercuri, dar de dimensiuni mai mici, și el însuși este unul dintre mai multe cercuri care sunt la fel, dar de dimensiuni mai mari. Deci procesul de educație este nesfârșit și se poate desfășura atât într-o direcție, cât și în sens invers. Acestea. figura poate fi mărită luând doar un arc mic, sau poate fi redusă luând în considerare construcția sa din altele mai mici.

orez. 7.

„Colier” fractal

Al doilea fractal este "Victorie"(Fig. 8). A primit acest nume pentru că arată ca litera latină „V”, adică „victorie”. Acest fractal constă dintr-un anumit număr de „vs” mici care formează un „V” mare, iar în jumătatea stângă, în care cele mici sunt așezate astfel încât jumătățile lor stângi să formeze o linie dreaptă, partea dreaptă este construită în la fel. Fiecare dintre acești „v” este construit în același mod și continuă acest lucru la infinit.

Fig.8. Fractal „Victorie”

Al treilea fractal este „Pătrat” (Fig. 9). Fiecare dintre laturile sale este formată dintr-un rând de celule, în formă de pătrate, ale căror laturi reprezintă și rânduri de celule etc.

Fig. 9. Fractal „Pătrat”

Fractalul a fost numit „Trandafir” (Fig. 10), datorită asemănării sale exterioare cu această floare. Construcția unui fractal presupune construirea unei serii de cercuri concentrice, a căror rază variază proporțional cu un raport dat (în acest caz, R m / R b = ¾ = 0,75.). După aceea, în fiecare cerc este înscris un hexagon regulat, a cărui latură este egală cu raza cercului descris în jurul lui.

Orez. 11. Fractal „Trandafir*”

În continuare, să trecem la un pentagon obișnuit, în care îi desenăm diagonalele. Apoi, în pentagonul rezultat la intersecția segmentelor corespunzătoare, desenăm din nou diagonalele. Să continuăm acest proces la infinit și să obținem fractalul „Pentagramă” (Fig. 12).

Să introducem un element de creativitate și fractalul nostru va lua forma unui obiect mai vizual (Fig. 13).

Orez. 12. Fractal „Pentagramă”.

Orez. 13. Fractal „Pentagramă *”

Orez. 14 fractali „Gaura neagră”

Experimentul nr. 1 „Arborele”

Acum că am înțeles ce este un fractal și cum să construiesc unul, am încercat să-mi creez propriile imagini fractale. În Adobe Photoshop, am creat o mică subrutină sau acțiune, particularitatea acestei acțiuni este că repetă acțiunile pe care le fac și așa obțin un fractal.

Pentru început, am creat un fundal pentru viitorul nostru fractal cu o rezoluție de 600 x 600. Apoi am desenat 3 linii pe acest fundal - baza viitorului nostru fractal.

CU Următorul pas este să scrieți scenariul.

duplicați stratul ( strat > duplicat) și schimbați tipul de amestecare la " Ecran" .

Hai sa-i spunem " fr1". Copiați acest strat (" fr1") de încă 2 ori.

Acum trebuie să trecem la ultimul strat (fr3) și îmbinați-l de două ori cu precedentul ( Ctrl+E). Reduceți luminozitatea stratului ( Imagine > Ajustări > Luminozitate/Contrast , luminozitate setată 50% ). Îmbinați din nou cu stratul anterior și tăiați marginile întregului desen pentru a elimina părțile invizibile. Am copiat această imagine, am făcut-o mai mică și am lipit-o peste alta, schimbând culoarea.

Ultimul pas a fost să copiați această imagine și să o lipiți mai mică și rotită. Acesta este rezultatul final.

Concluzie

Această lucrare este o introducere în lumea fractalilor. Am luat în considerare doar cea mai mică parte din ceea ce sunt fractalii și pe baza ce principii sunt construite.

Grafica fractală nu este doar un set de imagini care se repetă automat, este un model al structurii și principiului oricărui lucru existent. Întreaga noastră viață este reprezentată de fractali. Toată natura din jurul nostru este formată din ele. Este imposibil să nu remarcăm utilizarea pe scară largă a fractalilor în jocurile pe calculator, unde reliefurile de teren sunt adesea imagini fractale bazate pe modele tridimensionale ale unor seturi complexe. Fractalii facilitează foarte mult desenarea grafică pe computer; cu ajutorul fractalilor, sunt create multe efecte speciale, diverse imagini fabuloase și incredibile etc. De asemenea, copacii, norii, țărmurile și toate celelalte naturi sunt desenate folosind geometria fractală. Grafica fractală este necesară peste tot, iar dezvoltarea „tehnologiilor fractale” este una dintre sarcinile importante astăzi.

În viitor, intenționez să învăț cum să construiesc fractali algebrici odată ce studiez numerele complexe mai detaliat. De asemenea, vreau să încerc să-mi construiesc propriile imagini fractale în limbajul de programare Pascal folosind bucle.

Este demn de remarcat utilizarea fractalilor în tehnologia computerelor, în plus față de simpla construire a imaginilor frumoase pe ecranul computerului. Fractalii în tehnologia computerelor sunt utilizați în următoarele domenii:

1. Comprimarea imaginilor și a informațiilor

2. Ascunderea informațiilor din imagine, sunet,...

3. Criptarea datelor folosind algoritmi fractali

4. Realizarea muzicii fractale

5. Modelarea sistemului

Lucrarea noastră nu enumeră toate domeniile cunoașterii umane în care teoria fractalilor și-a găsit aplicarea. Vrem doar să spunem că nu a trecut mai mult de o treime de secol de când a apărut teoria, dar în acest timp fractalii pentru mulți cercetători au devenit o lumină strălucitoare bruscă în noapte, care a iluminat fapte și modele necunoscute până acum în anumite zone de date. . Cu ajutorul teoriei fractalilor, au început să explice evoluția galaxiilor și dezvoltarea celulelor, apariția munților și formarea norilor, mișcarea prețurilor la bursă și dezvoltarea societății și a familiei. Poate că, la început, această pasiune pentru fractali a fost chiar prea intensă și încercările de a explica totul folosind teoria fractalilor au fost nejustificate. Dar, fără îndoială, această teorie are dreptul să existe și regretăm că recent a fost cumva uitată și a rămas soarta elitei. În pregătirea acestei lucrări, a fost foarte interesant pentru noi să găsim aplicații ale TEORIEI în PRACTICĂ. Pentru că de foarte multe ori există sentimentul că cunoștințele teoretice se deosebesc de realitatea vieții.

Astfel, conceptul de fractali devine nu numai o parte a științei „pure”, ci și un element al culturii umane universale. Știința fractală este încă foarte tânără și are un viitor mare în față. Frumusețea fractalilor este departe de a fi epuizată și încă ne va oferi multe capodopere - cele care încântă ochiul și cele care aduc adevărată plăcere minții.

10. Referințe

Bozhokin S.V., Parshin D.A. Fractali și multifractali. RHD 2001 .

Vitolin D. Aplicarea fractalilor în grafica computerizată. // Computerworld-Rusia.-1995

Mandelbrot B. Seturi de fractali autoafine, „Fractali în fizică”. M.: Mir 1988

Mandelbrot B. Geometria fractală a naturii. - M.: „Institutul de Cercetări Informatice”, 2002.

Morozov A.D. Introducere în teoria fractalilor. N. Novgorod: Editura Nijni Novgorod. Universitatea 1999

Peitgen H.-O., Richter P. H. Frumusețea fractalilor. - M.: „Mir”, 1993.

Resurse de internet

http://www.ghcube.com/fractals/determin.html

http://fractals.nsu.ru/fractals.chat.ru/

http://fractals.nsu.ru/animations.htm

http://www.cootey.com/fractals/index.html

http://fraktals.ucoz.ru/publ

http://sakva.narod.ru

http://rusnauka.narod.ru/lib/author/kosinov_n/12/

http://www.cnam.fr/fractals/

http://www.softlab.ntua.gr/mandel/

http://subscribe.ru/archive/job.education.maths/201005/06210524.html

Haosul este ordinea care trebuie descifrată.

Jose Saramago, „Dublul”

„Pentru generațiile viitoare, secolul al XX-lea va fi amintit doar pentru crearea teoriilor relativității, mecanicii cuantice și haosului... teoria relativității a eliminat iluziile lui Newton despre spațiu-timp absolut, mecanica cuantică a spulberat visul determinismul evenimentelor fizice și, în cele din urmă, haosul a dezmințit fantezia lui Laplace de predeterminare completă a dezvoltării sistemelor.” Aceste cuvinte ale celebrului istoric și popularizator al științei american James Gleick reflectă importanța enormă a problemei, care este doar pe scurt tratată în articolul adus în atenția cititorului. Lumea noastră a apărut din haos. Totuși, dacă haosul nu s-ar supune propriilor legi, dacă nu ar exista o logică specială în el, nu ar putea genera nimic.

Noul este bine uitat vechi

Permiteți-mi să mai citez unul din Gleick:

Gândul la asemănarea interioară, că marele poate fi înglobat în mic, a mângâiat de mult sufletul omului... Potrivit lui Leibniz, o picătură de apă conține întreaga lume sclipitoare de culori, unde stropii de apă scânteie și trăiesc alte universuri necunoscute. . „Vezi lumea într-un grăunte de nisip”, a strigat Blake, iar unii oameni de știință au încercat să-i urmeze ordinul. Primii cercetători ai lichidului seminal au avut tendința de a vedea în fiecare spermatozoid un fel de homunculus, adică o persoană minusculă, dar complet formată.

Retrospectiva unor astfel de opinii poate fi transformată mult mai departe în istorie. Unul dintre principiile de bază ale magiei - o etapă integrală a dezvoltării oricărei societăți - este postulatul: o parte este asemănătoare întregului. S-a manifestat în acțiuni precum îngroparea craniului unui animal în locul întregului animal, a unui model de car în locul carului însuși etc. Prin păstrarea craniului unui strămoș, rudele credeau că el a continuat să locuiască alături de ei. și să ia parte la treburile lor.

Chiar și filozoful grec antic Anaxagoras considera elementele primare ale universului ca niște particule asemănătoare cu alte particule ale întregului și întregului însuși, „infinite atât în mulțime, cât și în micime”. Aristotel a caracterizat elementele lui Anaxagoras cu adjectivul „asemănător cu părțile”.

Iar contemporanul nostru, ciberneticianul american Ron Eglash, explorând cultura triburilor africane și a indienilor din America de Sud, a făcut o descoperire: încă din cele mai vechi timpuri, unii dintre ei au folosit principii fractale de construcție în ornamente, modele aplicate îmbrăcămintei și articolelor de uz casnic, în bijuterii. , ceremonii rituale și chiar în arhitectură. Astfel, structura satelor unor triburi africane este un cerc în care sunt mici cercuri - case, în interiorul cărora sunt și mai mici cercuri - case ale spiritelor. Pentru alte triburi, în loc de cercuri, alte figuri servesc drept elemente arhitecturale, dar ele se repetă și la scări diferite, subordonate unei singure structuri. Mai mult, aceste principii de construcție nu erau o simplă imitație a naturii, ci erau în concordanță cu viziunea asupra lumii și organizarea socială existente.

Civilizația noastră, s-ar părea, s-a mutat departe de existența primitivă. Totuși, continuăm să trăim în aceeași lume; suntem încă înconjurați de natură, trăind după propriile legi, în ciuda tuturor încercărilor umane de a o adapta la nevoile noastre. Și omul însuși (să nu uităm de asta) rămâne parte din această natură.

Gert Eilenberger, un fizician german care a început să studieze neliniaritatea, a remarcat odată:

De ce silueta unui copac gol este îndoită sub presiunea unui vânt de furtună pe fundalul unui cer posomorât de iarnă percepută ca fiind frumoasă, dar contururile unei clădiri moderne multifuncționale, în ciuda tuturor eforturilor arhitectului, nu par așa la toate? Mi se pare că... simțul nostru de frumos este „alimentat” de îmbinarea armonioasă a ordinii și a dezordinei, care poate fi observată în fenomenele naturale: nori, copaci, lanțuri muntoase sau cristale de fulgi de nea. Toate astfel de contururi sunt procese dinamice înghețate în forme fizice și o combinație de stabilitate și haos este tipică pentru ele.

La originile teoriei haosului

Ce ne referim prin haos? Incapacitatea de a prezice comportamentul sistemului, salturi aleatorii în direcții diferite care nu se vor transforma niciodată într-o secvență ordonată.

Primul cercetător al haosului este matematicianul, fizicianul și filozoful francez Henri Poincaré. Înapoi la sfârșitul secolului al XIX-lea. În timp ce studia comportamentul unui sistem cu trei corpuri care interacționează gravitațional, el a observat că ar putea exista orbite non-periodice care nu se îndepărtează constant de un anumit punct și nici nu se apropie de el.

Metodele tradiționale de geometrie, utilizate pe scară largă în științele naturii, se bazează pe aproximarea structurii obiectului studiat cu figuri geometrice, de exemplu linii, plane, sfere, ale căror dimensiuni metrice și topologice sunt egale între ele. În cele mai multe cazuri, proprietățile obiectului studiat și interacțiunea acestuia cu mediul sunt descrise prin caracteristici termodinamice integrale, ceea ce duce la pierderea unei părți semnificative a informațiilor despre sistem și înlocuirea acestuia cu un model mai mult sau mai puțin adecvat. Cel mai adesea, o astfel de simplificare este complet justificată, dar există numeroase situații în care utilizarea modelelor inadecvate din punct de vedere topologic este inacceptabilă. Un exemplu de astfel de discrepanță a fost dat în teza candidatului său (acum doctor în științe chimice) de Vladimir Konstantinovich Ivanov: este detectat la măsurarea ariei suprafeței dezvoltate (de exemplu, poroase) a solidelor folosind sorbția. metode care înregistrează izotermele de adsorbție. S-a dovedit că mărimea zonei depinde de dimensiunea liniară a moleculelor „de măsurare” nu pătratic, ceea ce ar fi de așteptat din cele mai simple considerații geometrice, dar cu un exponent, uneori foarte apropiat de trei.

Prognoza meteo este una dintre problemele cu care s-a luptat omenirea din cele mai vechi timpuri. Există o glumă binecunoscută pe această temă, în care prognoza meteo este transmisă de-a lungul unui lanț de la un șaman - la un păstor de reni, apoi la un geolog, apoi la redactorul unui program de radio și, în cele din urmă, cercul este închis, întrucât se dovedeşte că şamanul a aflat prognoza de la radio. Descrierea unui sistem complex precum vremea, cu multe variabile, nu poate fi redusă la simple modele. Această problemă a început utilizarea computerelor pentru modelarea sistemelor dinamice neliniare. Unul dintre fondatorii teoriei haosului, meteorologul și matematicianul american Edward Norton Lorenz a dedicat mulți ani problemei prognozării meteo. În anii 60 ai secolului trecut, încercând să înțeleagă motivele lipsei de încredere a prognozelor meteo, el a arătat că starea unui sistem dinamic complex poate depinde în mare măsură de condițiile inițiale: o ușoară modificare a unuia dintre mulți parametri se poate schimba radical. rezultatul scontat. Lorenz a numit această dependență efectul fluture: „Fâlfâitul aripilor unei molii de astăzi la Beijing ar putea provoca un uragan în New York într-o lună”. Lucrările sale privind circulația generală a atmosferei i-au adus faimă. Studiind sistemul de ecuații cu trei variabile care descriu procesul, Lorenz a afișat grafic rezultatele analizei sale: liniile graficului reprezintă coordonatele punctelor determinate de soluțiile în spațiul acestor variabile (Fig. 1). Helixul dublu rezultat, numit atractor Lorentz(sau „atractor ciudat”), arăta ca ceva la nesfârșit confuz, dar mereu situat în anumite limite și care nu se repetă niciodată. Mișcarea într-un atractor este abstractă (variabilele pot fi viteza, densitatea, temperatura etc.) și totuși transmite caracteristicile fenomenelor fizice reale, cum ar fi mișcarea unei roți de apă, convecția într-o buclă închisă, radiația dintr-un laser monomod, oscilații armonice disipative (ai căror parametri joacă rolul variabilelor corespunzătoare).

Dintre miile de publicații care alcătuiesc literatura de specialitate despre problema haosului, este puțin probabil ca vreuna să fi fost citată mai des decât articolul „Flux non-periodic determinist” scris de Lorentz în 1963. Deși modelarea computerizată transformase deja prognoza meteo dintr-o „artă într-o știință” la momentul acestei lucrări, prognozele pe termen lung erau încă nesigure și nesigure. Motivul a fost același efect de fluture.

În aceiași ani 60, matematicianul Stephen Smail de la Universitatea din California a adunat la Berkeley un grup de cercetare format din tineri cu idei similare. El a primit anterior medalia Fields pentru cercetările sale remarcabile în topologie. Smale a studiat sistemele dinamice, în special oscilatorii haotici neliniari. Pentru a reproduce toată dezordinea oscilatorului van der Pol în spațiul fazelor, el a creat o structură cunoscută sub numele de „potcoavă” - un exemplu de sistem dinamic care are o dinamică haotică.

„Pocoava” (Fig. 2) este o imagine precisă și vizibilă a unei puternice dependențe de condițiile inițiale: nu veți ghici niciodată unde va fi punctul de plecare după mai multe iterații. Acest exemplu a fost impulsul pentru inventarea „difereomorfismelor Anosov” de către matematicianul rus, specialist în teoria sistemelor dinamice și a ecuațiilor diferențiale, geometrie și topologie diferențială, Dmitri Viktorovich Anosov. Mai târziu, din aceste două lucrări a crescut teoria sistemelor dinamice hiperbolice. A durat un deceniu înainte ca lucrările lui Smale să ajungă în atenția altor discipline. „Când s-a întâmplat acest lucru, fizicienii și-au dat seama că Smail a transformat o întreagă ramură a matematicii pentru a se confrunta cu lumea reală.”

În 1972, matematicianul de la Universitatea din Maryland, James York, a citit lucrarea lui Lorentz menționată mai sus și l-a surprins. York a văzut un model fizic viu în articol și a considerat că era de datoria lui sacră să transmită fizicienilor ceea ce ei nu văzuseră în lucrările lui Lorentz și Smail. I-a transmis lui Smail o copie a articolului lui Lorenz. A fost uimit să descopere că un meteorolog necunoscut (Lorentz) cu zece ani mai devreme descoperise tulburarea pe care el însuși o considerase cândva incredibilă din punct de vedere matematic și a trimis copii tuturor colegilor săi.

Biologul Robert May, un prieten al lui York, studia schimbările în populațiile de animale. May a mers pe urmele lui Pierre Verchlust, care în 1845 a atras atenția asupra impredictibilității modificărilor numărului de animale și a ajuns la concluzia că rata de creștere a populației nu este o valoare constantă. Cu alte cuvinte, procesul se dovedește a fi neliniar. May a încercat să surprindă ce se întâmplă cu o populație atunci când fluctuațiile coeficientului de creștere se apropie de un anumit punct critic (punctul de bifurcație). Variind valorile acestui parametru neliniar, el a descoperit că schimbări fundamentale sunt posibile în însăși esența sistemului: o creștere a parametrului a însemnat o creștere a gradului de neliniaritate, care, la rândul său, a schimbat nu numai cantitativ. , dar și caracteristicile calitative ale rezultatului. O astfel de operațiune a influențat atât valoarea finală a mărimii populației aflate în echilibru, cât și capacitatea acesteia de a realiza în general aceasta din urmă. În anumite condiții, periodicitatea a lăsat loc haosului, oscilațiilor care nu s-au stins niciodată.

York a analizat matematic fenomenele descrise în lucrarea sa, demonstrând că în orice sistem unidimensional se întâmplă următoarele: dacă apare un ciclu regulat cu trei valuri (creșteri și scăderi netede în valorile oricărui parametru), atunci în viitor, sistemul va începe să demonstreze cât de regulate cicluri de orice altă durată , și complet haotic. (După cum s-a dovedit la câțiva ani după publicarea articolului la o conferință internațională din Berlinul de Est, matematicianul sovietic (ucrainean) Alexander Nikolaevici Sharkovsky a fost oarecum înaintea lui York în cercetările sale). York a scris un articol pentru celebra publicație științifică American Mathematical Monthly. Cu toate acestea, York a obținut mai mult decât un simplu rezultat matematic: le-a demonstrat fizicienilor că haosul este omniprezent, stabil și structurat. El a dat motive să creadă că sistemele complexe, descrise în mod tradițional prin ecuații diferențiale greu de rezolvat, pot fi reprezentate folosind grafice vizuale.

May a încercat să atragă atenția biologilor asupra faptului că populațiile de animale experimentează mai mult decât cicluri ordonate. Pe drumul către haos, apare o întreagă cascadă de dublare a perioadei. În punctele de bifurcație, o ușoară creștere a fertilității indivizilor ar putea duce, de exemplu, la înlocuirea ciclului de patru ani al populației de molii țigănești cu un ciclu de opt ani. Americanul Mitchell Feigenbaum a decis să înceapă prin a calcula valorile exacte ale parametrului care a dat naștere unor astfel de modificări. Calculele sale au arătat că nu contează care era populația inițială - încă se apropia constant de atractor. Apoi, odată cu prima dublare a perioadelor, atractorul, ca o celulă care se divide, s-a bifurcat. Apoi a avut loc următoarea multiplicare a perioadelor și fiecare punct atractor a început să se împartă din nou. Numărul - un invariant obținut de Feigenbaum - i-a permis să prezică exact când se va întâmpla asta. Omul de știință a descoperit că ar putea prezice acest efect pentru cel mai complex atractor - la două, patru, opt puncte... Vorbind în limbajul ecologiei, el ar putea prezice numărul real care se realizează în populații în timpul fluctuațiilor anuale. Așa că Feigenbaum a descoperit „cascada de dublare a perioadei” în 1976, bazându-se pe munca lui May și pe cercetările sale asupra turbulenței. Teoria lui a reflectat o lege naturală care se aplică tuturor sistemelor care se confruntă cu o tranziție de la o stare ordonată la haos. York, May și Feigenbaum au fost primii din Occident care au înțeles pe deplin importanța dublării perioadei și au reușit să transmită această idee întregii comunități științifice. May a afirmat că haosul trebuie învățat.

Matematicienii și fizicienii sovietici au avansat în cercetarea lor independent de colegii lor străini. Studiul haosului a început cu munca lui A. N. Kolmogorov în anii 50. Dar ideile colegilor străini nu au trecut neobservate. Pionierii teoriei haosului sunt considerați a fi matematicienii sovietici Andrei Nikolaevici Kolmogorov și Vladimir Igorevici Arnold și matematicianul german Jurgen Moser, care au construit teoria haosului numită KAM (teoria Kolmogorov-Arnold-Moser). Un alt dintre compatrioții noștri remarcabili, genialul fizician și matematician Yakov Grigorievich Sinai, a aplicat în termodinamică considerații asemănătoare cu „Pocoava de cal”. De îndată ce fizicienii occidentali au făcut cunoștință cu opera lui Lorentz în anii 70, aceasta a devenit faimoasă în URSS. În 1975, în timp ce York și May făceau încă eforturi considerabile pentru a capta atenția colegilor lor, Sinai și tovarășii săi au organizat un grup de cercetare la Gorki pentru a studia această problemă.

În secolul trecut, când specializarea îngustă și separarea între diverse discipline au devenit norma în știință, matematicienii, fizicienii, biologii, chimiștii, fiziologii și economiștii s-au luptat cu probleme similare fără să se audă. Ideilor care necesită o schimbare a viziunii obișnuite asupra lumii le este întotdeauna greu să-și găsească drumul. Cu toate acestea, a devenit treptat clar că lucruri precum schimbările populațiilor de animale, fluctuațiile prețurilor pieței, schimbările vremii, distribuția corpurilor cerești în funcție de dimensiune și multe, multe altele, sunt supuse acelorași modele. „Conștientizarea acestui fapt i-a forțat pe manageri să-și reconsidere atitudinea față de asigurări, pe astronomi să privească sistemul solar dintr-un unghi diferit și pe politicieni să-și schimbe părerea despre cauzele conflictelor armate.”

La mijlocul anilor '80 situația se schimbase foarte mult. Ideile geometriei fractale au unit oamenii de știință care erau nedumeriți de propriile lor observații și nu știau cum să le interpreteze. Pentru cercetătorii haosului, matematica a devenit o știință experimentală, iar computerele au înlocuit laboratoarele. Imaginile grafice au devenit de o importanță capitală. Noua știință a oferit lumii un limbaj special, concepte noi: portret de fază, atractor, bifurcare, secțiune a spațiului de fază, fractal...

Benoit Mandelbrot, bazându-se pe ideile și lucrările predecesorilor și contemporanilor săi, a arătat că procese atât de complexe precum creșterea unui copac, formarea norilor, variațiile caracteristicilor economice sau dimensiunea populațiilor de animale sunt guvernate de legi ale naturii în esență similare. . Acestea sunt anumite tipare după care trăiește haosul. Din punctul de vedere al auto-organizării naturale, ele sunt mult mai simple decât formele artificiale familiare oamenilor civilizați. Ele pot fi considerate complexe doar în contextul geometriei euclidiene, deoarece fractalii sunt determinați prin specificarea unui algoritm și, prin urmare, pot fi descriși folosind o cantitate mică de informații.

Geometria fractală a naturii

Să încercăm să ne dăm seama ce este un fractal și cu ce se mănâncă. Și, de fapt, puteți mânca unele dintre ele, cum ar fi reprezentantul tipic prezentat în fotografie.

Cuvânt fractal provine din latină fractus - zdrobit, spart, spart în bucăți. Un fractal este o mulțime matematică care are proprietatea auto-asemănării, adică invarianța la scară.

Termenul „fractal” a fost inventat de Mandelbrot în 1975 și a câștigat popularitate pe scară largă odată cu publicarea cărții sale din 1977 The Fractal Geometry of Nature. „Dă-i monstrului un nume confortabil și familiar și vei fi surprins cât de ușor va fi să-l îmblânzești!” – spuse Mandelbrot. Această dorință de a face obiectele studiate (mulțimile matematice) apropiate și de înțeles a dus la nașterea de noi termeni matematici, precum praf, brânză de vacă, ser, demonstrând clar legătura lor profundă cu procesele naturale.

Conceptul matematic al unui fractal identifică obiectele care au structuri de diferite scări, atât mari cât și mici, și reflectă astfel principiul ierarhic de organizare. Desigur, diferite ramuri ale unui copac, de exemplu, nu pot fi aliniate exact unele cu altele, dar pot fi considerate similare în sens statistic. În același mod, formele norilor, contururile munților, linia coastei mării, modelul flăcărilor, sistemul vascular, ravenele, fulgerele, privite la diferite scări, arată similar. Deși această idealizare poate fi o simplificare a realității, ea crește semnificativ profunzimea descrierii matematice a naturii.

Mandelbrot a introdus conceptul de „fractal natural” pentru a desemna structuri naturale care pot fi descrise folosind seturi de fractali. Aceste obiecte naturale includ un element de hazard. Teoria creată de Mandelbrot face posibilă descrierea cantitativă și calitativă a tuturor acelor forme care au fost numite anterior încurcate, ondulate, aspre etc.

Procesele dinamice discutate mai sus, așa-numitele procese de feedback, apar în diverse probleme fizice și matematice. Toți au un lucru în comun - competiția între mai mulți centri (numiți „atractori”) pentru dominația în avion. Starea în care se află sistemul după un anumit număr de iterații depinde de „locul său de pornire”. Prin urmare, fiecărui atractor îi corespunde o anumită regiune de stări inițiale, din care sistemul va cădea în mod necesar în starea finală luată în considerare. Astfel, spațiul de fază al sistemului (spațiul abstract al parametrilor asociați unui sistem dinamic specific, punctele în care caracterizează în mod unic toate stările sale posibile) este împărțit în zone de atractie atractori. Există o întoarcere deosebită la dinamica lui Aristotel, conform căreia fiecare corp tinde către locul său destinat. Granițele simple între „teritoriile învecinate” apar rareori ca urmare a unei astfel de rivalități. În această zonă de graniță are loc trecerea de la o formă de existență la alta: de la ordine la haos. Forma generală a expresiei pentru legea dinamică este foarte simplă: x n+1 → f x n C . Întreaga dificultate constă în relația neliniară dintre valoarea inițială și rezultat. Dacă începeți un proces iterativ de tipul indicat de la o valoare arbitrară \(x_0\), atunci rezultatul acestuia va fi secvența \(x_1\), \(x_2\), ..., care fie va converge către o anumită limitare. valoarea \(X\) , luptă pentru o stare de odihnă, fie va ajunge la un anumit ciclu de valori care se va repeta din nou și din nou, fie se va comporta neregulat și imprevizibil tot timpul. Tocmai astfel de procese au fost studiate de matematicienii francezi Gaston Julia și Pierre Fateau în timpul Primului Război Mondial.

Studiind seturile pe care le-au descoperit, Mandelbrot în 1979 a ajuns să înfățișeze o imagine pe plan complex, care este, după cum va fi clar din cele ce urmează, un fel de cuprins pentru o întreagă clasă de forme numite seturi Julia. Mulțimea Julia este o mulțime de puncte care apar ca urmare a iterației transformării pătratice: x n → x n−1 2 + C, dinamica în vecinătatea cărora este instabilă în raport cu micile perturbări ale poziției inițiale. Fiecare valoare succesiva a lui \(x\) se obtine din cea precedenta; se numeste numarul complex \(C\). parametru de control. Comportamentul șirului de numere depinde de parametrul \(C\) și de punctul de plecare \(x_0\). Dacă fixăm \(C\) și modificăm \(x_0\) în câmpul numerelor complexe, obținem setul Julia. Dacă fixăm \(x_0\) = 0 și modificăm \(C\), obținem mulțimea Mandelbrot (\(M\)). Ne spune la ce fel de set Julia ar trebui să ne așteptăm pentru o anumită alegere a \(C\). Fiecare număr complex \(C\) fie aparține regiunii \(M\) (negru în Fig. 3), fie nu. \(C\) aparține lui \(M\) dacă și numai dacă „punctul critic” \(x_0\) = 0 nu tinde spre infinit. Mulțimea \(M\) constă din toate punctele \(C\) care sunt asociate cu mulțimi Julia conexe, dar dacă un punct \(C\) se află în afara mulțimii \(M\), mulțimea Julia asociată acestuia este deconectat. Granița mulțimii \(M\) determină momentul tranziției de fază matematică pentru mulțimile Julia x n → x n−1 2 + C . Când parametrul \(C\) părăsește \(M\), seturile Julia își pierd conectivitatea, la figurat vorbind, explodează și se transformă în praf. Saltul calitativ care are loc la limita \(M\) afectează și regiunea adiacentă graniței. Structura dinamică complexă a regiunii de frontieră poate fi reprezentată aproximativ prin pictarea (condițional) în culori diferite a zonelor cu același timp de „fuire la infinit a punctului inițial \(x_0\) = 0”. Acele valori ale \(C\) (o nuanță) pentru care punctul critic necesită un număr dat de iterații care să fie în afara cercului de rază \(N\) umple golul dintre cele două linii. Pe măsură ce ne apropiem de limita \(M\), numărul necesar de iterații crește. Punctul este din ce în ce mai forțat să hoinărească de-a lungul potecilor întortocheate din apropierea ansamblului Julia. Setul Mandelbrot întruchipează procesul de tranziție de la ordine la haos.

Este interesant de urmărit calea pe care a urmat-o Mandelbrot către descoperirile sale. Benoit s-a născut la Varșovia în 1924; în 1936 familia a emigrat la Paris. După ce a absolvit Ecole Polytechnique și apoi Universitatea din Paris, Mandelbrot s-a mutat în SUA, unde a studiat și la California Institute of Technology. În 1958, a luat un loc de muncă la centrul de cercetare din Yorktown al IBM. În ciuda activităților pur aplicate ale companiei, poziția sa i-a permis să efectueze cercetări într-o varietate de domenii. Lucrând în domeniul economiei, tânărul specialist a început să studieze statisticile prețurilor bumbacului pe o perioadă lungă de timp (mai mult de 100 de ani). Analizând simetria fluctuațiilor de preț pe termen lung și pe termen scurt, el a observat că aceste fluctuații din timpul zilei păreau aleatorii și imprevizibile, dar succesiunea unor astfel de modificări nu depindea de scară. Pentru a rezolva această problemă, el a folosit pentru prima dată dezvoltările sale ale viitoarei teorii fractale și afișarea grafică a proceselor studiate.

Interesat de o varietate de domenii ale științei, Mandelbrot s-a îndreptat către lingvistica matematică, apoi a venit rândul teoriei jocurilor. El și-a propus, de asemenea, propria abordare a economiei, subliniind ordinea de scară în răspândirea orașelor mici și mari. În timp ce studia o lucrare puțin cunoscută a savantului englez Lewis Richardson, publicată după moartea autorului, Mandelbrot a întâlnit fenomenul litoralului. În articolul „Cât de lungă este coasta Marii Britanii?” el explorează în detaliu această întrebare, la care puțini oameni s-au gândit până acum, și ajunge la concluzii neașteptate: lungimea liniei de coastă este... infinit! Cu cât încerci să-l măsori mai precis, cu atât valoarea lui devine mai mare!

Pentru a descrie astfel de fenomene, Mandelbrot a venit cu ideea de dimensiune. Dimensiunea fractală a unui obiect servește ca o caracteristică cantitativă a uneia dintre trăsăturile sale, și anume, umplerea spațiului său.

Definiția conceptului de dimensiune fractală datează din lucrarea lui Felix Hausdorff, publicată în 1919, și a fost în cele din urmă formulată de Abram Samoilovici Besikovici. Dimensiunea fractală este o măsură a detaliilor, ruperii și neuniformității unui obiect fractal. În spațiul euclidian, dimensiunea topologică este întotdeauna determinată de un număr întreg (dimensiunea unui punct este 0, o dreaptă este 1, un plan este 2, un corp volumetric este 3). Dacă urmăriți, de exemplu, proiecția pe planul de mișcare a unei particule browniene, care pare să fie formată din segmente drepte, adică să aibă dimensiunea 1, se va dovedi foarte curând că urma sa umple aproape întregul plan. Dar dimensiunea planului este 2. Discrepanța dintre aceste mărimi ne dă dreptul de a clasifica această „curbă” drept fractal și de a numi dimensiunea sa intermediară (fracțională) fractal. Dacă luăm în considerare mișcarea haotică a unei particule într-un volum, dimensiunea fractală a traiectoriei va fi mai mare de 2, dar mai mică de 3. Arterele umane, de exemplu, au o dimensiune fractală de aproximativ 2,7. Rezultatele lui Ivanov menționate la începutul articolului referitoare la măsurarea ariei porilor a gelului de silice, care nu poate fi interpretată în cadrul conceptelor euclidiene convenționale, găsesc o explicație rezonabilă atunci când se utilizează teoria fractalilor.

Deci, din punct de vedere matematic, un fractal este o mulțime pentru care dimensiunea Hausdorff-Besicovich este strict mai mare decât dimensiunea sa topologică și poate fi (și cel mai adesea este) fracționară.

Trebuie subliniat în special faptul că dimensiunea fractală a unui obiect nu descrie forma acestuia, iar obiectele care au aceeași dimensiune, dar generate de mecanisme de formare diferite, sunt adesea complet diferite unele de altele. Fractalii fizici sunt mai degrabă auto-similari statistic.

Măsurarea fracționată permite calcularea unor caracteristici care nu pot fi clar determinate altfel: gradul de denivelare, discontinuitate, rugozitate sau instabilitate a unui obiect. De exemplu, o coastă întortocheată, în ciuda lungimii sale incomensurabile, are o rugozitate unică. Mandelbrot a indicat modalități de a calcula măsurători fracționale ale obiectelor din realitatea înconjurătoare. În crearea geometriei sale, el a propus o lege despre formele dezordonate care apar în natură. Legea spunea: gradul de instabilitate este constant la diferite scări.

Un tip special de fractali sunt fractali de timp. În 1962, Mandelbrot s-a confruntat cu sarcina de a elimina zgomotul din liniile telefonice care provoca probleme modemurilor computerelor. Calitatea transmisiei semnalului depinde de probabilitatea apariției erorilor. Inginerii s-au luptat cu problema reducerii zgomotului, venind cu tehnici uluitoare și costisitoare, dar nu au obținut rezultate impresionante. Pe baza lucrărilor fondatorului teoriei mulțimilor, Georg Cantor, Mandelbrot a arătat că apariția zgomotului - produsul haosului - nu poate fi evitată în principiu, prin urmare metodele propuse de a le trata nu vor aduce rezultate. În căutarea unui model în apariția zgomotului, el primește „Praful Cantor” - o secvență fractală de evenimente. În mod interesant, distribuția stelelor în Galaxie urmează aceleași modele:

„Materia”, distribuită uniform de-a lungul inițiatorului (un singur segment al axei timpului), este expusă unui vortex centrifugal, care o „mătură” până la treimi extreme ale intervalului... Coagulare poate fi numită orice cascadă de stări instabile, conducând în cele din urmă la o îngroșare a materiei, și termenul brânză de vacă poate determina volumul în interiorul căruia o anumită caracteristică fizică devine – ca urmare a coagulării – extrem de concentrată.

Fenomenele haotice, cum ar fi turbulența atmosferică, mobilitatea crustalei etc., prezintă un comportament similar la diferite scări de timp, la fel cum obiectele invariante la scară prezintă modele structurale similare la diferite scări spațiale.

Ca exemplu, vom oferi câteva situații tipice în care este util să folosim idei despre structura fractală. Profesorul de la Universitatea Columbia, Christopher Scholz, s-a specializat în studierea formei și structurii materiei solide a Pământului și a studiat cutremurele. În 1978, a citit cartea lui Mandelbrot Fractals: Shape, Randomness and Dimension » și a încercat să aplice teoria la descrierea, clasificarea și măsurarea obiectelor geofizice. Scholz a descoperit că geometria fractală a oferit științei o metodă eficientă de descriere a peisajului particular de bulgări al Pământului. Dimensiunea fractală a peisajelor planetei deschide ușa pentru înțelegerea celor mai importante caracteristici ale acesteia. Metalurgiștii au descoperit același lucru la o altă scară - pe suprafețele diferitelor tipuri de oțel. În special, dimensiunea fractală a unei suprafețe metalice ne permite adesea să judecăm rezistența acesteia. Un număr mare de obiecte fractale produc fenomenul de cristalizare. Cel mai comun tip de fractali care apar în timpul creșterii cristalelor sunt dendritele; acestea sunt extrem de răspândite în natura vie. Ansamblurile de nanoparticule demonstrează adesea implementarea „prafului Lewy”. Aceste ansambluri se combină cu solventul absorbit pentru a forma compacte transparente - ochelari Lewy, materiale fotonice potențial importante.

Întrucât fractalii nu sunt exprimați în forme geometrice primare, ci în algoritmi, seturi de proceduri matematice, este clar că această zonă a matematicii a început să se dezvolte odată cu apariția și dezvoltarea computerelor puternice. Haosul, la rândul său, a dat naștere la noi tehnologii informatice, tehnologie grafică specială care este capabilă să reproducă structuri uimitoare de o complexitate incredibilă generate de anumite tipuri de tulburări. În epoca internetului și a computerelor personale, ceea ce era destul de dificil pe vremea lui Mandelbrot a devenit ușor accesibil oricui. Dar cel mai important lucru din teoria sa a fost, desigur, nu crearea de imagini frumoase, ci concluzia că acest aparat matematic este potrivit pentru a descrie fenomene și procese naturale complexe care nu fuseseră deloc luate în considerare anterior în știință. Repertoriul elementelor algoritmice este inepuizabil.

Odată ce stăpânești limbajul fractalilor, poți descrie forma unui nor la fel de clar și simplu așa cum un arhitect descrie o clădire folosind desene care folosesc limbajul geometriei tradiționale.<...>Au trecut doar câteva decenii de când Benoit Mandelbrot a declarat: „Geometria naturii este fractală!” Astăzi putem deja presupune mult mai mult, și anume că fractalitatea este principiul primar de construcție a tuturor obiectelor naturale fără excepție.

În concluzie, permiteți-mi să vă prezint atenției un set de fotografii care ilustrează această concluzie și fractali construiți folosind un program de calculator Explorator de fractali. Următorul nostru articol va fi dedicat problemei utilizării fractalilor în fizica cristalelor.

Post Scriptum

Din 1994 până în 2013, o lucrare unică a oamenilor de știință autohtoni, „Atlasul variațiilor temporale în procesele antropogenice și sociale naturale”, a fost publicată în cinci volume - o sursă de materiale de neegalat care include date de monitorizare a spațiului, biosferei, litosferei, atmosferei, hidrosferei. , sfere sociale și tehnogene și sfere legate de sănătatea umană și calitatea vieții. Textul oferă detalii despre datele și rezultatele prelucrării acestora și compară caracteristicile dinamicii seriilor de timp și fragmentele acestora. O prezentare unificată a rezultatelor face posibilă obținerea de rezultate comparabile pentru a identifica caracteristicile comune și individuale ale dinamicii proceselor și relațiile cauză-efect dintre acestea. Materialul experimental arată că procesele din diferite domenii sunt, în primul rând, similare și, în al doilea rând, mai mult sau mai puțin conectate între ele.

Așadar, atlasul a rezumat rezultatele cercetării interdisciplinare și a prezentat o analiză comparativă a datelor complet diferite pe o gamă largă de timp și spațiu. Cartea arată că „procesele care au loc în sferele terestre sunt cauzate de un număr mare de factori care interacționează, care în diferite zone (și în momente diferite) provoacă reacții diferite”, ceea ce indică „necesitatea unei abordări integrate a analizei observații geodinamice, cosmice, sociale, economice și medicale" Rămâne de exprimat speranța că această activitate fundamental importantă va fi continuată.

. Jurgens H., Peitgen H.-O., Zaupe D. Limbajul fractalilor // În lumea științei. 1990. Nr. 10. p. 36–44.
. Atlas al variațiilor temporale ale proceselor naturale antropice și sociale. T. 1: Ordinea si haosul in litosfera si alte sfere. M., 1994; T. 2: Dinamica ciclică în natură și societate. M., 1998; T. 3: Sferele naturale și sociale ca părți ale mediului și ca obiecte de influență. M., 2002; T. 4: Omul și cele trei medii ale sale. M., 2009. T. 5: Omul și cele trei medii ale sale. M., 2013.

Conferința științifică deschisă regională Stavropol pentru școlari

Sectiunea: matematica

Denumirea funcției:Studiul caracteristicilor modelelor fractale pentru aplicare practică

9614524388, vkel -72@ Poștă . ru

Loc de munca : stația Grigoropolisskaya

Instituție de învățământ municipal școala Gimnazială Nr.2, clasa a VIII-a.

Consilier stiintific: Kuznetsova Elena

Ivanovna, profesor de matematică și informatică

Instituție de învățământ municipal școala Gimnazială Nr.2

Artă. Grigoropolisskaya, 2018

Introducere________________________________________________________________3-4p.

Capitolul 1. Istoria apariției fractalilor.___________________________________5-6pp.

Capitolul 2. Clasificarea fractalilor.________________________________________________6-10pp.

Fractali geometrici

Fractali algebrici

Fractali stocastici

Capitolul 3. „Geometria fractală a naturii”_________________________________11-13pp.

Capitolul 4. Aplicarea fractalilor________________________________________________13-15pp.

Capitolul 5 Lucrări practice________________________________________________16-24pp.

Concluzie________________________________________________________________25.pag

Lista referințelor și resurselor de pe Internet_________________________________________26 pagini.

Introducere

Când este privită corect, matematica reflectă nu numai adevărul, ci și frumusețea incomparabilă.

Bertrand Russell

În munca mea, am decis să „ating” lumea frumuseții și m-am hotărât pentru mine...

Scopul lucrării: crearea de obiecte ale căror imagini sunt foarte asemănătoare cu cele naturale.

Metode de cercetare: analiză comparativă, sinteză, modelare.

Sarcini:

cunoașterea conceptului, istoria originii și cercetările lui B. Mandelbrot, G. Koch, W. Sierpinski și alții;

cunoașterea diferitelor tipuri de mulțimi fractale;

studierea literaturii științifice populare pe această problemă, familiarizarea cu

ipoteze științifice;

găsirea confirmării teoriei fractalității lumii înconjurătoare;

studierea utilizării fractalilor în alte științe și în practică;

efectuarea unui experiment pentru a crea propriile imagini fractale.

Întrebarea fundamentală a lucrării:

Pentru a arăta că matematica nu este un subiect sec, fără suflet; ea poate exprima lumea spirituală a unei persoane în mod individual și în societate în ansamblu.

Subiect de studiu: Geometrie fractală.

Obiect de studiu: fractali în matematică și în lumea reală.

Ipoteză: Tot ceea ce există în lumea reală este un fractal.

Metode de cercetare: analitic, căutare.

Relevanţă Tema enunțată este determinată, în primul rând, de subiectul cercetării, care este geometria fractală.

Rezultatul muncii va fi crearea unei prezentări pe computer, a unui buletin informativ și a unei broșuri.

Capitolul 1. Istorie

B când un Mandelbrot

Conceptul de „fractal” a fost inventat de Benoit Mandelbrot. Cuvântul provine din latinescul „fractus”, care înseamnă „rupt, rupt”.

Practic, fractalii sunt clasificați în trei grupe:

Fractali algebrici

Fractali stocastici

Fractali geometrici

Să aruncăm o privire mai atentă la fiecare dintre ele.

Capitolul 2. Clasificarea fractalilor. Fractali geometrici

Cercetătorul M. Brown a schițat traiectoria de mișcare a particulelor în suspensie în apă și a explicat acest fenomen după cum urmează: atomii în mișcare aleatoriu ai lichidului lovesc particulele suspendate și, prin urmare, le pun în mișcare. După această explicație a mișcării browniene, oamenii de știință s-au confruntat cu sarcina de a găsi o curbă care să arate cel mai bine mișcarea particulelor browniene. Pentru a face acest lucru, curba trebuia să îndeplinească următoarele proprietăți: să nu aibă tangentă în niciun punct. Matematicianul Koch a propus o astfel de curbă.

LA Curba Koch este un fractal geometric tipic. Procesul de construire este următorul: luăm un singur segment, îl împărțim în trei părți egale și înlocuim intervalul din mijloc cu un triunghi echilateral fără acest segment. Ca rezultat, se formează o linie întreruptă, constând din patru verigi cu lungimea de 1/3. În pasul următor, repetăm operația pentru fiecare dintre cele patru legături rezultate etc...

Curba limită este curba Koch.

Fulgul de nea Koch. Efectuând o transformare similară pe laturile unui triunghi echilateral, puteți obține o imagine fractală a unui fulg de zăpadă Koch.

T
Un alt reprezentant simplu al unui fractal geometric este Piața Sierpinski. Este construit destul de simplu: pătratul este împărțit prin linii drepte paralele cu laturile sale în 9 pătrate egale. Pătratul central este eliminat din pătrat. Rezultatul este un set format din cele 8 pătrate rămase de „primul rang”. Făcând exact același lucru cu fiecare dintre pătratele de rangul întâi, obținem un set format din 64 de pătrate de rangul doi. Continuând acest proces la nesfârșit, obținem o succesiune infinită sau pătrat Sierpinski.

Fractali algebrici

E Acesta este cel mai mare grup de fractali. Fractalii algebrici își primesc numele deoarece sunt construiți folosind formule algebrice simple.

ÎN Ca exemplu, luați în considerare mulțimea Mandelbrot. Ei îl construiesc folosind numere complexe.

O secțiune a graniței mulțimii Mandelbrot, mărită de 200 de ori.

P

Un exemplu de alt fractal algebric este mulțimea Julia.Există 2 varietăți ale acestui fractal.În mod surprinzător, mulțimile Julia sunt formate folosind aceeași formulă ca și mulțimea Mandelbrot. Setul Julia a fost inventat de matematicianul francez Gaston Julia, după care a fost numit setul.

ȘI
fapt interesant , unii fractali algebrici seamănă izbitor cu imagini de animale, plante și alte obiecte biologice, drept urmare sunt numiți biomorfi.

Fractali stocastici

Un reprezentant tipic al acestui grup de fractali este „plasma”.

D

Pentru a-l construi, luați un dreptunghi și atribuiți o culoare fiecărui colț. Apoi, punctul central al dreptunghiului este găsit și pictat cu o culoare egală cu media aritmetică a culorilor de la colțurile dreptunghiului plus un număr aleatoriu. Cu cât numărul aleatoriu este mai mare, cu atât desenul va fi mai „zdrențuit”.Dacă ne uităm la acest fractal în secțiune transversală, vom vedea că acest fractal este tridimensional și are o „rugozitate”, tocmai din cauza acestei „rugozi” există o aplicație foarte importantă a acestui fractal.

Acum să vorbim despre fractali geometrici..

Capitolul 3 „Geometria fractală a naturii”

„De ce geometria este adesea numită „rece” și „uscă”? Un motiv este incapacitatea ei de a descrie forma unui nor, munte, coastă sau copac.” (Benoit Mandelbrot „Geometria fractală a naturii” ).

LA Frumusețea fractalilor este dublă: încântă ochiul, așa cum demonstrează expoziția mondială de imagini fractale, organizată de un grup de matematicieni din Bremen sub conducerea lui Peitgen și Richter. Mai târziu, exponatele acestei expoziții grandioase au fost surprinse în ilustrații pentru cartea acelorași autori, „Frumusețea fractalilor”.

Natura creează adesea fractali uimitori și frumoși, cu o geometrie ideală și o astfel de armonie încât pur și simplu îngheți de admirație. Și iată exemplele lor:

Scoici

Fulger admira cu frumusetea lor. Fractalii creați de fulgere nu sunt arbitrari sau regulați

Forma fractală subspecie de conopidă(Brassica cauliflora). Această specie particulară este un fractal deosebit de simetric.

P ferigă este, de asemenea, un bun exemplu de fractal printre floră.

Păuni toată lumea este cunoscută pentru penajul lor colorat, în care sunt ascunse fractali solide.

Gheață, modele geroase pe ferestre acestea sunt tot fractali

DESPRE
t imagine mărită frunze, inainte de ramuri de copac- fractalii pot fi găsiți în orice

Capitolul 4. Aplicarea fractalilor

DESPRE
zilele celor mai puternice aplicații ale fractalilor se află grafica pe computer. Aceasta este compresia imaginii fractale.

T
Geometria fractală este, de asemenea, folosită pentru proiectarea dispozitivelor de antenă. Acesta a fost folosit pentru prima dată de inginerul american Nathan Cohen, care locuia atunci în centrul Bostonului, unde era interzisă instalarea de antene externe pe clădiri. Există, de asemenea, multe ipoteze despre utilizarea fractalilor - de exemplu, sistemele limfatic și circulator, plămânii și multe altele au și proprietăți fractale.

Capitolul 5. Lucrări practice.

Mai întâi, să ne uităm la fractalii „Colier”, „Victorie” și „Pătrat”.

Fractal „Trandafir” (Fig. 10), datorită asemănării sale externe cu această floare. În fiecare cerc este înscris un hexagon regulat, a cărui latură este egală cu raza cercului circumscris în jurul lui.

Experimentul nr. 1 „Arborele”

Acum că am înțeles ce este un fractal și cum să construiesc unul, am încercat să-mi creez propriile imagini fractale.

Pentru început, am creat un fundal pentru viitorul nostru fractal cu o rezoluție de 600 x 600. Apoi am desenat 3 linii pe acest fundal - baza viitorului nostru fractal.

Deci, am un fractal cu drepturi depline! La baza acestui fractal se află primele trei linii pe care le-am menționat la începutul lucrării de cercetare.

Proprietatea fractală este mini-pomul de Crăciun pe părțile laterale ale bradului principal de Crăciun, brazii mici de Crăciun au, de asemenea, proprii lor brazi de Crăciun și așa mai departe la infinit. De data aceasta vom trasa linii arbitrare - baza viitorului nostru fractal.

P
După mai multe repetări obții un brad atât de drăguț!

Experimentul nr. 2

P
construirea de fractali folosind metoda recursiunii în mediul PascalABC.

Arborele lui Pitagora este un tip de fractal bazat pe figura cunoscută sub numele de Pantaloni Pitagoreici. Dacă în arborele pitagoreic clasic unghiul este de 45 de grade, atunci este și posibil să construiți un arbore pitagoreic generalizat folosind alte unghiuri. Acest copac este adesea numit arborele suflat de vânt al lui Pitagora.

Dacă înfățișați doar segmente care conectează într-un fel „centrele” triunghiurilor selectate, obțineți un copac pitagoreic gol. Combinând procedurile descrise mai sus într-un singur program, am primit un peisaj fractal.

Concluzie

Această lucrare este o introducere în lumea fractalilor. Am luat în considerare doar cea mai mică parte din ceea ce sunt fractalii și pe baza ce principii sunt construite.

Grafica fractală nu este doar un set de imagini care se repetă automat, este un model al structurii și principiului oricărui lucru existent. Întreaga noastră viață este reprezentată de fractali. Toată natura din jurul nostru este formată din ele. Este imposibil să nu remarcăm utilizarea pe scară largă a fractalilor în jocurile pe calculator; cu ajutorul fractalilor sunt create multe efecte speciale, diverse imagini fabuloase și incredibile etc. De asemenea, copacii, norii, țărmurile și toate celelalte naturi sunt desenate folosind geometria fractală. Grafica fractală este necesară peste tot, iar dezvoltarea „tehnologiilor fractale” este una dintre sarcinile importante astăzi.

1. Comprimarea imaginilor și a informațiilor

2. Ascunderea informațiilor din imagine, sunet,...

3. Criptarea datelor folosind algoritmi fractali

4. Realizarea muzicii fractale

5. Modelarea sistemului

Lucrarea mea nu enumeră toate domeniile cunoașterii umane în care teoria fractalilor și-a găsit aplicația. Vreau doar să spun că nu a trecut mai mult de o treime de secol de când a apărut teoria, dar în acest timp fractalii pentru mulți cercetători au devenit o lumină strălucitoare bruscă în noapte, care a iluminat fapte și modele necunoscute până acum în anumite zone de date. . Cu ajutorul teoriei fractalilor, au început să explice evoluția galaxiilor și dezvoltarea celulelor, apariția munților și formarea norilor. În pregătirea acestei lucrări, a fost foarte interesant pentru noi să găsim aplicații ale TEORIEI în PRACTICĂ. Pentru că de foarte multe ori există sentimentul că cunoștințele teoretice se deosebesc de realitatea vieții.

Știința fractală este încă foarte tânără și are un viitor mare în față. Frumusețea fractalilor este departe de a fi epuizată și încă ne va oferi multe capodopere - cele care încântă ochiul și cele care aduc adevărată plăcere minții.

10. Referințe

Bozhokin S.V., Parshin D.A. Fractali și multifractali. RHD 2001 .

Vitolin D. Aplicarea fractalilor în grafica computerizată. // Computerworld-Rusia.-1995

Mandelbrot B. Seturi de fractali autoafine, „Fractali în fizică”. M.: Mir 1988

Mandelbrot B. Geometria fractală a naturii. - M.: „Institutul de Cercetări Informatice”, 2002.

Morozov A.D. Introducere în teoria fractalilor. N. Novgorod: Editura Nijni Novgorod. Universitatea 1999

Peitgen H.-O., Richter P. H. Frumusețea fractalilor. - M.: „Mir”, 1993.

Resurse de internet

http://www.ghcube.com/fractals/determin.html

http://fractals.nsu.ru/fractals.chat.ru/

http://fractals.nsu.ru/animations.htm

http://www.cootey.com/fractals/index.html

http://fraktals.ucoz.ru/publ

http://sakva.narod.ru

http://rusnauka.narod.ru/lib/author/kosinov_n/12/

http://www.cnam.fr/fractals/

http://www.softlab.ntua.gr/mandel/

http://subscribe.ru/archive/job.education.maths/201005/06210524.html

Aplicație

orez. 7.Fractal „Colier” Fig.8. Fractal „Victorie”

Fig. 9. Fractal „Pătrat” Fig. 10. Fractal „Trandafir”

Orez. 12. Fractal „Pentagramă” fractal „Gaura Neagră”

Ministerul Educației și Științei al Republicii Kazahstan

Universitatea Tehnică de Stat Karaganda

Departamentul ______CAD______

NOTĂ EXPLICATIVĂ

pentru munca de curs

Disciplina: „Teoria sistemelor aplicate”

Subiect: „Fractali”

Supraveghetor

Ramurile tuburilor traheale, frunzele copacilor, venele în mână, un râu care clocotește și se îndoaie, bursa - toate acestea sunt fractali. De la civilizațiile antice până la Michael Jackson, oamenii de știință, matematicienii și artiștii, ca toți ceilalți de pe această planetă, au fost fascinați de fractali și i-au folosit în munca lor.

Programatorii și informaticienii sunt, de asemenea, înnebuniți după fractali, deoarece fractalii de complexitate și frumusețe infinite pot fi generați prin formule simple pe computere simple de acasă. Descoperirea fractalilor a fost descoperirea unei noi estetici în artă, știință și matematică, precum și o revoluție în percepția umană asupra lumii.

2. Partea teoretică

2.1 Conceptul de „fractal”

Conceptele de geometrie fractală și fractală, care au apărut la sfârșitul anilor '70, au devenit ferm stabilite în rândul matematicienilor și programatorilor încă de la mijlocul anilor '80. Cuvântul fractal este derivat din latinescul fractus și înseamnă format din fragmente. A fost propus de Benoit Mandelbrot în 1975 pentru a se referi la structurile neregulate, dar auto-asemănătoare de care era preocupat. Nașterea geometriei fractale este de obicei asociată cu publicarea cărții lui Mandelbrot „Geometria fractală a naturii” în 1977. Lucrările sale au folosit rezultatele științifice ale altor oameni de știință care au lucrat în perioada 1875-1925 în același domeniu (Poincaré, Fatou, Julia, Cantor, Hausdorff). Dar numai în vremea noastră a fost posibilă combinarea muncii lor într-un singur sistem.

Rolul fractalilor în grafica computerizată astăzi este destul de mare. Aceștia vin în ajutor, de exemplu, atunci când este necesar, folosind mai mulți coeficienți, să definească linii și suprafețe de forme foarte complexe. Din punctul de vedere al graficii pe computer, geometria fractală este indispensabilă atunci când se generează nori artificiali, munți și suprafețe maritime. De fapt, s-a găsit o modalitate de a reprezenta cu ușurință obiecte complexe non-euclidiene, ale căror imagini sunt foarte asemănătoare cu cele naturale.

Una dintre principalele proprietăți ale fractalilor este auto-asemănarea. În cel mai simplu caz, o mică parte a unui fractal conține informații despre întregul fractal.

2.2 Aplicarea fractalilor

Sisteme informatice.

Cea mai utilă utilizare a fractalilor în informatică este compresia datelor fractale. Acest tip de compresie se bazează pe faptul că lumea reală este bine descrisă de geometria fractală. În același timp, imaginile sunt comprimate mult mai bine decât se face cu metodele convenționale (cum ar fi jpeg sau gif). Un alt avantaj al compresiei fractale este că atunci când imaginea este mărită, nu există nici un efect de pixelare (mărește dimensiunea punctelor până la dimensiuni care distorsionează imaginea). Cu compresia fractală, după mărire, imaginea arată adesea chiar mai bine decât înainte.

Mecanica fluidelor.

Studiul turbulenței în fluxuri se adaptează foarte bine la fractali. Fluxurile turbulente sunt haotice și, prin urmare, dificil de modelat cu acuratețe. Și aici tranziția la o reprezentare fractală ajută, ceea ce facilitează foarte mult munca inginerilor și fizicienilor, permițându-le să înțeleagă mai bine dinamica complexului.

Folosind fractali puteți simula și flăcări.

Materialele poroase sunt bine reprezentate sub formă fractală datorită faptului că au o geometrie foarte complexă. Este folosit în știința petrolului.

Telecomunicatii.

Pentru a transmite date la distanțe, se folosesc antene cu forme fractale, ceea ce le reduce foarte mult dimensiunea și greutatea.

Fizica suprafetelor.

Fractalii sunt folosiți pentru a descrie curbura suprafețelor. O suprafață neuniformă este caracterizată de o combinație de doi fractali diferiți.

Medicament.

1. Interacțiuni biosenzoriale

2. Bătăile inimii

Biologie.

Modelarea proceselor haotice, în special atunci când se descriu modele de populație.

2.3 Teoria haosului

Teoria haosului este studiul sistemelor dinamice neliniare complexe. Adevărata stare de lucruri este discutată mai jos ca răspuns la multe concepții greșite despre acest domeniu al științei.

2.3.1 Introducere în teoria haosului

Ce este teoria haosului?

Formal, teoria haosului este definită ca studiul sistemelor dinamice neliniare complexe. Aceasta este ceea ce se înțelege prin termenul complex, iar prin termenul neliniar înțelegem recursivitate și algoritmi din matematica superioară, iar, în sfârșit, dinamic înseamnă non-constant și neperiodic. Astfel, teoria haosului este studiul sistemelor complexe în continuă schimbare, bazate pe concepte non-matematice de recursivitate, fie sub forma unui proces recursiv sau a unui set de ecuații diferențiale care modelează un sistem fizic.

2.3.2 Teoria haosului despre dezordine

Cea mai frecventă discrepanță este că oamenii cred că teoria haosului este o teorie despre dezordine. Nimic mai departe de adevăr! Aceasta nu este o respingere a determinismului sau o afirmație că sistemele ordonate sunt imposibile; aceasta nu este o negare a dovezilor experimentale sau o afirmație că sistemele complexe sunt inutile. Haosul în teoria haosului este ordine - și nici măcar ordine, ci esența ordinii.

Este adevărat că teoria haosului afirmă că micile schimbări pot produce consecințe uriașe. Dar unul dintre conceptele centrale ale teoriei este imposibilitatea de a prezice cu exactitate starea unui sistem. În general, sarcina de a modela comportamentul general al unui sistem este destul de fezabilă, chiar simplă. Astfel, teoria haosului își concentrează eforturile nu pe dezordinea sistemului - imprevizibilitatea ereditară a sistemului - ci pe ordinea pe care a moștenit-o - comportamentul comun al sistemelor similare.

Astfel, ar fi incorect să spunem că teoria haosului este despre dezordine. Pentru a ilustra acest lucru cu un exemplu, să luăm atractorul Lorentz. Se bazează pe trei ecuații diferențiale, trei constante și trei condiții inițiale.

Figura 1. Atractor Lorentz.

Un atractor reprezintă comportamentul unui gaz la un moment dat, iar starea lui la un moment dat depinde de starea sa din momentele care preced acel moment. Dacă datele originale sunt modificate chiar și cu cantități foarte mici, să spunem că aceste valori sunt suficient de mici pentru a fi comparabile cu contribuția atomilor individuali la numărul lui Avogadro (care este un număr foarte mic în comparație cu valorile de ordinul 1024), verificarea stării atractorului va arăta numere complet diferite. Acest lucru se întâmplă deoarece micile diferențe sunt mărite prin recursivitate.

Cu toate acestea, în ciuda acestui fapt, graficul atractor va arăta destul de asemănător. Ambele sisteme vor avea valori complet diferite la un moment dat, dar graficul atractor va rămâne același deoarece exprimă comportamentul general al sistemului.

Teoria haosului spune că sistemele neliniare complexe sunt în mod inerent imprevizibile, dar, în același timp, teoria haosului spune că modalitatea de a exprima astfel de sisteme imprevizibile se dovedește a fi corectă nu în egalități exacte, ci în reprezentări ale comportamentului sistemului - în grafice atractoare ciudate. sau în fractali. Astfel, teoria haosului, despre care mulți oameni o consideră impredictibilitate, se dovedește a fi, în același timp, știința predictibilității chiar și în cele mai instabile sisteme.

2.3.3 Aplicarea teoriei haosului în lumea reală

Când apar teorii noi, toată lumea vrea să știe ce este bun la ele. Deci, ce este bun la teoria haosului?

În primul rând și cel mai important, teoria haosului este o teorie. Aceasta înseamnă că cea mai mare parte este folosită mai mult ca bază științifică decât ca cunoștințe direct aplicabile. Teoria haosului este o modalitate foarte bună de a privi evenimentele care au loc în lume diferit de viziunea mai tradițională clar deterministă care a dominat știința de la Newton. Spectatorii care au văzut Jurassic Park se tem, fără îndoială, că teoria haosului poate influența foarte mult percepția umană asupra lumii și, de fapt, teoria haosului este utilă ca mijloc de interpretare a datelor științifice în moduri noi. În loc de diagramele X-Y tradiționale, oamenii de știință pot interpreta acum diagramele faze-spațiu care - în loc să descrie poziția exactă a oricărei variabile într-un anumit moment în timp - reprezintă comportamentul general al unui sistem. În loc să ne uităm la egalități exacte bazate pe date statistice, putem acum să ne uităm la sisteme dinamice cu un comportament similar în natură cu datele statice - de exemplu. sisteme cu atractori similari. Teoria haosului oferă un cadru puternic pentru dezvoltarea cunoștințelor științifice.

Cu toate acestea, conform celor de mai sus, nu rezultă că teoria haosului nu are aplicații în viața reală.

Tehnicile teoriei haosului au fost folosite pentru modelarea sistemelor biologice, care sunt, fără îndoială, unele dintre cele mai haotice sisteme imaginabile. Sistemele de ecuații dinamice au fost folosite pentru a modela totul, de la creșterea populației și epidemii până la bătăi aritmice ale inimii.

În realitate, aproape orice sistem haotic poate fi modelat - bursa produce curbe care pot fi ușor analizate folosind atractori ciudați, spre deosebire de relații exacte; procesul picăturilor care cad dintr-un robinet care curge pare aleatoriu atunci când este analizat de urechea goală, dar atunci când este reprezentat ca un atractor ciudat, dezvăluie o ordine ciudată care nu ar fi așteptată de la mijloacele tradiționale.

Fractalii sunt peste tot, cel mai proeminent în programele de grafică, cum ar fi seria de produse de mare succes Fractal Design Painter. Tehnicile de compresie a datelor fractale sunt încă în curs de dezvoltare, dar promit rezultate uimitoare, cum ar fi un raport de compresie de 600:

1. Industria filmelor de efecte speciale ar avea elemente de peisaj mult mai puțin realiste (nori, roci și umbre) fără tehnologia grafică fractală.

Și, desigur, teoria haosului oferă oamenilor o modalitate surprinzător de interesantă de a câștiga interes pentru matematică, una dintre cele mai puțin populare domenii de cunoaștere în prezent.

2.3.4 Mișcarea browniană și aplicațiile acesteia

Mișcarea browniană este, de exemplu, mișcarea aleatorie și haotică a particulelor de praf suspendate în apă. Acest tip de mișcare este poate aspectul geometriei fractale care are cea mai practică utilizare. Mișcarea aleatorie browniană produce un model de frecvență care poate fi folosit pentru a prezice lucruri care implică cantități mari de date și statistici. Un bun exemplu este prețul lânii, pe care Mandelbrot l-a prezis folosind mișcarea browniană.

Figura 2. Diagrama de frecvență.

Diagramele de frecvență create prin trasarea numerelor browniene pot fi, de asemenea, convertite în muzică. Desigur, acest tip de muzică fractală nu este deloc muzicală și poate plictisi cu adevărat ascultătorul. Prin trasarea aleatorie a numerelor browniene pe un grafic, puteți obține un Fractal de praf ca cel prezentat aici ca exemplu.

Pe lângă utilizarea mișcării browniene pentru a produce fractali din fractali, poate fi folosit și pentru a crea peisaje. Multe filme științifico-fantastice, cum ar fi Star Trek, au folosit tehnica mișcării browniene pentru a crea peisaje extraterestre, cum ar fi dealurile și modelele topologice ale platourilor montane înalte. Aceste tehnici sunt foarte eficiente și pot fi găsite în cartea lui Mandelbrot The Fractal Geometry of Nature. Mandelbrot a folosit linii browniene pentru a crea linii de coastă fractale și hărți ale insulelor (care erau de fapt doar puncte desenate aleatoriu) dintr-o vedere de ochi de pasăre.

Figura 3. Relief.

2.4 Integrarea fractalilor determiniști și a haosului

Din exemplele de fractali determiniști discutate mai sus, puteți vedea că aceștia nu prezintă niciun comportament haotic și că sunt de fapt foarte previzibili. După cum știți, teoria haosului folosește un fractal pentru a recrea sau a găsi modele pentru a prezice comportamentul multor sisteme din natură, cum ar fi, de exemplu, problema migrației păsărilor.

Acum să vedem cum se întâmplă de fapt asta. Folosind un fractal numit Arborele lui Pitagora, care nu este discutat aici (care, de altfel, nu a fost inventat de Pitagora și nu are nimic de-a face cu teorema lui Pitagora) și mișcarea browniană (care este haotică), să încercăm să facem o imitație a unui copac adevărat. Ordonarea frunzelor și ramurilor pe un copac este destul de complexă și aleatorie și probabil nu este ceva suficient de simplu pe care să îl poată emula un program scurt de 12 linii.

Mai întâi trebuie să generați un Arbore Pitagore (Figura 4). Rezultatul amintește de acele desene vechi de grădiniță... Așa că haideți să facem cufărul mai gros. În această etapă, mișcarea browniană nu este utilizată. În schimb, fiecare segment de linie a devenit acum o linie de simetrie între dreptunghiul care devine trunchi și ramurile din exterior.

Figura 4. Arborele lui Pitagora

Dar rezultatul pare încă prea formal și ordonat. Copacul nu pare să fie încă viu. Să încercăm să aplicăm unele dintre cunoștințele în domeniul fractalilor determiniști pe care tocmai le-am dobândit.

Figura 5.

Acum puteți folosi mișcarea browniană pentru a crea un haos aleatoriu care schimbă numerele rotunjind-le la două cifre. Originalul folosea numere zecimale de 39 de biți. Rezultatul (stânga) nu arată ca un copac. În schimb, arată ca un cârlig inteligent!

Figura 6.

Poate că rotunjirea la 2 cifre a fost prea mult? Aplicăm din nou mișcarea browniană, de data aceasta rotunjită la 7 cifre. Rezultatul încă arată ca un cârlig, dar de data aceasta sub forma unei spirale logaritmice!

Figura 7.

Deoarece partea stângă (conținând toate numerele impare) nu produce un efect de cârlig, neregulile aleatorii produse de mișcarea browniană sunt aplicate de două ori tuturor numerelor din partea stângă și o singură dată numerelor din dreapta. Poate că acest lucru va fi suficient pentru a elimina sau reduce efectul spiralei logaritmice. Deci, numerele sunt rotunjite la 24 de cifre. De data aceasta, rezultatul este o emulare haotică computerizată cu aspect frumos a unui copac adevărat.

Figura 8.

2.5 Tipuri de fractali

zăbrele Sierpinski.

Acesta este unul dintre fractalii cu care Mandelbrot a experimentat atunci când a dezvoltat conceptele de dimensiuni și iterații fractale. Triunghiurile formate prin conectarea punctelor medii ale unui triunghi mai mare sunt tăiate din triunghiul principal, formând un triunghi cu mai multe găuri. În acest caz, inițiatorul este triunghiul mare, iar șablonul este operația de tăiere a triunghiurilor similare cu cel mai mare. De asemenea, puteți obține o versiune tridimensională a unui triunghi folosind un tetraedru obișnuit și tăind tetraedre mici. Dimensiunea unui astfel de fractal este ln3/ln2 = 1,584962501.

Pentru a obține un covor Sierpinski, luați un pătrat, împărțiți-l în nouă pătrate și decupați-l pe cel din mijloc. La fel vom face și cu restul, pătrate mai mici. În cele din urmă, se formează o rețea fractală plată, fără zonă, dar cu conexiuni infinite. În forma sa spațială, buretele Sierpinski este transformat într-un sistem de forme end-to-end, în care fiecare element end-to-end este înlocuit constant cu propriul său fel. Această structură este foarte asemănătoare cu o secțiune de țesut osos. Într-o zi, astfel de structuri care se repetă vor deveni un element al structurilor de construcție. Statica și dinamica lor, crede Mandelbrot, merită studiate îndeaproape.

Figura 9. Rețeaua Sierpinski.

Figura 10. Buretele Sierpinski.

triunghiul Sierpinski.

Nu confundați acest fractal cu rețeaua Sierpinski. Acestea sunt două obiecte complet diferite. În acest fractal, inițiatorul și generatorul sunt la fel. La fiecare iterație, o copie mai mică a inițiatorului este adăugată în fiecare colț al generatorului și așa mai departe. Dacă s-ar efectua un număr infinit de iterații la crearea acestui fractal, acesta ar ocupa întregul plan, fără a lăsa o singură gaură. Prin urmare, dimensiunea sa fractală este ln9/ln3 = 2,0.

Figura 11. Triunghiul Sierpinski.

curba Koch.

Curba Koch este unul dintre cei mai tipici fractali determiniști. A fost inventat în secolul al XIX-lea de un matematician german pe nume Helge von Koch, care, în timp ce studia lucrările lui Georg Kontor și Karl Weierstrasse, a dat peste descrieri ale unor curbe ciudate cu un comportament neobișnuit. Inițiatorul este o linie dreaptă. Generatorul este un triunghi echilateral, ale cărui laturi sunt egale cu o treime din lungimea segmentului mai mare. Aceste triunghiuri sunt adăugate la mijlocul fiecărui segment din nou și din nou. În cercetările sale, Mandelbrot a experimentat intens cu curbele Koch și a produs figuri precum Insulele Koch, Crucile Koch, Fulgii de zăpadă Koch și chiar reprezentări tridimensionale ale curbei Koch, folosind un tetraedru și adăugând tetraedre mai mici la fiecare dintre fețele sale. Curba Koch are dimensiunea ln4/ln3 = 1,261859507.

Figura 12. Curba Koch.

Fractal Mandelbrot.

Acesta NU este setul Mandelbrot, pe care îl vedeți destul de des. Mulțimea Mandelbrot se bazează pe ecuații neliniare și este un fractal complex. Aceasta este, de asemenea, o variantă a curbei Koch, deși acest obiect nu este similar cu acesta. Inițiatorul și generatorul sunt, de asemenea, diferite de cele folosite pentru a crea fractali bazați pe principiul curbei Koch, dar ideea rămâne aceeași. În loc să unească triunghiuri echilaterale cu un segment de curbă, pătratele sunt unite cu un pătrat. Datorită faptului că acest fractal ocupă exact jumătate din spațiul alocat la fiecare iterație, are o dimensiune fractală simplă de 3/2 = 1,5

Figura 13. Fractal Mandelbrot.

Curba Dragonului.

Inventat de matematicianul italian Giuseppe Peano, Dragon Curve, sau Dragon Sweep, așa cum o numea el, este foarte asemănătoare cu un cârnați Minkowski. A fost folosit un inițiator mai simplu, iar generatorul a fost același. Mandelbrot a numit acest fractal Râul Double Dragon. Dimensiunea sa fractală este de aproximativ 1,5236.

Figura 14. Dragon de Giuseppe Peano.

Set Mandelbrot.

Seturile Mandelbrot și Julia sunt probabil cele mai comune dintre fractalii complecși. Acestea pot fi găsite în multe reviste științifice, coperți de cărți, cărți poștale și economizor de ecran de computer. Setul Mandelbrot, care a fost construit de Benoit Mandelbrot, este probabil prima asociere pe care oamenii o au atunci când aud cuvântul fractal. Acest fractal, care seamănă cu o mașină de cardare cu zone circulare și asemănătoare copacului în flăcări atașate la el, este generat printr-o formulă simplă

Zn+1=Zna+C, unde Z și C sunt numere complexe și a este un număr pozitiv.

Mulțimea Mandelbrot, care poate fi văzută cel mai adesea, este mulțimea Mandelbrot de gradul 2, adică a = 2. Faptul că mulțimea Mandelbrot nu este doar Zn+1=ZnІ+C, ci un fractal, al cărui indicator în formula poate fi orice număr pozitiv, i-a indus în eroare pe mulți. Pe această pagină vedeți un exemplu de set Mandelbrot pentru diferite valori ale exponentului a.

Procesul Z=Z*tg (Z+C) este de asemenea popular. Prin includerea funcției tangente, rezultatul este un set Mandelbrot înconjurat de o zonă asemănătoare unui măr. Când se utilizează funcția cosinus, se obțin efecte de bule de aer. Pe scurt, există un număr infinit de moduri de a configura setul Mandelbrot pentru a produce diferite imagini frumoase.

Figura 15. Mulțimea Mandelbrot.

Figura 16. Mandelbrot stabilit la a=3,5.

Multă Julia.

În mod surprinzător, mulțimile Julia sunt formate folosind aceeași formulă ca și mulțimea Mandelbrot. Setul Julia a fost inventat de matematicianul francez Gaston Julia, după care a fost numit setul. Prima întrebare care apare după o cunoaștere vizuală cu mulțimile Mandelbrot și Julia este „dacă ambii fractali sunt generați după aceeași formulă, de ce sunt atât de diferiți? „Uită-te mai întâi la pozele cu setul Julia. Destul de ciudat, există diferite tipuri de seturi Julia. Când desenați un fractal folosind diferite puncte de plecare (pentru a începe procesul de iterație), sunt generate imagini diferite. Acest lucru se aplică numai setului Julia.

Deși nu poate fi văzut în imagine, un fractal Mandelbrot este de fapt mulți fractali Julia conectați împreună. Fiecare punct (sau coordonată) al mulțimii Mandelbrot corespunde unui fractal Julia. Seturile Julia pot fi generate folosind aceste puncte ca valori inițiale în ecuația Z=ZI+C. Dar acest lucru nu înseamnă că, dacă selectați un punct pe fractalul Mandelbrot și îl măriți, puteți obține un fractal Julia. Aceste două puncte sunt identice, dar numai în sens matematic. Dacă luați acest punct și îl calculați folosind această formulă, puteți obține un fractal Julia corespunzător unui anumit punct al fractalului Mandelbrot.

Figura 17. Setul Julia.

Arborele Feigenbaum.

Ecuația logistică este formula la care Mitchell Feigenbaum a lucrat în primul rând pentru a-și crea teoria fractalilor. Această formulă ar trebui să descrie dinamica dezvoltării populației:

f (x) = (1 - x) rx

Cel mai simplu model este un raport proporțional al numărului față de anul precedent. Să spunem că anul trecut am avut x animale. Ar trebui să fie animale rx anul acesta. Dar acest lucru nu funcționează în condiții reale. O corespondență mai bună cu realitatea se va obține dacă adăugăm un factor în funcție de potențialul pe care îl are populația de dezvoltare ulterioară și fie x coeficientul de completitudine, care variază de la 0 la 1. Apoi se adaugă factorul 1 - x, astfel încât teritoriul este aproape complet umplut, populația nu va crește peste limita superioară.

Extinderea expresiei logistice, obținem:

f (x) = ax - ax2

Formula folosită în programul LT Bifurcator pentru a explica esența fractalului Feigenbaum - (1 + r) x - rx2 nu este foarte diferită de formula dată mai sus. În principiu, pentru a studia teoria, s-ar putea folosi orice formulă, de exemplu, cea mai simplă dintre formulele de acest tip - xI - r. Singurele diferențe sunt diferențele în coordonatele ferestrelor din imagine și un aspect ușor diferit al imaginii.

Figura 18. Arborele Feigenbaum.

2.6 Arborele Feigenbaum și setul Mandelbrot

Dacă ați văzut vreodată formula de multiplicitate Mandelbrot z=z2 + x, este posibil să observați similitudinea dintre această formulă și cea mai simplă dintre formulele de construire a arborelui Feigenbaum x2 - r. Și într-adevăr este. Există asemănări. Dar copacul lui Feigenbaum crește în cealaltă direcție. Schimbați formula lui Feigenbaum la x2 + r și veți vedea asemănarea. Pentru setul Mandelbrot, trebuie să priviți de-a lungul axei orizontale, deoarece aceasta este singura poziție în care partea complexă a numărului Mandelbrot este zero. Veți vedea că corpul principal al figurii Mandelbrot este locul în care funcția din arborele Feigenbaum ia o singură valoare. Când are loc prima diviziune a liniei (bifurcația), apare un nou corp pe figura Mandelbrot etc. De asemenea, rețineți că atunci când fereastra principală este deschisă în copac, pe figura Mandelbrot apare un corp de copil.

Figura 19. Arborele Feigenbaum și mulțimea Mandelbrot.

3. Enunțarea problemei

Este necesar să se proiecteze și să dezvolte un produs software cu care să fie posibilă vizualizarea vizuală a imaginilor graficelor fractale. Programul ar trebui să vă permită să dezvăluiți esența unui fractal - auto-repetiție multiplă (a întregii imagini sau a unei anumite părți a acesteia). Interfața ar trebui să fie cât mai clară posibil. Viteza de lucru ar trebui să fie astfel încât să echilibreze productivitatea și calitatea, de ex. cu această viteză se desenează o imagine destul de clară. Abilitatea de a salva o imagine fractală este, de asemenea, necesară. Programul ar trebui să fie intuitiv și „nu respingător la prima vedere”. Programul ar trebui să fie capabil să deseneze cel puțin zece fractali algebrici și cel puțin doi geometrici.

Soluţie.

Soluția la această problemă este un produs software cu care puteți vizualiza mai multe mostre de grafică fractală algebrică și geometrică. Programul trebuie să aibă încorporat o mărire (multiple) proporțională cu dimensiunea reală a imaginii. Interfața trebuie să fie luminoasă și plăcută, poate în tonurile WindowsXP. De exemplu, folosirea unui gradient de umplere pentru forma în sine este potrivită pentru noi. Având în vedere că oamenilor nu le plac așteptările lungi, programul nu folosește o dimensiune mare a pânzei, cu toate acestea, chiar și la această dimensiune este posibil să luăm în considerare toate avantajele graficii fractale. Programul folosește capabilități standard pentru salvarea imaginilor grafice în format *. bmp nu poate încărca imagini grafice cu acest format în sine, deoarece acest program nu este pentru vizualizare, ci pentru generarea de imagini. Programul folosește culori cerești, are o interfață ușor de utilizat și este ușor de utilizat. Fiecare buton, parametru și alte controale sunt etichetate astfel încât programul să nu aibă nevoie de ajutor, dar este totuși completat cu ajutor pentru a evita conflictele cu standardele. Capacitățile programului vă permit să desenați douăzeci și unu de fractali algebrici și trei geometrici.

Structura.

Programul constă din două formulare (cel principal și un formular cu numele dezvoltatorilor și logo-ul acestora). Formularul principal poate avea două interfețe:

Fractali algebrici

Fractali geometrici.

Există și o fereastră de ajutor.

Structura ulterioară a interfeței va fi descrisă în secțiunea „Ghidul utilizatorului”.

Structura programului este un set de funcții, fiecare dintre acestea fiind o „formulă” pentru desenarea unui fractal. Și procedurile de desen în sine.

Figura 20. Schema programului.

Această diagramă (Figura 20) arată principiul intern de funcționare al programului. Utilizarea unei singure proceduri de randare reduce semnificativ codul și dimensiunea componentelor interfeței. Cu toate acestea, reprezentarea fiecărei formule de set ca o funcție separată reduce semnificativ timpul de randare.

Manualul utilizatorului.

Pentru a instala acest produs software, trebuie să introduceți în unitate un disc cu o versiune licențiată a programului. Vrăjitorul de instalare va apărea pe ecran. Citind comentariile sale, puteți schimba locația fișierelor instalate. Dacă sunteți de acord cu adresele propuse de programul de instalare, faceți clic pe „următorul”. Apoi, pe desktop-ul computerului va apărea o pictogramă cu numele programului „Fractal Graphics”. Pentru a-l deschide, trebuie să treci mouse-ul peste el și să dai dublu clic pe el.

Acest program vă permite să vizualizați imagini cu douăzeci și unu de fractali algebrici și trei geometrici. Când pornim programul, acesta ne oferă automat o interfață de fractali algebrici. Pentru a trece la cele geometrice, trebuie să faceți clic pe butonul „Afișare” -> „Fractali geometrici” din bara de meniu.

Desenul are loc pe o zonă dreptunghiulară din jumătatea stângă a ferestrei programului numită pânză.

Meniul fractali algebrici are următoarele controale și intrări de parametri:

R - saturația culorii roșii

G - saturația culorii verde

B - saturația culorii albastre

Numărul de iterații este numărul de repetări ale coordonatelor unui punct atunci când se identifică apartenența acestuia la o anumită zonă (calitatea imaginii depinde de aceasta)

Lista posibilelor opțiuni fractale:

Desenare - buton de desen

Șterge - buton de ștergere

Implicit - valorile originale

Desenați timpul

Când lucrați cu fractali geometrici:

Sierpinski - desen al triunghiului Sierpinski, în dreapta parametrul este numărul de iterații

Dragon D. Piano - desen al dragonului D. Piano, parametrul din dreapta este numărul de iterații

Feigenbaum - desen al arborelui Feigenbaum, lista de parametri de mai jos

Clar - clar.

De asemenea, este posibil să salvați imaginea în format *. bmp. Pentru a face acest lucru, trebuie să desenați un fractal (mărește-l dacă doriți), apoi intrați în meniul - „Fișier” -> „Salvare”, fără a specifica extensia, introduceți numele fișierului și apăsați Enter.

Dacă trebuie să vizualizați structura fractală, trebuie să mutați cursorul mouse-ului peste o zonă a pânzei, faceți clic pe butonul din stânga, apoi întindeți zona necesară la dreapta și eliberați butonul mouse-ului.

Figura 21. Interfața programului.

Influența parametrilor.

La dezvoltarea acestui program s-au luat în considerare nu numai cerințele clientului, ci și unele cercetări au fost efectuate. Au fost identificate următoarele modele și fapte:

Pe măsură ce numărul de iterații crește, calitatea imaginii crește, dar crește și viteza de randare. De asemenea, atunci când mărim un fractal cu un număr mare de iterații, putem vedea mai multe imagini vizuale, iar posibilul factor de mărire crește considerabil.

Selectarea coeficienților de culoare este o muncă foarte complexă și minuțioasă, care necesită o mulțime de ore de muncă.

Timpul de desen depinde și de funcțiile selectate. Deci, funcțiile de putere sunt desenate mult mai rapid decât, de exemplu, funcțiile de putere.

În timpul lucrării, a fost creat un număr considerabil de fractali, dintre care cei mai buni au fost selectați prin inspecție vizuală. Formulele prin care sunt trase au fost derivate exclusiv de dezvoltatori și sunt proprietatea lor privată.

Valorile inițiale ale variabilelor din funcții pot schimba aspectul fractalului, astfel încât originalul său va fi vizual complet diferit de clonă. Acest principiu, de exemplu, a fost aplicat de Julia.

Raza cercului - standardul pe care sunt generate punctele - este cel mai important parametru. De exemplu, fractalii construiti pe baza setului Mandelbrot - Spider (i) diferă doar în această rază.

Coordonatele inițiale ale desenului determină caracterul complet al imaginii de pe pânză. Dacă sunt plasate incorect, fractalul poate să nu fie complet vizibil.

Mulți parametri afectează frumusețea unui fractal. La construirea acestuia, toți parametrii trebuie să fie calculati și gândiți cu precizie. Aceasta este cheia unei imagini de înaltă calitate.

Concluzie

Grafica fractală nu este doar un set de imagini care se repetă automat, este un model al structurii și principiului oricărui lucru existent. Întreaga noastră viață este reprezentată de fractali. Nu numai vizual, ci și structura acestei imagini reflectă viața noastră. Luați ADN-ul, de exemplu, este doar baza, o iterație, iar când se repetă... apare o persoană! Și există multe astfel de exemple. Este imposibil să nu remarcăm utilizarea pe scară largă a fractalilor în jocurile pe calculator, unde reliefurile de teren sunt adesea imagini fractale bazate pe modele tridimensionale de seturi complexe și mișcare browniană. Grafica fractală este necesară peste tot, iar dezvoltarea „tehnologiilor fractale” este una dintre sarcinile importante astăzi.

Vizualizări