Ecuație liniară cu o variabilă (gradul 7). plan de lecție de algebră (clasa a VII-a) pe tema. Rezolvarea ecuațiilor liniare cu o variabilă Formularea scopului și obiectivelor lecției

Plan de lecție pentru algebră în clasa a 7-a B.

Ecuație liniară cu o variabilă.

(04.10.2012)

Scopul lecției. Formarea abilității de a rezolva o ecuație cu o necunoscută, reducând-o la o ecuație liniară folosind proprietățile echivalenței.

Tipul de lecție: combinat.

Obiectivele lecției:

1) educațional:

Să familiarizeze elevii cu tipul de ecuație liniară și metoda de rezolvare a acesteia, să obțină stăpânirea regulii de rezolvare a ecuațiilor liniare, înțelegerea acesteia și capacitatea de a o folosi la rezolvare;

2) dezvoltarea:

continuă formarea cunoștințelor matematice și a tehnicilor de activitate mentală (capacitatea de a analiza o situație și de a naviga prin acțiuni, de a învăța să efectueze o nouă acțiune, de a o aduce la automatizare). Formează elemente de logică matematică.

3) educațional:

formarea deprinderii de a lucra pas cu pas sub îndrumarea unui profesor (explicarea noului material, consolidarea inițială), percepția informației după ureche (cartoașe), formarea stimei de sine (reflecție).

În timpul orelor

I. Verificarea frontală a temelor.

II. Lucrare orală (pe cartonașe)

Scopul muncii orale: diagnosticarea dezvoltării abilităților de rezolvare a ecuațiilor liniare cu o variabilă.

1. În loc de (*) pune semnul „+” sau „-”, iar în loc de puncte - numere:

a) (*5)+(*7)=2;

b) (*8)-(*8)=(*4)-12;

c) (*9)+(*4)=-5;

d) (-15)-(*…)=0;

e) (*8)+(*…)=-12;

e (*10)-(*…)=12.

2. Creați ecuații echivalente cu ecuația:

a) x-7=5;

b) 2x-4=0;

c) x-11=x-7;

d) 2(x-12)=2x-24.

III. Generalizarea capacității de a rezolva ecuații prin reducerea lor la o ecuație liniară.

Lucru în grup cu clasa.

Forma muncii colective: frontal

Să rezolvăm ecuația

12 - (4x-18)=(36+5x)+(28 – 6x). (1)

Pentru a face acest lucru, efectuăm următoarele transformări:

1. Să deschidem parantezele. Dacă parantezele sunt precedate de un semn plus, parantezele pot fi omise menținând semnul fiecărui termen cuprins între paranteze. Dacă parantezele sunt precedate de un semn minus, parantezele pot fi omise prin schimbarea semnului fiecărui termen cuprins între paranteze:

12 - 4x+18=36+5x+28 – 6x. (2)

Ecuațiile (2) și (1) sunt echivalente.

2. Să mutăm termenii necunoscuți cu semne opuse astfel încât să se afle într-o singură parte a ecuației (fie în stânga, fie în dreapta). În același timp, mutăm termenii cunoscuți cu semne opuse, astfel încât să fie doar în cealaltă parte a ecuației.

De exemplu, să transferăm termenii necunoscuți cu semne opuse la stânga, iar cei cunoscuți în partea dreaptă a ecuației, apoi obținem ecuația

4x-5x+6x=36+28-18, (3)

echivalent cu ecuația (2) și, prin urmare, cu ecuația (1).

3. Să prezentăm termeni similari:

3x=46. (4)

Ecuația (4) este echivalentă cu ecuația (3) și, prin urmare, cu ecuația (1).

4. Împărțiți ambele părți ale ecuației (4) la coeficientul necunoscutului. Ecuația rezultată x=46/-3 sau -15 1/3 va fi echivalentă cu ecuația (4) și, prin urmare, cu ecuațiile (3), (2), (1).

Prin urmare, rădăcina ecuației (1) va fi numărul -15 1/3.

Folosind această schemă (algoritm), rezolvăm ecuații în lecția de astăzi:

1. Deschideți parantezele.

2. Colectați termenii care conțin necunoscutele într-o parte a ecuației și termenii rămași în cealaltă.

3. Dați termeni similari.

4. Împărțiți ambele părți ale ecuației la coeficientul necunoscutului.

Notă: trebuie menționat că diagrama de mai sus nu este obligatorie, deoarece există adesea ecuații pentru care unii dintre pașii indicați nu sunt necesari pentru rezolvare. Când rezolvați alte ecuații, poate fi mai ușor să vă abateți de la această schemă, ca, de exemplu, în ecuația:

7(x-2)=42.

IV. Exerciții de antrenament.

№№ 132 (a, d), 133 (a, d), 136 (c), 138 (d) - cu o notă pe tablă.

№132. Aflați rădăcina ecuației:

a) (13x-15)-(9+6x)=-3x

Să extindem parantezele:

13x-15-9-6x=-3x.

Să transferăm termenii necunoscuți cu semne opuse la stânga, iar cei cunoscuți în partea dreaptă a ecuației, apoi obținem ecuația:

13x-6x+3x=15+9.

Să prezentăm termeni similari.

10x=24.

Să împărțim ambele părți ale ecuației la coeficientul necunoscutului.

x=2,4

Răspuns: 2.4

d) (0,5x+1,2)-(3,6-4,5x)=(4,8-0,3x)+(10,5x+0,6);

0,5x+1,2-3,6+4,5x=4,8-0,3x+10,5x+0,6;

0,5x+4,5x+0,3x-10,5x=4,8+0,6-1,2+3,6;

5,2x=7,8;

x=-1,5

Răspuns: -1,5

№133 Găsiți rădăcina ecuației:

a) 5(3x+1,2) + x = 6,8,

15x + 6 + x = 6,8,

15x + x = 6,8 – 6,

16x = 0,8,

x = 0,8: 16,

x = 0,05,

Răspuns: 0,05

d) 5,6 - 7y = - 4(2y – 0,9) + 2,4,

5,6 – 7y = - 8y + 3,6 + 2,4,

8y – 7y = 3,6 + 2,4 – 5,6,

y = 0,4,

Răspuns: 0,4

№ 136. Rezolvați ecuația:

c) 0,8x – (0,7x + 0,36) = 7,1,

0,8x – 0,7x – 0,36 = 7,1,

0,1x = 0,36 + 7,1,

0,1x = 7,46,

x = 7,46: 0,1,

x = 74,6

Răspuns: 74,6.

№ 138. Aflați rădăcina ecuației:

d) -3(y + 2,5) = 6,9 – 4,2y,

3y – 7,5 = 6,9 – 4,2y,

4,2y – 3y = 6,9 + 7,5,

1,2у = 14,4,

y = 14,4: 1,2,

y = 12,

Raspuns: 12

V. Munca independentă ținând cont de abilitățile individuale ale elevilor.

eu. Opțiune.

1. Pentru a rezolva ecuația 5x = -40, trebuie să împărțiți -40 la 5. Care este rădăcina acestei ecuații?

2. Subliniați coeficientul lui x și rezolvați ecuațiile:

a) 7x = 49;

6) - Zx = 111;

c) 12x = 1.

3. Rezolvând ecuația 12x = -744, a găsit Kolya, Ce x = -62. Înlocuind x cu 62, verificați dacă rădăcina ecuației este găsită corect.

4. Rezolvați ecuațiile.

a) 6x = 24;

b) 13x = -39;

c) 8x = 4;

d) 6x = 7,5; e)7x = 63;

e) - 4x = 12;

g) 9x = - 3;

h) 9x = 0,36.

5. La ce valoare a lui x:

a) valoarea expresiei 8x este -64;

b) valoarea expresiei 7x este 1;

c) valoarea expresiei -x este 11?

6. Mutați termenii care conțin x la stânga Parte ecuații, iar restul la dreapta, schimbându-se semnele lor la invers:

a) 2x - 3 = 5x + 8; c) -2x - 5 = 6x - 8;

b) 4x - 12 = -3x + 3; d) -4x - 2 = - 13x+ 21.

7. Completează soluția ecuației:

a) 2x - 4 = -8x + 12; b) 3x - 2 = 7x - 14;

c) 2x + 8x = 12 + 4 d) 3x - 7x = -14 + 2

8. Rezolvați ecuația:

a) 3x + 8 = x - 12;

b) x + 4 = 3 - 2x;

c) 5y = 2y + 16;

d) -2x + 9 - 8= x - 1.

9. Rezolvați ecuația:

a) 1,2x = -4,8; d) Zx - 4 = 11; g) 2x - 1 = 3x + 6;

b) -6x = 7,2; e) 5 - 2x = 0; h) x - 8 = 4x - 9;

B)-X = -0,6; e)-12 - x = 3; i) 5 - 6x = 0,3 - 5x.

10. La ce valoare a a

a) valoarea expresiei 3 + 2a este 43,

b) valoarea expresiei 12 - a este egală cu 100;

c) valorile expresiilor 13a + 17 și 5a + 9 sunt egale;

d) valorile expresiilor 5a + 14 și 2a + 7 sunt împotriva numere pozitive?

II. Opțiune

1. Pentru fiecare ecuație de forma ax = b, scrieți cu ce este egal a și cu ce este egal cu b:

a) 2,3x = 6,9;

b) –x = -1;

c) - x = 6;

d) 1,2x = 0.

2. a) Completați intrarea: pentru a rezolva ecuația ax = b, în ​​care a = 0, trebuie...

b) Rezolvați ecuația 12x = -60 și verificați.

3. Rezolvați ecuația:

1) a) 2x = 12; b) -5x = 15; c) - x = 32; d) -11x = 0;

2) a) 3x = 5; b) - 6x = -15; c) 29x = - 27; d) 16x = - 1;

3) a) 5x = 1/3|; b)4x = - 2/7; c) 1/3x = 6; d) -2/7x = 14.

4) a) 0,01x = 6,5; b) - 1,4x = 0,42; c) 0,3x = 10; d) -0,6x = - 0,5.

4. La ce valoare a lui x:

a) valoarea expresiei 5x este - 1;

b) valoarea expresiei -0,1x este 0,5;

c) valoarea expresiei 16x este 0?

5. Soluția unei ecuații de forma ax = b a fost scrisă pe tablă, dar partea dreaptă a ecuației a fost ștearsă. Restaurați-l:

a) 5x = ... b) 3x = ... c) 4x = ...

x = -12; x=1/6; x = 0,8.

6. Aflați valoarea lui a pentru care ecuația ax = 114 are rădăcina 6.

7. Rezolvați ecuația:

a) Zx-4 = 20

b) 54 - 5x ~ -6;

c) 1,2 - 0,Зх = 0;

d)16-7x = 0;

e) 5/6 = 1/6

8. Rezolvați ecuația:

a) 5x-11 = 2x+8; d) 0,8x-4 = 0,5-7;

b) 6-7x = 11-6x; e) 2,6x+8 = 2;

c) 3 - x = x+13; f) 12 + 1/3x = 15 - 1/6x

9. La ce valoare a:

a) valoarea expresiei 5-Za este 17;

b) semnificația expresiilor 3-2a și 5a+10 sunt egale;

c) valoarea expresiei 5 - 9a este cu 4 mai mare decât valoarea expresiei a+1;

d) valoarea expresiei 7+8a este cu 5 mai mică decât valoarea expresiei 2a+1?

10. Rezolvați ecuația:

a) 15(x+2) = 40; c) 5(2x+1) = 3(2x);

b) - 2(1-x) = x; d) -6(2-x)-5(1+x).

11. Rezolvați ecuația:

a) 43+4x+(11-5x) = 7; d) 6(x+11)-7x = 73+x;

b) 12-4x – (2+x) = 5x; e) 8(3x)- 12+6x = 25x;

c) 5x+12-3(x+16) = - 20; e) 6x-3(2-5x) - 12+8x.

Pentru autocontrol: după deschiderea parantezelor, se obține următoarea ecuație:

a) 43+4x+11-5x = 7; d) 6x+66-7x = 73+x;

b) 12-4x-2x = 5x; e) 24-8x-12+6x - 25x;

c) 5x+12-3x-48 = -20; e) 6x-6+15x = 12+8x.

III. Opțiune

1. Rezolvați ecuația:

a) 6x = 36; c) -x = 18; e) 49x = 0; g) 21x = - 3;

b) 5x=5/7; d)11x = -1/3; c) 1/3x = 0; e) -3/7x = - 1;

2. Rezolvați ecuația și verificați:

a) 0,08x - 1; c) – 0,1x = 1; e) 0,6x = - 5; g) – 0,3x = - 1,1;

b) 0.Зх = 1/3; d) – 1/7x = 0; f) 0,2x = 1/7 h) - 3,6x - - 6.

3. Alcătuiți o ecuație de forma ax = b, care

a) are ca rădăcină numărul 3;

b) are ca rădăcină numărul 0;

c) nu are rădăcini;

d) are infinit de rădăcini.

4. La ce valori ale lui x

A) valoarea expresiei 1/3x este 3;

b) valoarea expresiei - 0,8x este egală cu 0;

c) valoarea expresiei 0,01x este 30;

d) valoarea expresiei -15x este egală cu – 0,1.

5. După ce a rezolvat o ecuație de forma ax = b, elevul a șters coeficientul a. Restabiliți-l dacă este posibil:

a) …x = 1/8 b) …x = -4 c) …x = 0

x=4 x= - 1 x = 0

6 . Pentru ce valori întregi ale lui a este rădăcina ecuației ax = 8 un număr întreg?

8. Sunt date expresiile For+2 și a-5. La ce valori ale a

a) sensurile acestor expresii sunt egale;

b) valoarea primei expresii este cu 12 mai mare decât valoarea celei de-a doua;

c) valoarea primei expresii este cu 7 mai mică decât valoarea celei de-a doua;

d) valoarea primei expresii este de 5 ori mai mare decât valoarea celei de-a doua

rogo?

9. Rezolvați ecuația:

a) - (2x+1) = 41; d) 5(x-1) - 3(2x+2) = - 1;

b) 5(12) = 27; e) 12(1-x) - 4 = 2(4x+6);

c) 1,2(2x-1) = 3,6; e) 0,5(2x-1) - x = 6,5.

10. Pentru ecuația ax-11 = 3x+1, găsiți

a) valorile lui a pentru care rădăcina acestei ecuații este numărul 6;

b) valorile lui a la care această ecuație nu are rădăcini;

c) valorile naturale ale lui a, pentru care rădăcina ecuației este un număr natural.

11. Rezolvați ecuația:

a) 5(x - 18) - 7x = 21+x; d) 6(x - 1)+12(3 - 2x) = 45 - 17x;

b) 3x+6(1 - x) = - 2(2+x); e) 15(3 - x) - 5(x+11) = 1 - 19x;

c) 1,7 - 8(x - 1) = 3,7+2x; e) - (5 - x) - 8(6+x) = 11,8+x.

VI . Rezumatul lecției. Algoritm pentru reducerea unei ecuații la o ecuație liniară.

VII . Teme pentru acasă: clauza 3, nr. 128, 129, 131.

Verificarea a arătat că studenții au finalizat aceste sarcini, adică au stăpânit acest subiect.

Autoanaliza lecției

1. Într-o clasă sunt 25 de elevi. Cinci oameni pot studia pentru 4-5, 8 persoane pentru patru, restul nu pot studia fără îndrumare. La planificarea lecției, acest lucru a fost luat în considerare și a determinat alegerea metodelor și tehnicilor de prezentare a noului material și modalități de consolidare a cunoștințelor dobândite.

2. Aceasta este a doua lecție pe tema „Ecuații într-o singură variabilă”.În acest an școlar, acest material a fost studiat; la începutul lecției, cunoștințele au fost actualizate sub forma unui memento de către profesor a informațiilor necesare. Această lecție este importantă pentru studierea ulterioară a subiectului „Funcția liniară” într-un curs de algebră. Specific - multe concepte, modele, cunoștințe care sunt mai bine sistematizate și prezentate sub forma unui rezumat. Tip de lecție - lecție combinată.

3. Următoarele sarcini au fost rezolvate în timpul lecției:

Scopul didactic al lecției: Pentru a promova conștientizarea și înțelegerea noilor informații educaționale despre modelele geometrice și analitice ale unei ecuații liniare cu o variabilă.

Scop educativ: Formați conceptul de ecuație liniară și metodele de rezolvare a acesteia și obțineți o înțelegere a esenței numelui, a notației și a notației algebrice.

Scop de dezvoltare: Să promoveze dezvoltarea abilității de a modela o situație și de a sistematiza cunoștințele sub forma unui tabel.

Scop educativ: Formarea stimei de sine și a respectului pentru munca intelectuală.

Complexitatea soluției lor a fost gândită. Principalele au fost sarcini educaționale; în timpul rezolvării acestora, au fost rezolvate și sarcini de dezvoltare și educaționale. Sarcina de dezvoltare a fost rezolvată prin metode de studiu accesibil al materialului, iar sarcina educațională a fost rezolvată deja în etapa de alegere a unei clase pentru o lecție deschisă.

4. Această structură a lecției este dictată de incapacitatea elevilor de a absorbi materialul prezentat monoton timp îndelungat și cu concentrare. Prin urmare, lecția din prima jumătate este mai densă și mai dinamică. Sondajul a fost realizat pentru a actualiza cunoștințele existente și pentru a consolida altele noi. Legăturile dintre etape sunt logice. Tema pentru acasă conține trei numere, elevii pot completa câte doresc: pentru 3 - un număr, pentru 4 - două, pentru 5 - trei.

5. Accentul principal a fost pus pe conceptele: ecuație liniară, rădăcină a ecuației. Sunt selectate conceptele principale ale subiectului, sunt dezvoltate abilitățile de a denota, numi și scrie modelul algebric al unui interval numeric.

6. Metode de predare selectate parțial de căutare, vizual, bazat pe activitate.

7. Nu a fost nevoie să se folosească metode de predare diferențiate. Oferirea de asistență individuală este suficientă.

8. Controlul dobândirii cunoștințelor s-a realizat prin monitorizarea independenței și activității elevilor, pe măsură ce s-a studiat material nou.

9. Instrumente de instruire utilizate: Manual de Yu.N. Makarychev și alții - 2009, carduri pentru lucru oral și individual, tabla a fost utilizată în mod activ.

10. Sarcinile au fost pe deplin implementate.

În lecțiile anterioare, ne-am familiarizat cu expresiile și am învățat, de asemenea, cum să le simplificăm și să le calculăm. Acum trecem la ceva mai complex și mai interesant, și anume ecuații.

Ecuația și rădăcinile ei

Sunt numite egalități care conțin variabilă(e). ecuații. Rezolvați ecuația , înseamnă a găsi valoarea variabilei la care egalitatea va fi adevărată. Se numește valoarea variabilei rădăcina ecuației .

Ecuațiile pot avea o rădăcină, mai multe sau deloc.

La rezolvarea ecuațiilor se folosesc următoarele proprietăți:

• Dacă mutați un termen dintr-o ecuație dintr-o parte a ecuației în alta, schimbând semnul în cel opus, veți obține o ecuație echivalentă cu cea dată.
• Dacă ambele părți ale unei ecuații sunt înmulțite sau împărțite cu același număr, obțineți o ecuație echivalentă cu cea dată.

Exemplul nr. 1Care dintre numere: -2, -1, 0, 2, 3 sunt rădăcinile ecuației:

Pentru a rezolva această sarcină, trebuie pur și simplu să înlocuiți fiecare dintre numere pentru variabila x unul câte unul și să selectați acele numere pentru care egalitatea este considerată adevărată.

La „x= -2”:

\((-2)^2=10-3 \cdot (-2) \)

\(4=4\) - egalitatea este adevărată, ceea ce înseamnă că (-2) este rădăcina ecuației noastre

La „x= -1”

\((-1)^2=10-3 \cdot (-1) \)

\(1=7\) - egalitatea este falsă, prin urmare (-1) nu este rădăcina ecuației

\(0^2=10-3 \cdot 0 \)

\(0=10\) - egalitatea este falsă, deci 0 nu este rădăcina ecuației

\(2^2=10-3 \cdot 2\)

\(4=4\) - egalitatea este adevărată, ceea ce înseamnă că 2 este rădăcina ecuației noastre

\(3^2=10-3 \cdot 3 \)

\(9=1\) - egalitatea este falsă, deci 3 nu este rădăcina ecuației

Răspuns: din numerele prezentate, rădăcinile ecuației \(x^2=10-3x\) sunt numerele -2 și 2.

Ecuație liniară cu o variabilă sunt ecuații de forma ax = b, unde x este o variabilă, iar a și b sunt niște numere.

Există un număr mare de tipuri de ecuații, dar rezolvarea multora dintre ele se rezumă la rezolvarea ecuațiilor liniare, așa că cunoașterea acestui subiect este obligatorie pentru pregătirea ulterioară!

Exemplul nr. 2 Rezolvați ecuația: 4(x+7) = 3-x

Pentru a rezolva această ecuație, în primul rând, trebuie să scăpați de paranteză și, pentru a face acest lucru, înmulțiți fiecare dintre termenii din paranteză cu 4, obținem:

4x + 28 = 3 - x

Acum trebuie să mutăm toate valorile de la „x” într-o parte și totul în cealaltă parte (fără a uita să schimbăm semnul în cel opus), obținem:

4x + x = 3 - 28

Acum scade valoarea din stânga și dreapta:

Pentru a găsi factorul necunoscut (x), trebuie să împărțiți produsul (25) la factorul cunoscut (5):

Răspuns x = -5

Dacă vă îndoiți de răspuns, puteți verifica înlocuind valoarea rezultată în ecuația noastră în loc de x:

4(-5+7) = 3-(-5)

8 = 8 - ecuația este rezolvată corect!

Acum să rezolvăm ceva mai complicat:

Exemplul nr. 3 Aflați rădăcinile ecuației: \((y+4)-(y-4)=6y\)

În primul rând, să scăpăm și de paranteze:

Vedem imediat y și -y în partea stângă, ceea ce înseamnă că le puteți tăia pur și simplu și pur și simplu adăugați numerele rezultate și scrieți expresia:

Acum puteți muta valorile cu „y” la stânga, iar valorile cu numere la dreapta. Dar acest lucru nu este necesar, deoarece nu contează de ce parte sunt variabilele, principalul lucru este că acestea sunt fără numere, ceea ce înseamnă că nu vom transfera nimic. Dar pentru cei care nu înțeleg, vom face așa cum spune regula și vom împărți ambele părți la (-1), după cum spune proprietatea:

Pentru a găsi factorul necunoscut, trebuie să împărțiți produsul la factorul cunoscut:

\(y=\frac(8)(6) = \frac(4)(3) = 1\frac(1)(3) \)

Răspuns: y = \(1\frac(1)(3)\)

Puteți verifica și răspunsul, dar faceți-l singur.

Exemplul nr. 4\((0,5x+1,2)-(3,6-4,5x)=(4,8-0,3x)+(10,5x+0,6) \)

Acum o voi rezolva, fără explicații, și vă uitați la progresul soluției și la notația corectă pentru rezolvarea ecuațiilor:

\((0,5x+1,2)-(3,6-4,5x)=(4,8-0,3x)+(10,5x+0,6) \)

\(0,5x+1,2-3,6+4,5x=4,8-0,3x+10,5x+0,6\)

\(0,5x+4,5x+0,3x-10,5x=4,8+0,6-1,2+3,6\)

\(x=\frac(7,8)(-5,2)=\frac(3)(-2) =-1,5\)

Răspuns: x = -1,5

Dacă ceva nu este clar în timpul soluției, scrieți în comentarii.

Rezolvarea problemelor folosind ecuații

Știind ce sunt ecuațiile și învățând să le calculezi, îți oferi și acces la rezolvarea multor probleme în care ecuațiile sunt folosite pentru rezolvare.

Nu voi intra în teorie, este mai bine să arăt totul deodată cu exemple

Exemplul nr. 5 Erau de 2 ori mai puține mere în coș decât în ​​cutie. După ce 10 mere au fost transferate din coș în cutie, în cutie erau de 5 ori mai multe mere decât în ​​coș. Câte mere erau în coș și câte erau în cutie?

În primul rând, trebuie să stabilim ce vom accepta drept „x”, în această problemă putem accepta atât cutii, cât și coșuri, dar voi lua merele în coș.

Deci, să fie x mere în coș, deoarece erau de două ori mai multe mere în cutie, atunci să luăm asta ca de două ori. După ce merele au fost transferate din coș în cutie, numărul de mere din coș a devenit: x - 10, ceea ce înseamnă că erau - (2x + 10) mere în cutie.

Acum putem crea ecuația:

5(x-10) - sunt de 5 ori mai multe mere în cutie decât în ​​coș.

Să echivalăm prima valoare și a doua:

2x+10 = 5(x-10) și rezolvă:

2x + 10 = 5x - 50

2x - 5x = -50 - 10

x = -60/-3 = 20 (mere) - în coș

Acum, știind câte mere au fost în coș, să aflăm câte mere au fost în cutie - deoarece au fost de două ori mai multe, pur și simplu vom înmulți rezultatul cu 2:

2*20 = 40 (mere) - într-o cutie

Răspuns: într-o cutie sunt 40 de mere și într-un coș 20 de mere.

Înțeleg că mulți dintre voi poate nu ați înțeles pe deplin cum să rezolvați problemele, dar vă asigur că vom reveni asupra acestui subiect de mai multe ori în lecțiile noastre, dar între timp, dacă mai aveți întrebări, adresați-le în comentarii. .

În sfârșit, încă câteva exemple despre rezolvarea ecuațiilor

Exemplul nr. 6\(2x - 0,7x = 0\)

Exemplul nr. 7\(3p - 1 -(p+3) = 1 \)

Exemplul nr. 8\(6y-(y-1) = 4+5y\)

\(6y-y+1=4+5y\)

\(6y-y-5y=4-1\)

\(0y=3 \) - nu există rădăcini, deoarece Nu poți împărți la zero!

Vă mulțumesc tuturor pentru atenție. Dacă ceva nu este clar, întrebați în comentarii.

Javascript este dezactivat în browserul dvs.
Pentru a efectua calcule, trebuie să activați controalele ActiveX!

Ecuație liniară cu o variabilă

Testul nr. 1

Ţintă:

Arătați abilități în însușirea temei „Ecuație liniară cu o variabilă” Să fie capabil să compună o expresie cu variabile în funcție de condițiile problemei. Transformați expresii: adăugați termeni similari, deschideți paranteze. Găsiți valoarea unei expresii cu variabile având în vedere valorile variabilelor.

Sarcina nr. 1

• Rezolvați ecuația:

• 1 opțiune

• a) 6x- 15 = 4x + 11;
• b) 9 – 7(x+3) = 5 – 4x.

• Opțiunea 2

• a) 9x – 8=4x + 12;
• b) 6 – 8 (x+2) = 3 – 2x.

Sarcina nr. 2

• 1 opțiune

Prima cutie conținea de 5 ori mai multe mere decât a doua. Când s-au luat 7 kg de mere din prima cutie și s-au adăugat 5 kg la a doua, atunci numărul de mere din cutii a devenit egal. Câte kg. Au fost mere în fiecare cutie la început?

• Opțiunea 2

Primul coș conținea de 4 ori mai multe ciuperci decât al doilea. Când în primul coș au fost puse încă 4 ciuperci și în al doilea 31 de ciuperci, atunci în coșuri era un număr egal de ciuperci. Câte ciuperci erau la început în fiecare coș?

Sarcina nr. 3

• Rezolvați ecuația:

• 1 opțiune

a) (8y – 16) · (2,1 + 0,3y) = 0;

b) 7x – (4x + 3) = 3x + 2.

• Opțiunea 2

a) (12y + 30) · (1,4 – 0,7y) = 0;

b) 9x – (5x – 4) = 4x + 4.

Sarcina nr. 4

• 1 opțiune

100 kg au fost livrate la primul magazin dulciuri, iar în al doilea - 240 kg. Primul magazin vindea zilnic 12 kg de dulciuri, iar al doilea - 46 kg. După câte zile va avea al doilea magazin de 4 ori mai puține bomboane decât primul?

• Opțiunea 2

În primul depozit erau 300 de tone de cărbune, iar în al doilea - 178 de tone, din primul depozit se exportau zilnic 15 tone de cărbune, iar din al doilea 18 tone. După câte zile vor rămâne de 3 ori mai multe tone de cărbune în primul depozit decât în ​​al doilea?

Sarcina nr. 5

• 1 opțiune

La ce valoare a lui a are ecuația (a + 3)x = 12

a) are rădăcina egală cu 6;

b) nu are rădăcini?

• Opțiunea 2

La ce valoare a lui a are ecuația (a -2)x = 35

a) are rădăcina egală cu 5;

Ecuația este o egalitate în care sunt prezente una sau mai multe variabile.
Vom lua în considerare cazul în care ecuația are o variabilă, adică un număr necunoscut. În esență, o ecuație este un tip de model matematic. Prin urmare, în primul rând, avem nevoie de ecuații pentru a rezolva probleme.

Să ne amintim cum este compilat un model matematic pentru a rezolva o problemă.
De exemplu, în noul an universitar numărul elevilor de la școala nr. 5 s-a dublat. După ce 20 de elevi s-au mutat într-o altă școală, în total 720 de elevi au început să învețe la școala nr. 5. Câți studenți au fost anul trecut?

Trebuie să exprimăm ceea ce se spune în condiție în limbaj matematic. Fie numărul de studenți anul trecut X. Apoi, în funcție de condițiile problemei,
2X – 20 = 720. Avem un model matematic care reprezintă ecuație cu o variabilă. Mai exact, este o ecuație de gradul I cu o variabilă. Tot ce rămâne este să-i găsești rădăcina.

Care este rădăcina unei ecuații?

Valoarea variabilei la care ecuația noastră se transformă într-o egalitate adevărată se numește rădăcina ecuației. Există ecuații care au multe rădăcini. De exemplu, în ecuația 2*X = (5-3)*X, orice valoare a lui X este o rădăcină. Și ecuația X = X +5 nu are deloc rădăcini, deoarece indiferent de ce valoare înlocuim X, nu vom obține egalitatea corectă. Rezolvarea unei ecuații înseamnă găsirea tuturor rădăcinilor sau determinarea faptului că nu are rădăcini. Deci, pentru a răspunde la întrebarea noastră, trebuie să rezolvăm ecuația 2X – 20 = 720.

Cum se rezolvă ecuații cu o variabilă?

Mai întâi, să scriem câteva definiții de bază. Fiecare ecuație are o parte dreaptă și o parte stângă. În cazul nostru, (2X – 20) este partea stângă a ecuației (este la stânga semnului egal), iar 720 este partea dreaptă a ecuației. Termenii din partea dreaptă și stângă a ecuației se numesc termeni ai ecuației. Termenii ecuației noastre sunt 2X, -20 și 720.

Să vorbim imediat despre 2 proprietăți ale ecuațiilor:

1. Orice termen al ecuației poate fi transferat din partea dreaptă a ecuației în stânga și invers. În acest caz, este necesar să schimbați semnul acestui termen al ecuației la opus. Adică, înregistrările de forma 2X – 20 = 720, 2X – 20 – 720 = 0, 2X = 720 + 20, -20 = 720 – 2X sunt echivalente.
2. Ambele părți ale ecuației pot fi înmulțite sau împărțite cu același număr. Acest număr nu trebuie să fie zero. Adică, înregistrările de forma 2X – 20 = 720, 5*(2X – 20) = 720*5, (2X – 20):2 = 720:2 sunt de asemenea echivalente.

Să folosim aceste proprietăți pentru a ne rezolva ecuația.

Să ne mișcăm -20 în partea dreaptă cu semnul opus. Primim:

2X = 720 + 20. Să adăugăm ce avem în partea dreaptă. Obținem că 2X = 740.

Acum împărțiți părțile stânga și dreaptă ale ecuației la 2.

2X:2 = 740:2 sau X = 370. Am găsit rădăcina ecuației noastre și, în același timp, am găsit răspunsul la întrebarea problemei noastre. Anul trecut au fost 370 de elevi la școala nr.5.

Să verificăm dacă rădăcina noastră transformă într-adevăr ecuația într-o egalitate adevărată. Să înlocuim numărul 370 în loc de X în ecuația 2X – 20 = 720.

2*370-20 = 720.

Asta e corect.

Deci, pentru a rezolva o ecuație cu o variabilă, aceasta trebuie redusă la o așa-numită ecuație liniară de forma ax = b, unde a și b sunt niște numere. Apoi împărțiți părțile din stânga și din dreapta la numărul a. Obținem că x = b:a.

Ce înseamnă reducerea unei ecuații la o ecuație liniară?

Luați în considerare această ecuație:

5X - 2X + 10 = 59 - 7X +3X.

Aceasta este, de asemenea, o ecuație cu o variabilă necunoscută X. Sarcina noastră este să reducem această ecuație la forma ax = b.

Pentru a face acest lucru, colectăm mai întâi toți termenii care au X ca factor în partea stângă a ecuației, iar termenii rămași în partea dreaptă. Termenii care au aceeași literă ca factor se numesc termeni similari.

5X - 2X + 7X – 3X = 59 – 10.

Conform proprietății distributive a înmulțirii, putem scoate același factor din paranteze și adăugați coeficienții (multiplicatori pentru variabila x). Acest proces se mai numește și reducerea termenilor similari.

X(5-2+7-3) = 49.

7X = 49. Am redus ecuația la forma ax = b, unde a = 7, b = 49.

Și așa cum am scris mai sus, rădăcina unei ecuații de forma ax = b este x = b:a.

Adică X = 49:7 = 7.

Algoritm pentru găsirea rădăcinilor unei ecuații cu o variabilă.

1. Colectați termeni similari în partea stângă a ecuației, iar termenii rămași în partea dreaptă a ecuației.
2. Dați termeni similari.
3. Reduceți ecuația la forma ax = b.
4. Găsiți rădăcinile folosind formula x = b:a.

Notă. În acest articol, nu am luat în considerare acele cazuri în care o variabilă este ridicată la orice putere. Cu alte cuvinte, am luat în considerare ecuații de gradul întâi cu o variabilă.

În acest articol vom considera principiul rezolvării unor astfel de ecuații ca ecuații liniare. Să notăm definiția acestor ecuații și să stabilim forma generală. Vom analiza toate condițiile pentru găsirea soluțiilor ecuațiilor liniare, folosind, printre altele, exemple practice.

Vă rugăm să rețineți că materialul de mai jos conține informații despre ecuații liniare cu o variabilă. Ecuațiile liniare din două variabile sunt discutate într-un articol separat.

Ce este o ecuație liniară

Definiția 1

Ecuație liniară este o ecuație scrisă după cum urmează:
a x = b, Unde X- variabil, AȘi b- unele numere.

Această formulare a fost folosită în manualul de algebră (clasa a VII-a) de Yu.N. Makarychev.

Exemplul 1

Exemple de ecuații liniare ar fi:

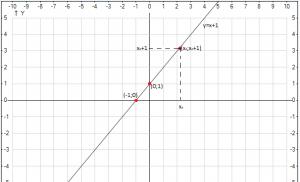
3 x = 11(ecuația cu o variabilă X la a = 5Și b = 10);

− 3 , 1 y = 0 ( ecuație liniară cu variabilă y, Unde a = - 3, 1Și b = 0);

x = − 4Și − x = 5,37(ecuații liniare, unde numărul A scris explicit și egal cu 1 și respectiv - 1. Pentru prima ecuație b = - 4; pentru al doilea - b = 5,37) și așa mai departe.

Materiale educaționale diferite pot avea definiții diferite. De exemplu, Vilenkin N.Ya. Ecuațiile liniare includ și acele ecuații care pot fi transformate în formă a x = b prin transferul de termeni dintr-o parte in alta cu schimbare de semn si aducerea unor termeni similari. Dacă urmărim această interpretare, ecuația 5 x = 2 x + 6 – de asemenea liniară.

Dar manualul de algebră (clasa a VII-a) de Mordkovich A.G. ofera urmatoarea descriere:

Definiția 2

O ecuație liniară într-o variabilă x este o ecuație de formă a x + b = 0, Unde AȘi b– unele numere numite coeficienți ai unei ecuații liniare.

Exemplul 2

Un exemplu de ecuații liniare de acest tip ar putea fi:

3 x − 7 = 0 (a = 3 , b = − 7) ;

1, 8 y + 7, 9 = 0 (a = 1, 8, b = 7, 9).

Dar există și exemple de ecuații liniare pe care le-am folosit deja mai sus: de formă a x = b, De exemplu, 6 x = 35.

Vom fi imediat de acord că în acest articol printr-o ecuație liniară cu o variabilă vom înțelege ecuația scrisă a x + b = 0, Unde X- variabil; a, b – coeficienți. Vedem această formă a unei ecuații liniare ca fiind cea mai justificată, deoarece ecuațiile liniare sunt ecuații algebrice de gradul întâi. Și celelalte ecuații indicate mai sus, și ecuațiile date prin transformări echivalente în formă a x + b = 0, definim drept ecuații care se reduc la ecuații liniare.

Cu această abordare, ecuația 5 x + 8 = 0 este liniară și 5 x = − 8- o ecuație care se reduce la una liniară.

Principiul rezolvării ecuațiilor liniare

Să ne uităm la cum să determinăm dacă o anumită ecuație liniară va avea rădăcini și, dacă da, câte și cum să le determinăm.

Definiția 3

Faptul prezenței rădăcinilor unei ecuații liniare este determinat de valorile coeficienților AȘi b. Să notăm aceste condiții:

• la a ≠ 0 ecuația liniară are o singură rădăcină x = - b a ;
• la a = 0Și b ≠ 0 o ecuație liniară nu are rădăcini;
• la a = 0Și b = 0 o ecuație liniară are infinit de rădăcini. În esență, în acest caz, orice număr poate deveni rădăcina unei ecuații liniare.

Să dăm o explicație. Știm că în procesul de rezolvare a unei ecuații este posibil să se transforme o ecuație dată într-una echivalentă, ceea ce înseamnă că are aceleași rădăcini ca și ecuația originală sau, de asemenea, nu are rădăcini. Putem face următoarele transformări echivalente:

• transferați un termen dintr-o parte în alta, schimbând semnul în opus;
• înmulțiți sau împărțiți ambele părți ale unei ecuații cu același număr care nu este zero.

Astfel, transformăm ecuația liniară a x + b = 0, mutând termenul b din partea stângă în partea dreaptă cu schimbare de semn. Primim: a · x = − b .

Deci, împărțim ambele părți ale ecuației la un număr diferit de zero A, rezultând o egalitate de forma x = - b a . Adică când a ≠ 0, ecuația originală a x + b = 0 este echivalentă cu egalitatea x = - b a, în care rădăcina - b a este evidentă.

Prin contradicție se poate demonstra că rădăcina găsită este singura. Să desemnăm rădăcina găsită - b a ca x 1 . Să presupunem că există o altă rădăcină a ecuației liniare cu denumirea x 2 .Și, desigur: x 2 ≠ x 1, iar aceasta, la rândul său, bazată pe definirea numerelor egale prin diferență, este echivalentă cu condiția x 1 − x 2 ≠ 0 .Ținând cont de cele de mai sus, putem crea următoarele egalități prin înlocuirea rădăcinilor:
a x 1 + b = 0și a x 2 + b = 0.
Proprietatea egalităților numerice face posibilă scăderea termen cu termen a părților egalităților:

a x 1 + b − (a x 2 + b) = 0 − 0, de aici: a · (x 1 − x 2) + (b − b) = 0 si mai departe a · (x 1 − x 2) = 0 . Egalitatea a · (x 1 − x 2) = 0 este incorectă deoarece s-a specificat anterior că a ≠ 0Și x 1 − x 2 ≠ 0 . Contradicția rezultată servește drept dovadă că atunci când a ≠ 0 ecuație liniară a x + b = 0 are o singură rădăcină.

Să justificăm încă două clauze din condițiile care conțin a = 0.

Când a = 0 ecuație liniară a x + b = 0 va fi scris ca 0 x + b = 0. Proprietatea de a înmulți un număr cu zero ne dă dreptul de a afirma că orice număr este luat ca X, substituind-o în egalitate 0 x + b = 0, obținem b = 0 . Egalitatea este valabilă pentru b = 0; în alte cazuri, când b ≠ 0, egalitatea devine falsă.

Deci când a = 0și b = 0 , orice număr poate deveni rădăcina unei ecuații liniare a x + b = 0, deoarece atunci când aceste condiții sunt îndeplinite, înlocuind în schimb X orice număr, obținem egalitatea numerică corectă 0 = 0 . Când a = 0Și b ≠ 0 ecuație liniară a x + b = 0 nu va avea deloc rădăcini, deoarece atunci când sunt îndeplinite condițiile specificate, înlocuind în schimb X orice număr, obținem o egalitate numerică incorectă b = 0.

Toate considerațiile de mai sus ne oferă posibilitatea de a scrie un algoritm care face posibilă găsirea unei soluții pentru orice ecuație liniară:

• după tipul de înregistrare determinăm valorile coeficienților AȘi bși analizați-le;
• la a = 0Și b = 0 ecuația va avea infinit de rădăcini, adică. orice număr va deveni rădăcina ecuației date;
• la a = 0Și b ≠ 0
• la A, diferit de zero, începem să căutăm singura rădăcină a ecuației liniare originale:

1. hai sa mutam coeficientul bîn partea dreaptă cu schimbare de semn la opus, aducând ecuația liniară la formă a · x = − b ;
2. împărțiți ambele părți ale egalității rezultate la număr A, care ne va da rădăcina dorită a ecuației date: x = - b a.

De fapt, secvența de acțiuni descrisă este răspunsul la întrebarea cum să găsești o soluție la o ecuație liniară.

În cele din urmă, să clarificăm acele ecuații ale formei a x = b sunt rezolvate folosind un algoritm similar cu singura diferență că numărul bîntr-o astfel de notație a fost deja transferat la partea necesară a ecuației și cu a ≠ 0 puteți împărți imediat părțile unei ecuații la un număr A.

Astfel, pentru a găsi o soluție la ecuație a x = b, folosim urmatorul algoritm:

• la a = 0Și b = 0 ecuația va avea infinit de rădăcini, adică. orice număr poate deveni rădăcină;
• la a = 0Și b ≠ 0 ecuația dată nu va avea rădăcini;
• la A, nu este egal cu zero, ambele părți ale ecuației sunt împărțite la număr A, ceea ce face posibilă găsirea singurei rădăcini care este egală cu b a.

Exemple de rezolvare a ecuațiilor liniare

Exemplul 3

Ecuația liniară trebuie rezolvată 0 x − 0 = 0.

Soluţie

Scriind ecuația dată vedem că a = 0Și b = − 0(sau b = 0, care este la fel). Astfel, o ecuație dată poate avea un număr infinit de rădăcini sau orice număr.

Răspuns: X- orice număr.

Exemplul 4

Este necesar să se determine dacă ecuația are rădăcini 0 x + 2, 7 = 0.

Soluţie

Din înregistrare determinăm că a = 0, b = 2, 7. Astfel, ecuația dată nu va avea rădăcini.

Răspuns: ecuația liniară inițială nu are rădăcini.

Exemplul 5

Dată o ecuație liniară 0,3 x − 0,027 = 0. Trebuie rezolvat.

Soluţie

Scriind ecuația determinăm că a = 0, 3; b = - 0,027, ceea ce ne permite să afirmăm că ecuația dată are o singură rădăcină.

Urmând algoritmul, mutăm b în partea dreaptă a ecuației, schimbând semnul, obținem: 0,3 x = 0,027. Apoi, împărțim ambele părți ale egalității rezultate la a = 0, 3, apoi: x = 0, 027 0, 3.

Să împărțim fracțiile zecimale:

0,027 0,3 = 27 300 = 3 9 3 100 = 9 100 = 0,09

Rezultatul obținut este rădăcina ecuației date.

Să scriem pe scurt soluția după cum urmează:

0,3 x - 0,027 = 0,0,3 x = 0,027, x = 0,027 0,3, x = 0,09.

Răspuns: x = 0,09.

Pentru claritate, prezentăm soluția ecuației de scriere a x = b.

Exemplul N

Ecuaţiile date sunt: ​​1) 0 x = 0 ; 2) 0 x = − 9 ; 3) - 3 8 x = - 3 3 4 . Ele trebuie rezolvate.

Soluţie

Toate ecuațiile date corespund intrării a x = b. Să le privim unul câte unul.

În ecuația 0 x = 0, a = 0 și b = 0, ceea ce înseamnă: orice număr poate fi rădăcina acestei ecuații.

În a doua ecuație 0 x = − 9: a = 0 și b = − 9, astfel, această ecuație nu va avea rădăcini.

Pe baza formei ultimei ecuații - 3 8 · x = - 3 3 4, scriem coeficienții: a = - 3 8, b = - 3 3 4, adică. ecuația are o singură rădăcină. Să-l găsim. Să împărțim ambele părți ale ecuației cu a, rezultând: x = - 3 3 4 - 3 8. Să simplificăm fracția aplicând regula de împărțire a numerelor negative, urmată de conversia numărului mixt într-o fracție obișnuită și împărțirea fracțiilor ordinare:

3 3 4 - 3 8 = 3 3 4 3 8 = 15 4 3 8 = 15 4 8 3 = 15 8 4 3 = 10

Să scriem pe scurt soluția după cum urmează:

3 8 · x = - 3 3 4 , x = - 3 3 4 - 3 8 , x = 10 .

Răspuns: 1) X– orice număr, 2) ecuația nu are rădăcini, 3) x = 10.

Dacă observați o eroare în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter