Spirala Fibonacci este o lege criptată a naturii. Numerele Fibonacci: în căutarea secretului universului șirul de numere Fibonacci din natură

Există încă multe mistere nerezolvate în univers, dintre care unele oamenii de știință au reușit deja să le identifice și să le descrie. Numerele Fibonacci și raportul de aur formează baza pentru dezlegarea lumii din jurul nostru, construindu-i forma și percepția vizuală optimă de către o persoană, cu ajutorul căreia poate simți frumusețea și armonia.

ratia de aur

Principiul determinării dimensiunii secțiunii de aur stă la baza perfecțiunii întregii lumi și a părților sale în structura și funcțiile sale, manifestarea ei poate fi văzută în natură, artă și tehnologie. Doctrina raportului de aur a fost fondată ca rezultat al cercetărilor efectuate de oamenii de știință antici asupra naturii numerelor.

Se bazează pe teoria proporțiilor și raporturilor diviziunilor segmentelor, care a fost realizată de filosoful și matematicianul antic Pitagora. El a demonstrat că atunci când se împarte un segment în două părți: X (mai mic) și Y (mai mare), raportul dintre cel mai mare și cel mai mic va fi egal cu raportul dintre suma lor (a întregului segment):

Rezultatul este o ecuație: x 2 - x - 1=0, care se rezolvă ca x=(1±√5)/2.

Dacă luăm în considerare raportul 1/x, atunci este egal cu 1,618…

Dovada utilizării raportului de aur de către gânditorii antici este dată în cartea „Începuturilor” lui Euclid, scrisă încă din secolul al III-lea. BC, care a folosit această regulă pentru a construi 5-gonuri obișnuite. Printre pitagoreeni, această figură este considerată sacră, deoarece este atât simetrică, cât și asimetrică. Pentagrama simbolizează viața și sănătatea.

numerele Fibonacci

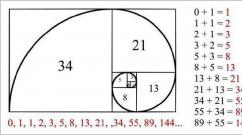
Celebra carte Liber abaci a matematicianului italian Leonardo din Pisa, care mai târziu a devenit cunoscut sub numele de Fibonacci, a fost publicată în 1202. În ea, omul de știință oferă pentru prima dată un model de numere, într-o serie a cărora fiecare număr este suma. din cele 2 cifre anterioare. Secvența numerelor Fibonacci este următoarea:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 etc.

Omul de știință a citat, de asemenea, o serie de modele:

• Orice număr din serie, împărțit la următorul, va fi egal cu o valoare care tinde spre 0,618. Mai mult, primele numere Fibonacci nu dau un astfel de număr, dar pe măsură ce te deplasezi de la începutul secvenței, acest raport va fi din ce în ce mai precis.
• Dacă împărțiți numărul din serie la cel precedent, atunci rezultatul va tinde spre 1,618.
• Un număr împărțit la următorul va arăta o valoare care tinde spre 0,382.

Aplicarea conexiunii și modelelor secțiunii de aur, numărul Fibonacci (0,618) poate fi găsită nu numai în matematică, ci și în natură, în istorie, în arhitectură și construcții și în multe alte științe.

Spirala lui Arhimede și dreptunghi auriu

Spiralele, foarte comune în natură, au fost explorate de Arhimede, care a derivat chiar și ecuația ei. Forma spiralei se bazează pe legile raportului de aur. Când este nerăsucită, se obține o lungime căreia i se pot aplica proporții și numere Fibonacci, creșterea pasului are loc uniform.

Paralela dintre numerele Fibonacci și raportul de aur poate fi văzută și prin construirea unui „dreptunghi de aur” ale cărui laturi sunt proporționale ca 1,618:1. Se construiește prin trecerea de la un dreptunghi mai mare la unul mai mic, astfel încât lungimile laturilor să fie egale cu numerele din rând. Construcția sa se poate face în ordine inversă, începând cu pătratul „1”. La conectarea colțurilor acestui dreptunghi cu linii în centrul intersecției lor, se obține o spirală Fibonacci sau logaritmică.

Istoria utilizării proporțiilor de aur

Multe monumente arhitecturale antice ale Egiptului au fost ridicate folosind proporții de aur: celebrele piramide ale lui Keops și altele.Arhitecții Greciei Antice le-au folosit pe scară largă în construcția de obiecte de arhitectură, cum ar fi temple, amfiteatre, stadioane. De exemplu, astfel de proporții au fost folosite în construcția templului antic Partenon (Atena) și a altor obiecte care au devenit capodopere ale arhitecturii antice, demonstrând armonie bazată pe regularitatea matematică.

În secolele ulterioare, interesul pentru raportul de aur a scăzut, iar tiparele au fost uitate, dar din nou reluate în Renaștere, împreună cu cartea călugărului franciscan L. Pacioli di Borgo „Proporția divină” (1509). Include ilustrații de Leonardo da Vinci, care a fixat noul nume „secțiunea de aur”. De asemenea, 12 proprietăți ale proporției de aur au fost dovedite științific, iar autorul a vorbit despre modul în care se manifestă în natură, în artă și a numit-o „principiul construirii lumii și naturii”.

Omul Vitruvian Leonardo

Desenul prin care Leonardo da Vinci a ilustrat cartea lui Vitruvius în 1492 înfățișează o figură a unui bărbat în 2 poziții cu brațele întinse în lateral. Figura este înscrisă într-un cerc și un pătrat. Acest desen este considerat a fi proporțiile canonice ale corpului uman (mascul), descrise de Leonardo pe baza studiului lor în tratatele arhitectului roman Vitruvius.

Centrul corpului ca punct echidistant față de capătul brațelor și picioarelor este buricul, lungimea brațelor este egală cu înălțimea unei persoane, lățimea maximă a umerilor = 1/8 din înălțime, distanța de la vârful pieptului până la păr = 1/7, de la vârful pieptului până la vârful capului = 1/6 etc.

De atunci, desenul a fost folosit ca simbol care arată simetria internă a corpului uman.

Termenul „Proporția de Aur” a fost folosit de Leonardo pentru a desemna relații proporționale în figura umană. De exemplu, distanța de la talie la picioare este legată de aceeași distanță de la buric până la vârful capului la fel ca înălțimea până la prima lungime (de la talie în jos). Acest calcul se face similar cu raportul segmentelor atunci când se calculează raportul de aur și tinde spre 1,618.

Toate aceste proporții armonioase sunt adesea folosite de artiști pentru a crea lucrări frumoase și impresionante.

Studii ale raportului de aur în secolele XVI-XIX

Folosind raportul de aur și numerele Fibonacci, lucrările de cercetare privind problema proporțiilor se desfășoară de mai bine de un secol. În paralel cu Leonardo da Vinci, artistul german Albrecht Dürer dezvolta și teoria proporțiilor corecte ale corpului uman. Pentru aceasta, a creat chiar și o busolă specială.

În secolul al XVI-lea problema conexiunii dintre numărul Fibonacci și secțiunea de aur a fost dedicată lucrării astronomului I. Kepler, care a aplicat pentru prima dată aceste reguli botanicii.

O nouă „descoperire” aștepta raportul de aur în secolul al XIX-lea. odată cu publicarea „Cercetării estetice” de către omul de știință german profesor Zeisig. El a ridicat aceste proporții la absolut și a anunțat că sunt universale pentru toate fenomenele naturale. El a efectuat studii asupra unui număr mare de oameni, sau mai degrabă asupra proporțiilor lor corporale (aproximativ 2 mii), în urma cărora s-au tras concluzii despre modele confirmate statistic în raporturile diferitelor părți ale corpului: lungimea umerilor, antebrațelor. , mâinile, degetele etc.

Au fost studiate și obiectele de artă (vaze, structuri arhitecturale), tonurile muzicale, dimensiunile la scrierea poeziei - Zeisig a afișat toate acestea prin lungimile segmentelor și numerelor, a introdus și termenul de „estetică matematică”. După primirea rezultatelor, s-a dovedit că se obține seria Fibonacci.

Numărul Fibonacci și raportul de aur în natură

În lumea vegetală și animală, există o tendință de formare sub formă de simetrie, care se observă în direcția creșterii și mișcării. Împărțirea în părți simetrice în care se observă proporțiile de aur este un model inerent multor plante și animale.

Natura din jurul nostru poate fi descrisă folosind numerele Fibonacci, de exemplu:

• dispunerea frunzelor sau ramurilor oricăror plante, precum și distanțele, sunt legate de seria numerelor date 1, 1, 2, 3, 5, 8, 13 și așa mai departe;
• seminte de floarea soarelui (solzi pe conuri, celule de ananas), dispuse in doua randuri in spirale rasucite in directii diferite;
• raportul dintre lungimea cozii și întregul corp al șopârlei;
• forma oului, dacă trasați o linie condiționat prin partea sa largă;
• raportul dintre dimensiunea degetelor de pe mâna omului.

Și, desigur, cele mai interesante forme sunt cochiliile de melci în spirală, modelele de pe web, mișcarea vântului în interiorul unui uragan, dubla helix în ADN și structura galaxiilor - toate acestea includ o secvență de Fibonacci. numere.

Utilizarea raportului de aur în art

Cercetătorii care caută exemple de utilizare a secțiunii de aur în artă examinează în detaliu diverse obiecte de arhitectură și picturi. Sunt cunoscute lucrări sculpturale celebre, creatorii cărora au aderat la proporții de aur - statuile lui Zeus Olimpian, Apollo Belvedere și

Una dintre creațiile lui Leonardo da Vinci – „Portretul Mona Lisei” – a făcut obiectul cercetărilor oamenilor de știință de mulți ani. Ei au descoperit că compoziția lucrării constă în întregime din „triunghiuri de aur”, unite împreună într-o stea pentagon obișnuită. Toate lucrările lui da Vinci sunt dovada cât de profunde erau cunoștințele sale despre structura și proporțiile corpului uman, datorită cărora a reușit să surprindă zâmbetul incredibil de misterios al Mona Lisei.

Raportul de aur în arhitectură

De exemplu, oamenii de știință au studiat capodopere arhitecturale create după regulile „secțiunii de aur”: piramidele egiptene, Panteonul, Partenonul, Catedrala Notre Dame de Paris, Catedrala Sf. Vasile etc.

Partenonul, una dintre cele mai frumoase clădiri din Grecia Antică (sec. V î.Hr.), are 8 coloane și 17 pe laturi diferite, raportul dintre înălțimea sa și lungimea laturilor este de 0,618. Proeminențele de pe fațadele sale sunt realizate conform „secțiunii de aur” (foto de mai jos).

Unul dintre oamenii de știință care a inventat și aplicat cu succes îmbunătățirea sistemului modular de proporții pentru obiectele de arhitectură (așa-numitul „modulor”) a fost arhitectul francez Le Corbusier. Modulorul se bazează pe un sistem de măsurare asociat cu o împărțire condiționată în părți ale corpului uman.

Arhitectul rus M. Kazakov, care a construit mai multe clădiri rezidențiale la Moscova, precum și clădirile Senatului din Kremlin și Spitalul Golitsyn (acum Prima Clinică numită după N.I. Pirogov), a fost unul dintre arhitecții care au folosit legile în proiectarea și construcția despre raportul de aur.

Aplicarea proporțiilor în proiectare

În designul de modă, toți designerii de modă realizează imagini și modele noi, ținând cont de proporțiile corpului uman și de regulile raportului de aur, deși prin natura lor nu toți oamenii au proporții ideale.

Atunci când se planifica amenajarea peisajului și se creează compoziții volumetrice de parc cu ajutorul plantelor (copaci și arbuști), fântâni și mici obiecte de arhitectură, se pot aplica și modelele de „proporții divine”. La urma urmei, compoziția parcului ar trebui să se concentreze pe crearea unei impresii asupra vizitatorului, care va putea să navigheze liber în el și să găsească centrul compozițional.

Toate elementele parcului sunt în asemenea proporții încât, cu ajutorul structurii geometrice, al aranjamentului reciproc, al luminii și al luminii, dau impresia de armonie și perfecțiune asupra unei persoane.

Aplicarea secțiunii de aur în cibernetică și tehnologie

Legile secțiunii de aur și numerele Fibonacci se manifestă și în tranzițiile energetice, în procese care au loc cu particule elementare care alcătuiesc compușii chimici, în sistemele spațiale, în structura genei ADN.

Procese similare apar în corpul uman, manifestându-se în bioritmurile vieții sale, în acțiunea organelor, de exemplu, creierul sau vederea.

Algoritmii și modelele de proporții de aur sunt utilizate pe scară largă în cibernetica și informatica modernă. Una dintre sarcinile simple pe care programatorii începători trebuie să le rezolve este să scrie o formulă și să determine suma numerelor Fibonacci până la un anumit număr folosind limbaje de programare.

Cercetări moderne asupra teoriei raportului de aur

De la mijlocul secolului al XX-lea, interesul pentru problemele și influența legilor proporțiilor de aur asupra vieții umane a crescut dramatic și din partea multor oameni de știință de diverse profesii: matematicieni, cercetători etnici, biologi, filozofi, lucrători medicali, economiști, muzicieni etc.

Din anii 1970, The Fibonacci Quarterly a fost publicat în Statele Unite, unde sunt publicate lucrări pe această temă. În presă apar lucrări în care regulile generalizate ale secțiunii de aur și seria Fibonacci sunt folosite în diferite ramuri ale cunoașterii. De exemplu, pentru codificarea informațiilor, cercetări chimice, biologice etc.

Toate acestea confirmă concluziile oamenilor de știință antici și moderni conform cărora raportul de aur este conectat multilateral cu problemele fundamentale ale științei și se manifestă în simetria multor creații și fenomene ale lumii din jurul nostru.

El va spune despre conceptul seriei Fibonacci și despre modul în care acesta este conectat cu teoria undelor și, de asemenea, va respinge aplicabilitatea seriei la procesele naturale.
, pe care maestrul l-a dezvoltat în anii 30 ai secolului trecut - aceasta este una dintre cele mai interesante secțiuni. În sine, a fost evidențiat într-un nou capitol al științei care studiază graficele. Se bazează pe evoluțiile altor specialiști în domeniul teoriei (te sfătuiesc să citești - o carte sub paternitate).
Deci, de exemplu, marele matematician italian Leonardo Fibonacci este considerat un om de știință (pe care l-am menționat deja în articole -,), care a creat baza teoriei lui Eliot.

Cel mai bun broker

Seria digitală a numerelor Fibonacci - raportul de aur și coeficienții sau nivelurile de corecție + video. Numerele Fibonacci în natură.

Specialistul a trăit în secolul al XIII-lea. Omul de știință a publicat o lucrare numită „Cartea calculelor”. Această carte a prezentat Europei o descoperire importantă pentru acele vremuri și nu numai descoperirea - sistemul numeric zecimal. Acest sistem a introdus în circulație numerele obișnuite pentru noi de la zero la nouă.

Apariția acestui sistem a fost prima realizare importantă a Europei de la căderea Romei. Fibonacci a salvat știința numerică pentru Evul Mediu. De asemenea, a pus baze profunde pentru dezvoltarea altor științe, cum ar fi matematica superioară, fizica, astronomia și ingineria mecanică.

Priveste filmarea

Cum au apărut numerele și derivatele lor?

Rezolvând o problemă aplicată, Leonardo a dat peste cap serie curioasă de numere Fibonacci, la începutul căruia sunt două unităţi.

Fiecare termen ulterior este suma celor doi anteriori. Cel mai curios lucru este că seria de numere Fibonacci este o succesiune remarcabilă prin faptul că, dacă împărțiți orice termen la cel anterior, obțineți un număr care este aproape de 0,618. Acest număr a fost numit ratia de aur».

S-a dovedit că acest număr este cunoscut omenirii de foarte mult timp. De exemplu, în Egiptul antic au construit piramide folosindu-l, iar grecii antici și-au construit templele pe el. Leonardo da Vinci a arătat cum structura corpului uman se supune acestui număr.

Natura folosește numerele Fibonacci în zonele ei cele mai intime și avansate. De la structuri atomice și alte forme mici, cum ar fi moleculele de ADN și microcapilarele creierului, până la cele uriașe, cum ar fi orbitele planetare și structurile galaxiilor. Numărul de exemple este atât de mare încât ar trebui argumentat că în natură există într-adevăr o anumită lege de bază a proporțiilor.

Prin urmare, nu este surprinzător că seria Fibonacci și raportul de aur și-au făcut drum spre graficele bursiere. Și nu doar un număr 0,618, ci și derivatele sale.

Dacă ridicați numărul secțiunii de aur la prima, a doua, a treia și a patra putere și scădeți rezultatul din una, atunci obțineți o nouă serie, care se numește " Ratele de retragere Fibonacci". Rămâne doar să adăugați o notă de cinci zecimi - aceasta este cincizeci la sută.

Cu toate acestea, acest lucru nu este tot ce se poate face cu raportul de aur. Dacă împărțim unitatea la 0,618, atunci obținem 1,618, dacă o pătram, atunci obținem 2,618, dacă o ridicăm într-un cub, obținem numărul 4,236. Aceștia sunt coeficienții de expansiune Fibonacci. Singurul lucru care lipsește aici este numărul 3.236, care a fost propus de John Murphy.

Ce cred experții despre secvență?

Unii vor spune că aceste numere sunt deja familiare, deoarece sunt folosite în programele de analiză tehnică pentru a determina cantitatea de corecție și extindere. În plus, aceleași serii joacă un rol important în teoria undelor Eliot. Ele sunt baza sa numerică.

Expertul nostru Nikolay Proven, managerul de portofoliu al companiei de investiții Vostok.

• – Nikolai, ce crezi, este întâmplător apariția numerelor Fibonacci și a derivatelor sale pe diagramele diferitelor instrumente? Și se poate spune: „Aplicația practică a seriei Fibonacci” are loc?
• - Am o atitudine proastă față de misticism. Și cu atât mai mult pe graficele bursiere. Totul are motivele lui. în cartea „Fibonacci Levels” a povestit frumos unde apare raportul de aur, că nu a fost surprins că a apărut pe graficele bursiere. Dar în zadar! Pi apare adesea în multe dintre exemplele pe care le-a dat. Dar din anumite motive nu este în raportul preț.
• - Deci nu crezi în eficacitatea principiului valului Elliot?
• - Nu, nu asta e ideea. Principiul valului este un lucru. Raportul numeric este diferit. Iar motivele apariției lor în graficele de preț sunt al treilea
• – Care credeți că sunt motivele apariției secțiunii de aur în graficele bursiere?
• - Răspunsul corect la această întrebare poate fi în măsură să câștige Premiul Nobel pentru Economie. În timp ce putem ghici adevăratele motive. Ele sunt în mod clar în armonie cu natura. Există multe modele de prețuri de schimb. Ele nu explică fenomenul indicat. Dar neînțelegerea naturii fenomenului nu ar trebui să nege fenomenul ca atare.
• – Și dacă această lege se va deschide vreodată, va putea ea să distrugă procesul de schimb?
• - După cum arată aceeași teorie a valurilor, legea modificării prețurilor acțiunilor este psihologie pură. Mi se pare că cunoașterea acestei legi nu va schimba nimic și nu va putea distruge bursa.

Materialul este furnizat de blogul webmasterului Maxim.

Coincidența fundamentelor principiilor matematicii într-o varietate de teorii pare incredibilă. Poate este fantezie sau o ajustare a rezultatului final. Așteaptă și vezi. O mare parte din ceea ce înainte era considerat neobișnuit sau imposibil: explorarea spațiului, de exemplu, a devenit obișnuită și nu surprinde pe nimeni. De asemenea, teoria undelor, care poate fi de neînțeles, va deveni mai accesibilă și mai înțeleasă cu timpul. Ceea ce era anterior inutil, în mâinile unui analist experimentat, va deveni un instrument puternic pentru prezicerea comportamentului viitor.

Numerele Fibonacci în natură.

Uite

Și acum, să vorbim despre cum puteți respinge faptul că seria digitală Fibonacci este implicată în orice tipare din natură.

Să luăm orice alte două numere și să construim o secvență cu aceeași logică ca și numerele Fibonacci. Adică, următorul membru al secvenței este egal cu suma celor doi anterioare. De exemplu, să luăm două numere: 6 și 51. Acum vom construi o secvență pe care o vom completa cu două numere 1860 și 3009. Rețineți că atunci când împărțim aceste numere, obținem un număr apropiat de raportul de aur.

În același timp, numerele care au fost obținute prin împărțirea altor perechi au scăzut de la prima la ultima, ceea ce ne permite să afirmăm că dacă această serie este continuată la nesfârșit, atunci vom obține un număr egal cu raportul de aur.

Astfel, numerele Fibonacci în sine nu se disting prin nimic. Există și alte secvențe de numere, dintre care există un număr infinit, care au ca rezultat numărul de aur phi ca urmare a acelorași operații.

Fibonacci nu a fost un ezoterist. Nu voia să pună niciun misticism în numere, doar rezolva o problemă obișnuită a iepurilor. Și a scris o secvență de numere care a rezultat din sarcina lui, în prima, a doua și în alte luni, câți iepuri vor fi după reproducere. În decurs de un an, a primit aceeași secvență. Și nu a făcut o relație. Nu a existat nicio proporție de aur, nici o relație divină. Toate acestea au fost inventate după el în Renaștere.

Înainte de matematică, virtuțile lui Fibonacci sunt enorme. A adoptat sistemul de numere de la arabi și a dovedit valabilitatea acestuia. A fost o luptă grea și lungă. Din sistemul numeric roman: greu și incomod pentru numărare. Ea a dispărut după Revoluția Franceză. Nu are nimic de-a face cu secțiunea de aur a lui Fibonacci.

Sunt infinit de multe spirale, cele mai populare sunt: ​​spirala logaritmului natural, spirala lui Arhimede, spirala hiperbolica.

Împreună cu editura „” publicăm un fragment din cartea profesorului de matematică aplicată Edward Sheinerman „Ghid pentru iubitorii de matematică”, dedicat problemelor non-standard de matematică fascinantă, puzzle-uri, Universul numerelor și cifrelor. Traducere din engleză de Alexey Ognev.

Acest capitol vorbește despre celebrele numere Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21 etc. Această serie a fost numită după Leonardo din Pisa, mai cunoscut sub numele de Fibonacci. Leonardo din Pisa (1170–1250) - unul dintre primii matematicieni majori din Europa medievală Porecla Fibonacci înseamnă „fiul lui Bonacci”. Autor al Cărții Abacului, care conturează sistemul numeric zecimal.

Pătrate și domino

Să începem prin a așeza pătrate și domino. Imaginați-vă un cadru orizontal lung de 1 × 10. Vrem să îl umplem complet cu pătrate de 1 × 1 și piese de domino 1 × 2, fără a lăsa goluri. Iată poza:

Întrebare: În câte moduri se poate face acest lucru?

Pentru comoditate, notăm numărul de opțiuni cu F10. Să le parcurgem pe toate și apoi să le recalculezi este o muncă grea, plină de erori. Mult mai bine pentru a simplifica sarcina. Să nu căutăm imediat F10, să începem cu F1. Este mai ușor ca niciodată! Trebuie să umplem un cadru 1 × 1 cu pătrate 1 × 1 și domino 1 × 2. Dominourile nu se potrivesc, rămâne singura soluție: luați un pătrat. Cu alte cuvinte, F1 = 1.

Acum să ne ocupăm de F2. Dimensiunea cadrului este de 1 × 2. Îl puteți umple cu două pătrate sau un domino. Deci există două opțiuni și F2 = 2.

Următorul: În câte moduri poate fi umplut un cadru 1 × 3? Prima opțiune: trei pătrate. Alte două opțiuni: un domino (două nu se potrivesc) și un pătrat în stânga sau în dreapta. Deci, F3 = 3. Încă un pas: luați un cadru de 1 × 4. Figura arată toate opțiunile de umplere:

Am găsit cinci posibilități, dar care este garanția că nu am omis nimic? Există o modalitate de a te testa. La capătul din stânga cadrului poate fi fie un pătrat, fie un domino. În rândul de sus din imagine - opțiuni când pătratul este în stânga, în rândul de jos - când domino sunt în stânga.

Să presupunem că este un pătrat în stânga. Restul trebuie umplut cu pătrate și domino. Cu alte cuvinte, trebuie să completați caseta 1 × 3. Acest lucru oferă 3 opțiuni, deoarece F3 = 3. Dacă există piese de domino în stânga, dimensiunea părții rămase este 1 × 2 și există două opțiuni de completat aceasta, deoarece F2 = 2.

Deci avem 3 + 2 = 5 opțiuni și ne-am asigurat că F4 = 5.

Acum tu. Gândiți-vă câteva minute și găsiți toate opțiunile de umplere pentru cadrul 1 × 5. Nu sunt multe dintre ele. Soluția este la sfârșitul capitolului. Te poți relaxa și gândi.

Să revenim la pătratele noastre. Aș vrea să cred că ați găsit 8 opțiuni, deoarece există 5 moduri de așezare, unde pătratul este în stânga și încă 3 moduri, unde piesele de domino sunt în stânga. Deci F5 = 8.

Să rezumam. Am etichetat FN numărul de moduri de a umple un cadru de 1 × n cu pătrate și piese de domino. Trebuie să găsim F10. Iată ce știm deja:

Mergem mai departe. Cu ce ​​este egal F6? Puteți desena toate opțiunile, dar este plictisitor. Să împărțim întrebarea în două părți. În câte moduri poate fi completat un cadru de 1 × 6 dacă în stânga este (a) un pătrat și (b) un domino? Vestea bună este că știm deja răspunsul! În primul caz, rămânem cu cinci pătrate și știm că F5 = 8. În al doilea caz, trebuie să umplem patru pătrate; știm că F4 = 5. Deci F5 + F4 = 13.

Cu ce ​​este egal F7? Pe baza acelorași considerații, F7 = F6 + F5 = 13 + 8 = 21. Dar F8? Evident F8 = F7 + F6 = 21 + 13 = 34. Și așa mai departe. Am găsit următoarea relație: Fn = Fn-1 + Fn-2.

Încă câțiva pași - și vom găsi numărul dorit F10. Răspunsul corect este la sfârșitul capitolului.

numerele Fibonacci

Numerele Fibonacci sunt succesiunea:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …

Este construit după următoarele reguli:

— primele două numere 1 și 1;

— fiecare număr următor se obține prin adunarea celor două anterioare.

Vom nota al n-lea element al secvenței Fn, începând de la zero: F0 = 1, F1 = 1, F2 = 2, F3 = 3, F4 = 5, ... Calculăm următorul element prin formula: Fn = Fn-1 + Fn-2.

După cum putem vedea, problema stivuirii pătratelor și a pieselor de domino ne-a condus la succesiunea numerelor Fibonacci [ 1 ]În problema pătratelor și dominoului, am aflat: F1 = 1 și F2 = 2. Dar numerele Fibonacci încep cu F0 = 1. Cum se potrivește acest lucru cu condițiile problemei? Câte moduri există de a umple cadrul 0 × 1 în aceleași condiții? Lungimea pătratului și lungimea dominoului sunt ambele mai mari decât zero, așa că există tentația de a spune că răspunsul este zero, dar nu este. Dreptunghiul 0 × 1 este deja umplut, nu există sloturi; nu avem nevoie de un pătrat sau un domino. Astfel, există un singur curs de acțiune: nu luați un pătrat sau domino. Înțelegi? În acest caz, felicitări. Ai un suflet de matematician!

Suma numerelor Fibonacci

Să încercăm să adăugăm primele câteva numere Fibonacci. Ce putem spune despre suma F0 + F1 +... + Fn pentru orice n? Hai să facem niște calcule și să vedem ce se întâmplă. Observați rezultatele adăugării de mai jos. Vedeți un model? Așteptați puțin înainte de a trece mai departe: este mai bine dacă găsiți singur răspunsul, decât să citiți o soluție gata făcută.

Aș vrea să cred că ați văzut că rezultatele însumării, dacă li se adaugă una, se aliniază și ele într-o succesiune de numere Fibonacci. De exemplu, adăugarea numerelor F0 la F5 dă: F0 + F1 + F2 + F3 + F4 + F5 = 1 + 1 + 2 + 3 + 5 + 8 = 20 = F7 - 1. Adăugarea numerelor F0 la F6 dă 33, care este cu unu mai puțin decât F8 = 34. Putem scrie formula pentru numere întregi nenegative n: F0 +F1 +F2 +…+Fn =Fn+2 –1. (*)

Probabil că va fi suficient pentru dvs. personal să vedeți că formula [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1.. lucrează într-o duzină de cazuri pentru a te face să crezi că este adevărat, dar matematicienii sunt înfometați de dovezi. Suntem bucuroși să vă prezentăm două dovezi posibile că este adevărat pentru toate numerele întregi nenegative n.

Prima se numește demonstrație prin inducție, a doua se numește demonstrație combinatorie.

Dovada prin inducție

Formulă [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. este un număr infinit de formule în formă pliată. Demonstrează că [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. adevărat pentru o anumită valoare a lui n, să spunem pentru n = 6, este o problemă aritmetică simplă. Va fi suficient să scrieți numerele de la F0 la F6 și să le adăugați: F0 + F2 + ... + F6 = 1 + 1 + 2 + 3 + 5 + 8 + 13 = 33.

Este ușor de observat că F8 = 34, deci formula funcționează. Să trecem la F7. Să nu pierdem timpul și să adunăm toate numerele: știm deja suma până la F6. Astfel, (F0 +F1 +…+F6)+F7 =33+21=54. Ca și înainte, totul converge: F9 = 55.

Dacă acum începem să verificăm dacă formula pentru n = 8 funcționează, puterea noastră se va epuiza în sfârșit. Dar totuși, să vedem ce știm deja și ce vrem să aflăm:

F0 +F1 +…+F7 =F9.

F0 +F1 +…+F7 +F7 =?

Să folosim rezultatul anterior: (F0 +F1 +…+F7)+F8 =(F9-1)+F8.

Desigur, putem calcula (F9-1) + F8 aritmetic. Dar asta ne va obosi și mai mult. În același timp, știm că F8 + F9 = F10. Astfel, nu trebuie să calculăm nimic sau să ne uităm în tabelul numerelor Fibonacci:

(F0 + F1 +... + F7) + F8 = (F9-1) + F8 = (F8 + F9-1) = F10-1.

Am verificat că formula funcționează pentru n = 8 pe baza a ceea ce știam despre n = 7.

În cazul lui n = 9, ne bazăm pe rezultatul pentru n = 8 în același mod (vedeți singuri). Desigur, dovedind corectitudinea [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. pentru n, putem fi siguri că [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. adevărat și pentru n + 1.

Suntem gata să dăm o dovadă completă. După cum sa menționat deja, [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. reprezintă un număr infinit de formule pentru toate valorile lui n de la zero la infinit. Să vedem cum funcționează dovada.

Mai întâi demonstrăm [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1.în cel mai simplu caz, pentru n = 0. Verificăm pur și simplu că F0 = F0+2 - 1. Deoarece F0 = 1 și F2 = 2, evident 1 = 2 - 1 și F0 = F2-1.

În plus, este suficient să arătăm că corectitudinea formulei pentru o valoare a lui n (să zicem, n = k) înseamnă automat corectitudinea pentru n + 1 (în exemplul nostru, n = k + 1). Trebuie doar să demonstrăm cum funcționează „automat”. Ce trebuie să facem?

Să luăm un număr k. Să presupunem că știm deja că F0+F1+…+Fk =Fk+2–1. Căutăm valoarea F0 + F1 +... + Fk + Fk+1.

Știm deja suma numerelor Fibonacci până la Fk, așa că obținem:

(F0+F1+…+Fk)+Fk+1 =(Fk+2–1)+Fk+1.

Partea dreaptă este egală cu Fk+2 - 1 + Fk+1 și știm cu ce este egală suma numerelor Fibonacci consecutive:

Fk+2–1 + Fk+1 = (Fk+2 + Fk+1) - 1 = Fk+3– 1

Înlocuiți în ecuația noastră:

(F0+F1+…+Fk)+Fk+1 =Fk+3–1

Acum voi explica ce am făcut. Dacă știm că [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. este adevărată când însumăm numerele la Fk, atunci [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. ar trebui să fie adevărat dacă adăugăm Fk+1.

A rezuma:

Formulă [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. adevărat pentru n = 0.

Dacă formula [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. este adevărat pentru n, este adevărat și pentru n + 1.

Putem spune cu încredere că [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. este valabilă pentru orice valoare a lui n. Este adevarat [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. pentru n=4987? Acest lucru este adevărat dacă expresia este adevărată pentru n = 4986, care se bazează pe faptul că expresia este adevărată pentru n = 4985 și așa mai departe până la n = 0. Prin urmare, formula [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. este valabil pentru toate valorile posibile. Această metodă de probă este cunoscută ca inducție matematică (sau demonstrație prin inducție). Verificăm cazul de bază și dăm un șablon prin care fiecare caz următor poate fi dovedit pe baza celui precedent.

Dovada combinatorie

Și iată o cu totul altă dovadă a identității [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1.. Abordarea principală aici este de a profita de faptul că numărul Fn este numărul de moduri de a acoperi un dreptunghi 1 × n cu pătrate și domino.

Permiteți-mi să vă reamintesc că trebuie să dovedim:

F0 + F1 + F2 +… + Fn = Fn+2- 1. (*)

Ideea este de a trata ambele părți ale ecuației ca o soluție la problema de placare. Dacă demonstrăm că părțile din stânga și din dreapta sunt soluția pentru același dreptunghi, acestea vor coincide una cu cealaltă. Această tehnică se numește demonstrație combinatorie[ 2 ]Cuvântul „combinatorial” este derivat din substantivul „combinatorial” - numele ramului matematicii, al cărei subiect este calculul opțiunilor în probleme similare cu acoperirea unui dreptunghi. Cuvântul „combinatoric”, la rândul său, este derivat din cuvântul „combinații”..

Ce întrebare în combinatorică este ecuația [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. da doua raspunsuri corecte? Acest puzzle este similar cu cele găsite în emisiunea Jeopardy! [ 3 ]O emisiune TV populară în SUA. Similar cu Jeopardy! publicate în diferite țări; în Rusia este „Joc propriu”. - Aprox. ed., unde participanții trebuie să formuleze o întrebare, cunoscând în prealabil răspunsul corect.

Partea dreaptă pare mai simplă, așa că să începem cu ea. Răspuns: Fn+2– 1. Care este întrebarea? Dacă răspunsul ar fi simplu Fn+2, am putea formula cu ușurință întrebarea: în câte moduri poate fi placat un dreptunghi 1 × (n + 2) cu pătrate și domino? Acesta este aproape exact ceea ce aveți nevoie, dar răspunsul este mai puțin de unul. Să încercăm să schimbăm ușor întrebarea și să reducem răspunsul. Să eliminăm o versiune a căptușelii și să recalculăm restul. Dificultatea este să găsești o opțiune care să fie radical diferită de restul. Există unul?

Fiecare metodă de placare implică utilizarea pătratelor sau a pieselor de domino. Doar pătratele sunt implicate în singura variantă, în celelalte există cel puțin un domino. Să luăm asta drept baza unei noi întrebări.

Întrebare: Câte opțiuni există pentru acoperirea unui cadru dreptunghiular de 1 × (n + 2) cu pătrate și domino, inclusiv cel puțin un domino?

Acum vom găsi două răspunsuri la această întrebare. Deoarece ambele vor fi adevărate, între numere putem pune cu încredere un semn egal.

Am discutat deja unul dintre răspunsuri. Există opțiuni de stivuire Fn+2. Doar unul dintre ele presupune utilizarea exclusivă a pătratelor, fără domino. Astfel, răspunsul #1 la întrebarea noastră este: Fn+2– 1.

Al doilea răspuns ar trebui să fie - sper - partea stângă a ecuației [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1.. Să vedem cum funcționează.

Este necesar să se recalculeze opțiunile de umplere a cadrului, inclusiv cel puțin un domino. Să ne gândim unde va fi localizat primul os. Există n + 2 poziții, iar prima piesă poate fi în pozițiile de la 1 la n + 1.

Luați în considerare cazul n = 4. Căutăm modalități de a umple un cadru de 1 × 6 care implică cel puțin un domino. Știm răspunsul: F6 - 1 = 13 - 1 = 12, dar trebuie să-l obținem într-un mod diferit.

Primul domino poate lua următoarele poziții:

Prima coloană arată cazul când articulația este în prima poziție, a doua - când articulația este în a doua poziție și așa mai departe.

Câte opțiuni sunt în fiecare coloană?

Prima coloană conține cinci opțiuni. Dacă aruncăm piesele de domino din stânga, obținem exact F4 = 5 opțiuni pentru un dreptunghi de 1 × 4. În a doua coloană, există trei opțiuni. Să lăsăm piesele de domino și pătratul din stânga. Obținem F3 = 3 opțiuni pentru un dreptunghi de 1 × 3. La fel și pentru celelalte coloane. Iată ce am găsit:

Astfel, numărul de moduri de a plasa pătrate și domino (cel puțin un os) pe un cadru dreptunghiular de 1 × 6 este F4 + F3 + F2 + F1 + F0 = 12.

Ieșire: F0+F1+F2+F3+F4=12=F6–1.

Să luăm în considerare cazul general. Ni se dă un cadru de lungime n + 2. Câte moduri există pentru a-l umple, în care primul domino se află într-o poziție k? În acest caz, primele k - 1 poziții sunt ocupate de pătrate. Astfel, k + 1 poziții sunt ocupate în total [ 4 ]Numărul k poate lua valori de la 1 la n + 1, dar nu mai mult, pentru că, altfel, ultimul domino va ieși din cadru.. Restul (n + 2) - (k + 1) = n - k + 1 poate fi completat prin orice mijloace. Acest lucru oferă opțiuni Fn-k+1. Să construim o diagramă:

Dacă k se modifică de la 1 la n + 1, valoarea lui n - k + 1 se schimbă de la 0 la n. Astfel, numărul de opțiuni pentru umplerea cadrului nostru cu cel puțin un domino este Fn + Fn-1 +... + F1 + F0.

Dacă punem termenii în ordine inversă, obținem partea stângă a expresiei (*). Astfel, am găsit al doilea răspuns la întrebarea pusă: F0 +F1 +…+Fn.

Deci avem două răspunsuri la întrebare. Valorile obținute cu ajutorul celor două formule pe care le-am derivat coincid, iar identitatea [ * ]F0 +F1 +F2 +…+Fn =Fn+2 –1. dovedit.

Raportul Fibonacci și raportul de aur

Adunarea a două numere Fibonacci succesive dă următorul număr Fibonacci. În această secțiune, vom atinge o întrebare mai interesantă: ce se întâmplă dacă împărțim numărul Fibonacci la cel care îl precede în serie? Să calculăm raportul Fk1. Pentru valori crescătoare ale lui k.

În tabel puteți vedea rapoartele de la F1/F0 la F20/19.

Cu cât numerele Fibonacci devin mai mari, cu atât raportul Fk+1/Fk este mai aproape de o constantă aproximativ egală cu 1,61803. Acest număr este - veți fi surprins - binecunoscut, iar dacă îl introduceți într-un motor de căutare, o mulțime de pagini despre raportul de aur vor cădea. Ce este? Raportul numerelor Fibonacci vecine nu este același. Cu toate acestea, este aproape la fel dacă numerele sunt suficient de mari. Să găsim o formulă pentru numărul 1,61803 și pentru aceasta vom presupune pentru o vreme că toate rapoartele sunt aceleași. Introducem notatia x:

x=Fk+1/ Fk=/ Fk+2/ Fk+1= Fk+3/ Fk+2=…

Aceasta înseamnă că Fk+1 = xFk, Fk+2 = xFk+1 etc. Putem reformula:

Fk+2=xFk+1=x2>Fk.

Dar știm că Fk+2= Fk+1 + Fk. Astfel, x2>FkFk = xFk + Fk.

Dacă împărțim ambele părți cu Fk și rearanjam termenii, obținem o ecuație pătratică: x2-x-1=0. Are doua solutii:

Raportul trebuie să fie pozitiv. Și așa am primit numărul pe care îl cunoaștem. De obicei, litera greacă φ (phi) este folosită pentru a desemna raportul de aur:

Am observat deja că raportul numerelor Fibonacci vecine se apropie (tinde) de φ. Acest lucru este uimitor. Acest lucru ne oferă o altă modalitate de a calcula numerele Fibonacci aproximative. Sirul numerelor Fibonacci este seria F0 F1, F2, F3, F4, F5... Dacă toate rapoartele Fk+1/Fk sunt aceleași, obținem formula:

Aici Cu este o altă constantă. Să comparăm valorile rotunjite ale lui Fn și φn pentru n diferit:

Pentru valori mari ale lui n, raportul Fn/φn≈0,723607. Acest număr este exact φ/rădăcină5. Cu alte cuvinte,

Rețineți că dacă rotunjim la cel mai apropiat număr întreg, obținem exact Fn.

Dacă nu doriți să vă deranjați cu rotunjirea la un număr întreg, atunci formula numită după Jacques Binet [ 5 ]Jacques Binet (1786–1856) - matematician, mecanic și astronom francez Formula numerelor Fibonacci poartă numele lui Binet, deși Abraham de Moivre (1667–1754) o derivase cu aproape o sută de ani mai devreme. - Aprox. pe., vă va oferi valoarea exactă:

Umpleți cadru 1×5

Cadrul nostru poate fi umplut cu pătrate și piese de domino în următoarele moduri:

Există F4 = 5 opțiuni când există un pătrat la început și F3 = 3 opțiuni când există un domino la început. În total, acest lucru oferă F5 = F4 + F3 = 8 opțiuni.

valoarea F10(răspunsul la următoarea întrebare despre stil) este 89.

Cu ceva timp în urmă, am promis să comentez afirmația lui Tolkaciov că Sankt Petersburg a fost construit conform principiului Secțiunii de Aur, iar Moscova - conform principiului simetriei și că de aceea diferențele de percepție a acestor două orașe sunt atât de palpabile, și de aceea un Sf.”, Și moscovitul „se îmbolnăvește cu capul” când vine la Sankt Petersburg. Este nevoie de ceva timp pentru a te adapta la oraș (ca atunci când zbori în state - trebuie să te adaptezi în timp).

Faptul este că ochiul nostru arată - simțind spațiul cu ajutorul anumitor mișcări ale ochilor - sacade (în traducere - bataie de vele). Ochiul face un „pop” și trimite un semnal creierului „a avut loc aderența la suprafață. Totul e bine. Aceasta este o informație.” Și în timpul vieții ochiului se obișnuiește cu un anumit ritm al acestor sacade. Iar atunci când acest ritm se schimbă drastic (de la peisajul urban la pădure, de la Secțiunea de Aur la simetrie), atunci este nevoie de ceva muncă a creierului pentru reconfigurare.

Acum detaliile:
Definiția ZS este împărțirea unui segment în două părți într-un astfel de raport încât partea mai mare să fie legată de cea mai mică, întrucât suma lor (întregul segment) este cu cea mai mare.

Adică, dacă luăm întregul segment c ca 1, atunci segmentul a va fi egal cu 0,618, segmentul b - 0,382. Astfel, dacă luăm o clădire, de exemplu, un templu construit conform principiului GS, atunci cu înălțimea sa, să zicem, 10 metri, înălțimea tamburului cu domul va fi de 3,82 cm, iar înălțimea bazei a cladirii va avea 6,18 cm.(Este clar ca numerele pe care le-am luat sunt egale pentru claritate)

Și care este relația dintre numerele GL și Fibonacci?

Numerele de ordine Fibonacci sunt:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…

Modelul numerelor este că fiecare număr următor este egal cu suma celor două numere anterioare.
0 + 1 = 1;
1 + 1 = 2;
2 + 3 = 5;
3 + 5 = 8;
5 + 8 = 13;
8 + 13 = 21 etc.

iar raportul numerelor adiacente se apropie de raportul lui 3S.
Deci, 21:34 = 0,617 și 34:55 = 0,618.

Adică, în centrul ZS se află numerele șirului Fibonacci.
Acest videoclip demonstrează din nou clar această legătură între AP și numerele Fibonacci

Unde se mai întâlnesc principiul AP și numerele de succesiune Fibonacci?

Frunzele plantelor sunt descrise de succesiunea Fibonacci. Semințele de floarea soarelui, conurile de pin, petalele de flori, celulele de ananas sunt de asemenea aranjate după succesiunea Fibonacci.

ou de pasăre

Lungimile falangelor degetelor umane sunt aproximativ aceleași cu numerele Fibonacci. Raportul de aur se vede în proporțiile feței.

Emil Rozenov a studiat ZS în muzica epocii baroc și clasicism folosind lucrările lui Bach, Mozart, Beethoven ca exemplu.

Se știe că Serghei Eisenstein a construit artificial filmul „Cuirasatul Potemkin” conform regulilor Adunării Legislative. A spart banda în cinci părți. În primele trei, acțiunea se dezvoltă pe navă. În ultimele două - la Odesa, unde se desfășoară răscoala. Această tranziție către oraș are loc exact în punctul raportului de aur. Da, și în fiecare parte există un punct de cotitură, care are loc conform legii secțiunii de aur. În cadru, scenă, episod, există un anumit salt în dezvoltarea temei: intriga, starea de spirit. Eisenstein credea că, deoarece o astfel de tranziție este aproape de punctul de secțiune de aur, este percepută ca fiind cea mai naturală și naturală.

Multe elemente decorative, precum și fonturi, sunt create folosind GS. De exemplu, fontul lui A. Dürer (litera „A” din figură)

Se crede că termenul „Proporția de Aur” a fost introdus de Leonardo Da Vinci, care spunea „Nimeni care nu este matematician să nu îndrăznească să-mi citească lucrările” și a arătat proporțiile corpului uman în faimosul său desen „Omul de Vitruvian”. ". „Dacă legăm o figură umană – cea mai perfectă creație a Universului – cu o centură și apoi măsurăm distanța de la centură la picioare, atunci această valoare se va referi la distanța de la aceeași centură până la vârful capului, ca toată înălțimea unei persoane până la lungimea de la centură până la picioare.”

Celebrul portret al Monei Lisa sau Gioconda (1503) a fost creat pe principiul triunghiurilor de aur.

Strict vorbind, steaua în sine sau pentacolul este construcția AP.

O serie de numere Fibonacci este modelată vizual (materializată) sub forma unei spirale

Și în natură, spirala 3S arată astfel:

În același timp, spirala este observată peste tot(în natură și nu numai):
- Semințele la majoritatea plantelor sunt aranjate în spirală
- Un păianjen țese o pânză în spirală
- Un uragan curge în spirală
- O turmă speriată de reni se împrăștie în spirală.
- Molecula de ADN este răsucită într-o dublă spirală. Molecula de ADN este formată din două elice împletite vertical, lungi de 34 de angstromi și lățime de 21 de angstromi. Numerele 21 și 34 se succed în succesiunea lui Fibonacci.
- Embrionul se dezvolta sub forma unei spirale
- spirală „cohleea în urechea internă”
- Apa coboară prin scurgere în spirală
- Dinamica spirală arată dezvoltarea personalității unei persoane și a valorilor sale într-o spirală.
- Și, desigur, Galaxia în sine are forma unei spirale

Astfel, se poate susține că natura însăși este construită pe principiul Secțiunii de Aur, motiv pentru care această proporție este percepută mai armonios de ochiul uman. Nu necesită „reparare” sau completare a imaginii rezultate din lume.

Acum despre secțiunea de aur în arhitectură

Piramida lui Keops reprezintă proporțiile GS. (Imi place fotografia - cu Sfinxul presărat cu nisip).

Potrivit lui Le Corbusier, în relieful din templul faraonului Seti I de la Abydos și în relieful care îl înfățișează pe faraonul Ramses, proporțiile figurilor corespund raportului de aur. Fațada templului antic grecesc al Partenonului are și proporții aurii.

Catedrala Notredam de Paris din Paris, Franța.

Una dintre clădirile remarcabile realizate după principiul AP este Catedrala Smolny din Sankt Petersburg. Două poteci duc la catedrală de-a lungul marginilor, iar dacă te apropii de catedrală de-a lungul lor, atunci parcă se ridică în aer.

La Moscova, există și clădiri realizate folosind ZS. De exemplu, Catedrala Sf. Vasile

Cu toate acestea, predomină clădirile care folosesc principiile simetriei.
De exemplu, Kremlinul și Turnul Spasskaya.

De asemenea, înălțimea zidurilor Kremlinului nu reflectă nicăieri principiul AP privind înălțimea turnurilor, de exemplu. Sau luați hotelul Rusia, sau hotelul Cosmos.

În același timp, clădirile construite după principiul AP reprezintă un procent mai mare în Sankt Petersburg, în timp ce acestea sunt clădiri stradale. Bulevardul Liteiny.

Astfel, Raportul de Aur folosește un raport de 1,68, iar simetria este 50/50.
Adică, clădirile simetrice sunt construite pe principiul egalității laturilor.

O altă caracteristică importantă a GS este dinamismul său și dorința de a se desfășura, datorită succesiunii numerelor Fibonacci. În timp ce simetria, dimpotrivă, reprezintă stabilitate, stabilitate și imobilitate.

În plus, ZS suplimentară introduce o abundență de spații de apă în planul lui Peter, revărsându-se peste oraș și dictând subordonarea orașului în curbele lor. Și schema lui Peter în sine seamănă cu o spirală sau cu un embrion în același timp.

Papa, însă, a exprimat o versiune diferită a motivului pentru care moscoviții și locuitorii Sankt-Petersburgului au „dureri de cap” atunci când vizitează capitalele. Papa raportează acest lucru la energiile orașelor:
Sankt Petersburg - are un gen masculin și, în consecință, energii masculine,
Ei bine, Moscova, respectiv, este feminină și are energii feminine.

Așadar, locuitorii capitalelor, care s-au adaptat la echilibrul lor de feminin și masculin în corpul lor, le este greu să se reconstruiască atunci când vizitează un oraș învecinat, iar cineva poate avea unele dificultăți cu perceperea uneia sau alteia energie și prin urmare, orașul vecin s-ar putea să nu fie deloc îndrăgostit!

Această versiune este susținută de faptul că toate împărăteașele ruse au condus la Sankt Petersburg, în timp ce Moscova a văzut doar țari bărbați!

Resurse folosite.

Leonardo de Pisa (lat. Leonardus Pisanus, italian. Leonardo Pisano, în jurul anului 1170, Pisa - în jurul anului 1250, ibid) - primul mare matematician al Europei medievale. Cel mai cunoscut sub numele de Fibonacci.
Citiți mai multe aici: http://ru.wikipedia.org/wiki/%D4%E8%E1%EE%ED%E0%F7%F7%E8

Secvența Fibonacci, cunoscută de toată lumea din filmul Codul lui Da Vinci, este o serie de numere descrise ca o ghicitoare de către matematicianul italian Leonardo din Pisa, mai cunoscut sub numele de Fibonacci, în secolul al XIII-lea. Pe scurt, esența ghicitorii:

Cineva a plasat o pereche de iepuri într-un anumit spațiu închis pentru a afla câte perechi de iepuri s-ar fi născut în cursul anului, dacă natura iepurilor este de așa natură încât în ​​fiecare lună o pereche de iepuri produce o altă pereche și capacitatea de a produce puii apare la vârsta de două luni.

Secvența Fibonacci și Iepuri
Rezultatul este următoarea serie de numere: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, unde numărul de perechi de iepuri din fiecare dintre cele douăsprezece luni este afișat separat de virgule. Poate fi continuat pe termen nelimitat. Esența sa este că fiecare număr următor este suma celor două precedente.

Această serie are mai multe caracteristici matematice care trebuie atinse. Asimptotic (apropiindu-se din ce în ce mai încet) tinde spre un raport constant. Cu toate acestea, acest raport este irațional, adică este un număr cu o succesiune infinită, imprevizibilă de cifre zecimale în partea fracțională. Nu poate fi exprimat exact.

Deci raportul oricărui membru al seriei față de cel precedent fluctuează în jurul numărului 1.618, uneori depășindu-l, alteori neatingându-l. Raportul la următorul se apropie în mod similar de numărul 0,618, care este invers proporțional cu 1,618. Dacă împărțim elementele într-un singur element, vom obține numerele 2,618 și 0,382, care sunt, de asemenea, invers proporționale. Acestea sunt așa-numitele rapoarte Fibonacci.

De ce toate astea?

Așa că ne apropiem de unul dintre cele mai misterioase fenomene ale naturii. Intelegetul Leonardo, de fapt, nu a descoperit nimic nou, pur și simplu a reamintit lumii un astfel de fenomen precum Secțiunea de Aur, care nu este inferioară ca importanță teoremei lui Pitagora.

Distingem toate obiectele din jurul nostru, inclusiv prin formă. Unele ne plac mai mult, altele mai puțin, altele resping complet privirea. Uneori interesul poate fi dictat de o situație de viață, iar uneori de frumusețea obiectului observat. Forma simetrică și proporțională contribuie la cea mai bună percepție vizuală și evocă un sentiment de frumusețe și armonie. O imagine holistică constă întotdeauna din părți de dimensiuni diferite, care se află într-o anumită relație între ele și întregul. Raportul de aur este cea mai înaltă manifestare a perfecțiunii întregului și a părților sale în știință, artă și natură.

Dacă pe un exemplu simplu, atunci Secțiunea de Aur este împărțirea unui segment în două părți într-un astfel de raport în care partea mai mare se raportează la cea mai mică, ca suma lor (întregul segment) la cea mai mare.

Secțiunea de Aur - Decupat
Dacă luăm ca 1 întregul segment c, atunci segmentul a va fi egal cu 0,618, segmentul b - 0,382, doar astfel se va îndeplini condiția Secțiunii de Aur (0,618/0,382=1,618; 1/0,618=1,618). Raportul dintre c la a este 1,618 și c la b este 2,618. Aceștia sunt toți la fel, deja familiari nouă, coeficienți Fibonacci.

Desigur, există un dreptunghi auriu, un triunghi auriu și chiar un cuboid auriu. Proporțiile corpului uman în multe privințe sunt apropiate de Secțiunea de Aur.

Raportul de aur și corpul uman


Imagine: marcus-frings.de

Secvența Fibonacci - Animație

Dar cel mai interesant începe atunci când combinăm cunoștințele acumulate. Figura arată clar relația dintre succesiunea Fibonacci și raportul de aur. Începem cu două pătrate de prima dimensiune. De sus adăugăm un pătrat de a doua dimensiune. Pictam langa un patrat cu latura egala cu suma laturilor celor doua anterioare, a treia dimensiune. Prin analogie, apare un pătrat de dimensiunea a cincea. Și așa mai departe până te plictisești, principalul lucru este că lungimea laturii fiecărui pătrat următor este egală cu suma lungimilor laturilor celor două anterioare. Vedem o serie de dreptunghiuri ale căror laturi sunt numere Fibonacci și, în mod ciudat, sunt numite dreptunghiuri Fibonacci.

Dacă tragem o linie netedă prin colțurile pătratelor noastre, nu obținem nimic mai mult decât o spirală a lui Arhimede, a cărei creștere a pasului este întotdeauna uniformă.

Spirala Fibonacci

Nu-ți aduce aminte de nimic?

Credit foto: ethanhein pe Flickr

Și nu numai în coaja unei moluște puteți găsi spiralele lui Arhimede, dar în multe flori și plante, pur și simplu nu sunt atât de evidente.

Aloe multifrunze:


Foto: brewbooks pe Flickr

Broccoli Romanesco:


Foto: beart.org.uk

floarea soarelui:


Foto: esdrascalderan pe Flickr

Con de brad:


Fotografie: manj98 pe Flickr

Și atunci este timpul să ne amintim de Secțiunea de Aur! Este vreuna dintre cele mai frumoase și armonioase creații ale naturii descrise în aceste fotografii? Și asta nu este tot. Privind atent, puteți găsi modele similare în multe forme.

Desigur, afirmația că toate aceste fenomene sunt construite pe secvența Fibonacci sună prea tare, dar tendința este pe față. Și în plus, ea însăși este departe de a fi perfectă, ca orice altceva pe lumea asta.

Există speculații că seria Fibonacci este încercarea naturii de a se adapta la o secvență logaritmică de secțiune de aur mai fundamentală și mai perfectă, care este practic aceeași, pur și simplu începe de nicăieri și nu merge nicăieri. Natura, pe de altă parte, are nevoie cu siguranță de un fel de început întreg, de la care să te poți împinge, nu poate crea ceva din nimic. Rapoartele primilor membri ai șirului Fibonacci sunt departe de Secțiunea de Aur. Dar cu cât ne deplasăm mai departe, cu atât aceste abateri sunt mai netezite. Pentru a determina orice serie, este suficient să cunoști trei dintre membrii ei, mergând unul după altul. Dar nu pentru șirul de aur, două sunt suficiente pentru aceasta, este o progresie geometrică și aritmetică în același timp. Ai putea crede că aceasta este baza pentru toate celelalte secvențe.

Fiecare membru al secvenței logaritmice de aur este un grad al raportului de aur (z). O parte a rândului arată cam așa: ... z-5; z-4; z-3; z-2; z-1; z0; z1; z2; z3; z4; z5 ... Dacă rotunjim valoarea raportului de aur la trei zecimale, obținem z=1,618, atunci seria arată astfel: ... 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 ... Fiecare termen următor poate fi obținut nu numai prin înmulțirea celui precedent cu 1,618, ci și prin adunarea celor doi anteriori. Astfel, creșterea exponențială se realizează prin simpla adăugare a două elemente învecinate. Aceasta este o serie fără început și sfârșit și tocmai aceasta încearcă să fie șirul Fibonacci. Având un început bine definit, se străduiește spre ideal, neatingând niciodată. Asta-i viata.

Și totuși, în legătură cu tot ceea ce se vede și se citește, apar întrebări destul de firești:
De unde au venit aceste cifre? Cine este acest arhitect al universului care a încercat să-l facă perfect? A fost vreodată așa cum și-a dorit el să fie? Și dacă da, de ce a eșuat? Mutații? Alegere libera? Ce va urma? Bobina se răsucește sau se desface?

Găsind răspunsul la o întrebare, obțineți următoarea. Dacă o rezolvi, primești două noi. Tratează-te cu ei, vor apărea încă trei. După ce le-ai rezolvat, vei dobândi cinci nerezolvate. Apoi opt, apoi treisprezece, 21, 34, 55...