Acasă » clasa a 5-a » Linia mediană a unui trapez este egală cu baza acestuia. Cum să găsiți linia mediană a unui trapez. Sarcina de revizuire

Linia mediană a unui trapez este egală cu baza acestuia. Cum să găsiți linia mediană a unui trapez. Sarcina de revizuire

Conceptul liniei mediane a trapezului

În primul rând, să ne amintim ce fel de figură se numește trapez.

Definiția 1

Un trapez este un patrulater în care două laturi sunt paralele, iar celelalte două nu sunt paralele.

În acest caz, laturile paralele se numesc bazele trapezului, iar laturile neparalele se numesc laturile laterale ale trapezului.

Definiția 2

Linia mediană a unui trapez este un segment care leagă punctele medii ale laturilor laterale ale trapezului.

Teorema liniei mediane a trapezului

Acum introducem teorema despre linia mediană a unui trapez și o demonstrăm folosind metoda vectorială.

Teorema 1

Linia mediană a trapezului este paralelă cu bazele și egală cu jumătatea sumei acestora.

Dovada.

Să ni se dea un trapez $ABCD$ cu bazele $AD\ și\ BC$. Și să fie $MN$ linia de mijloc a acestui trapez (Fig. 1).

Figura 1. Linia mediană a trapezului

Să demonstrăm că $MN||AD\ și\ MN=\frac(AD+BC)(2)$.

Luați în considerare vectorul $\overrightarrow(MN)$. Apoi folosim regula poligonului pentru a adăuga vectori. Pe de o parte, înțelegem asta

Pe cealaltă parte

Să adunăm ultimele două egalități și să obținem

Deoarece $M$ și $N$ sunt punctele medii ale laturilor laterale ale trapezului, vom avea

Primim:

Prin urmare

Din aceeași egalitate (deoarece $\overrightarrow(BC)$ și $\overrightarrow(AD)$ sunt codirecționale și, prin urmare, coliniare) obținem acel $MN||AD$.

Teorema a fost demonstrată.

Exemple de probleme privind conceptul de linie mediană a unui trapez

Exemplul 1

Laturile laterale ale trapezului sunt $15\ cm$ și, respectiv, $17\ cm$. Perimetrul trapezului este $52\cm$. Aflați lungimea liniei mediane a trapezului.

Soluţie.

Să notăm linia mediană a trapezului cu $n$.

Suma laturilor este egală cu

Prin urmare, deoarece perimetrul este $52\ cm$, suma bazelor este egală cu

Deci, prin teorema 1, obținem

Răspuns:$10\cm$.

Exemplul 2

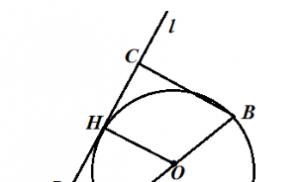
Capetele diametrului cercului sunt de $9$ cm și, respectiv, $5$ cm distanță de tangenta acestuia.Aflați diametrul acestui cerc.

Soluţie.

Să ni se dă un cerc cu centrul în punctul $O$ și diametrul $AB$. Să desenăm o tangentă $l$ și să construim distanțele $AD=9\ cm$ și $BC=5\ cm$. Să desenăm raza $OH$ (Fig. 2).

Figura 2.

Deoarece $AD$ și $BC$ sunt distanțe până la tangentă, atunci $AD\bot l$ și $BC\bot l$ și deoarece $OH$ este raza, atunci $OH\bot l$, prin urmare, $OH |\left|AD\right||BC$. Din toate acestea rezultă că $ABCD$ este un trapez, iar $OH$ este linia sa mediană. Prin teorema 1, obținem

Conceptul liniei mediane a trapezului

În primul rând, să ne amintim ce fel de figură se numește trapez.

Definiția 1

Un trapez este un patrulater în care două laturi sunt paralele, iar celelalte două nu sunt paralele.

În acest caz, laturile paralele se numesc bazele trapezului, iar laturile neparalele se numesc laturile laterale ale trapezului.

Definiția 2

Linia mediană a unui trapez este un segment care leagă punctele medii ale laturilor laterale ale trapezului.

Teorema liniei mediane a trapezului

Acum introducem teorema despre linia mediană a unui trapez și o demonstrăm folosind metoda vectorială.

Teorema 1

Linia mediană a trapezului este paralelă cu bazele și egală cu jumătatea sumei acestora.

Dovada.

Să ni se dea un trapez $ABCD$ cu bazele $AD\ și\ BC$. Și să fie $MN$ linia de mijloc a acestui trapez (Fig. 1).

Figura 1. Linia mediană a trapezului

Să demonstrăm că $MN||AD\ și\ MN=\frac(AD+BC)(2)$.

Luați în considerare vectorul $\overrightarrow(MN)$. Apoi folosim regula poligonului pentru a adăuga vectori. Pe de o parte, înțelegem asta

Pe cealaltă parte

Să adunăm ultimele două egalități și să obținem

Deoarece $M$ și $N$ sunt punctele medii ale laturilor laterale ale trapezului, vom avea

Primim:

Prin urmare

Din aceeași egalitate (deoarece $\overrightarrow(BC)$ și $\overrightarrow(AD)$ sunt codirecționale și, prin urmare, coliniare) obținem acel $MN||AD$.

Teorema a fost demonstrată.

Exemple de probleme privind conceptul de linie mediană a unui trapez

Exemplul 1

Laturile laterale ale trapezului sunt $15\ cm$ și, respectiv, $17\ cm$. Perimetrul trapezului este $52\cm$. Aflați lungimea liniei mediane a trapezului.

Soluţie.

Să notăm linia mediană a trapezului cu $n$.

Suma laturilor este egală cu

Prin urmare, deoarece perimetrul este $52\ cm$, suma bazelor este egală cu

Deci, prin teorema 1, obținem

Răspuns:$10\cm$.

Exemplul 2

Capetele diametrului cercului sunt de $9$ cm și, respectiv, $5$ cm distanță de tangenta acestuia.Aflați diametrul acestui cerc.

Soluţie.

Să ni se dă un cerc cu centrul în punctul $O$ și diametrul $AB$. Să desenăm o tangentă $l$ și să construim distanțele $AD=9\ cm$ și $BC=5\ cm$. Să desenăm raza $OH$ (Fig. 2).

Figura 2.

linia de mijloc figuri în planimetrie - un segment care leagă punctele mijlocii a două laturi ale unei figuri date. Conceptul este folosit pentru următoarele figuri: triunghi, patrulater, trapez.

Linia de mijloc a triunghiului

Proprietăți

linia de mijloc a triunghiului este paralelă cu baza și egală cu jumătate din aceasta.
linia de mijloc taie un triunghi similar și omotetic cu cel original cu un coeficient de 1/2; aria sa este egală cu un sfert din aria triunghiului original.
cele trei linii de mijloc împart triunghiul original în patru triunghiuri egale. Centrala acestor triunghiuri se numește triunghi complementar sau medial.

Semne

Dacă un segment dintr-un triunghi trece prin mijlocul uneia dintre laturile sale, o intersectează pe a doua și este paralel cu a treia, atunci acest segment este linia mediană.
Aria și, în consecință, volumul triunghiului tăiat de linia din mijloc este egală cu 1/4 din zonă și, în consecință, volumul întregului triunghi dat.

Linia mediană a unui patrulater

Linia mediană a unui patrulater- un segment care leagă punctele medii ale laturilor opuse ale unui patrulater.

Proprietăți

Prima linie leagă 2 laturi opuse. Al doilea leagă celelalte 2 părți opuse. Al treilea conectează centrele a două diagonale (nu în toate patrulaterele diagonalele sunt împărțite la jumătate în punctul de intersecție).

Dacă într-un patrulater convex linia de mijloc formează unghiuri egale cu diagonalele patrulaterului, atunci diagonalele sunt egale.
Lungimea liniei mediane a unui patrulater este mai mică de jumătate din suma celorlalte două laturi sau egală cu aceasta dacă aceste laturi sunt paralele și numai în acest caz.
Punctele de mijloc ale laturilor unui patrulater arbitrar sunt vârfurile unui paralelogram. Aria sa este egală cu jumătate din aria patrulaterului, iar centrul său se află în punctul de intersecție al liniilor de mijloc. Acest paralelogram se numește paralelogramul Varignon;
Ultimul punct înseamnă următoarele: Într-un patrulater convex poți desena patru linii mediane de al doilea fel. Linii mediane de al doilea fel- patru segmente în interiorul unui patrulater, care trec prin punctele medii ale laturilor sale adiacente paralele cu diagonalele. Patru linii mediane de al doilea fel a unui patrulater convex, tăiați-l în patru triunghiuri și un patrulater central. Acest patrulater central este un paralelogram Varignon.
Punctul de intersecție al liniilor mediane ale unui patrulater este punctul lor de mijloc comun și bisectează segmentul care leagă punctele de mijloc ale diagonalelor. În plus, este centroidul vârfurilor patrulaterului.
Într-un patrulater arbitrar, vectorul liniei de mijloc este egal cu jumătate din suma vectorilor bazelor.

Linia mediană a trapezului

Linia mediană a trapezului- un segment care leagă punctele medii ale laturilor acestui trapez. Segmentul care leagă punctele medii ale bazelor trapezului se numește a doua linie mediană a trapezului.

Se calculează folosind formula: E F = A D + B C 2 (\displaystyle EF=(\frac (AD+BC)(2))), Unde ANUNȚȘi B.C.- baza trapezului.

În acest articol vom încerca să reflectăm proprietățile unui trapez cât mai complet posibil. În special, vom vorbi despre caracteristicile și proprietățile generale ale unui trapez, precum și despre proprietățile unui trapez înscris și ale unui cerc înscris într-un trapez. Vom atinge, de asemenea, proprietățile unui trapez isoscel și dreptunghiular.

Un exemplu de rezolvare a unei probleme folosind proprietățile discutate vă va ajuta să o sortați în locuri din cap și să vă amintiți mai bine materialul.

Trapez și toate-toate-toate

Pentru început, să ne amintim pe scurt ce este un trapez și ce alte concepte sunt asociate cu acesta.

Deci, un trapez este o figură patrulateră, ale cărei două laturi sunt paralele între ele (acestea sunt bazele). Și cele două nu sunt paralele - acestea sunt părțile laterale.

Într-un trapez, înălțimea poate fi coborâtă - perpendicular pe baze. Linia centrală și diagonalele sunt desenate. De asemenea, este posibil să desenați o bisectoare din orice unghi al trapezului.

Vom vorbi acum despre diferitele proprietăți asociate cu toate aceste elemente și combinațiile lor.

Proprietățile diagonalelor trapezoidale

Pentru a fi mai clar, în timp ce citiți, schițați trapezul ACME pe o bucată de hârtie și desenați diagonalele în ea.

Dacă găsiți punctele medii ale fiecăreia dintre diagonale (să numim aceste puncte X și T) și le conectați, obțineți un segment. Una dintre proprietățile diagonalelor unui trapez este că segmentul HT se află pe linia mediană. Și lungimea sa poate fi obținută prin împărțirea diferenței bazelor la două: ХТ = (a – b)/2.
În fața noastră este același ACME trapez. Diagonalele se intersectează în punctul O. Să ne uităm la triunghiurile AOE și MOK, formate din segmente ale diagonalelor împreună cu bazele trapezului. Aceste triunghiuri sunt asemănătoare. Coeficientul de asemănare k al triunghiurilor se exprimă prin raportul bazelor trapezului: k = AE/KM.
Raportul ariilor triunghiurilor AOE și MOK este descris de coeficientul k 2 .
Același trapez, aceleași diagonale care se intersectează în punctul O. Numai de această dată vom lua în considerare triunghiurile pe care le-au format segmentele diagonalelor împreună cu laturile trapezului. Zonele triunghiurilor AKO și EMO au dimensiuni egale - ariile lor sunt aceleași.
O altă proprietate a unui trapez implică construcția diagonalelor. Deci, dacă continuați laturile AK și ME în direcția bazei mai mici, atunci mai devreme sau mai târziu se vor intersecta la un anumit punct. Apoi, trageți o linie dreaptă prin mijlocul bazelor trapezului. Intersectează bazele în punctele X și T.
Dacă extindem acum linia XT, atunci aceasta va lega împreună punctul de intersecție al diagonalelor trapezului O, punctul în care se intersectează prelungirile laturilor și mijlocul bazelor X și T.
Prin punctul de intersecție al diagonalelor vom trasa un segment care va conecta bazele trapezului (T se află pe baza mai mică KM, X pe AE mai mare). Punctul de intersecție al diagonalelor împarte acest segment în următorul raport: TO/OX = KM/AE.
Acum, prin punctul de intersecție al diagonalelor, vom trasa un segment paralel cu bazele trapezului (a și b). Punctul de intersecție îl va împărți în două părți egale. Puteți găsi lungimea segmentului folosind formula 2ab/(a + b).

Proprietățile liniei mediane a unui trapez

Desenați linia de mijloc în trapez paralel cu bazele sale.

Lungimea liniei mediane a unui trapez poate fi calculată adunând lungimile bazelor și împărțindu-le la jumătate: m = (a + b)/2.
Dacă desenați orice segment (înălțime, de exemplu) prin ambele baze ale trapezului, linia de mijloc îl va împărți în două părți egale.

Proprietatea Bisectoarei Trapezului

Selectați orice unghi al trapezului și trageți o bisectoare. Să luăm, de exemplu, unghiul KAE al ACME nostru trapez. După ce ați finalizat singur construcția, puteți verifica cu ușurință dacă bisectoarea taie de la bază (sau continuarea ei pe o linie dreaptă în afara figurii în sine) un segment de aceeași lungime ca și latura.

Proprietățile unghiurilor trapezoidale

Indiferent care dintre cele două perechi de unghiuri adiacente laturii pe care o alegeți, suma unghiurilor din pereche este întotdeauna 180 0: α + β = 180 0 și γ + δ = 180 0.
Să conectăm punctele medii ale bazelor trapezului cu un segment TX. Acum să ne uităm la unghiurile de la bazele trapezului. Dacă suma unghiurilor pentru oricare dintre ele este 90 0, lungimea segmentului TX poate fi calculată cu ușurință pe baza diferenței dintre lungimile bazelor, împărțită la jumătate: TX = (AE – KM)/2.
Dacă sunt trasate linii paralele prin laturile unui unghi trapez, acestea vor împărți laturile unghiului în segmente proporționale.

Proprietățile unui trapez isoscel (echilateral).

Într-un trapez isoscel, unghiurile de la orice bază sunt egale.
Acum construiți din nou un trapez pentru a vă face mai ușor să vă imaginați despre ce vorbim. Priviți cu atenție baza AE - vârful bazei opuse M este proiectat într-un anumit punct pe linia care conține AE. Distanța de la vârful A până la punctul de proiecție al vârfului M și linia de mijloc a unui trapez isoscel sunt egale.
Câteva cuvinte despre proprietatea diagonalelor unui trapez isoscel - lungimile lor sunt egale. Și, de asemenea, unghiurile de înclinare ale acestor diagonale față de baza trapezului sunt aceleași.
Numai în jurul unui trapez isoscel poate fi descris un cerc, deoarece suma unghiurilor opuse ale unui patrulater este 180 0 - o condiție prealabilă pentru aceasta.
Proprietatea unui trapez isoscel rezultă din paragraful anterior - dacă un cerc poate fi descris lângă trapez, acesta este isoscel.
Din caracteristicile unui trapez isoscel rezultă proprietatea înălțimii unui trapez: dacă diagonalele sale se intersectează în unghi drept, atunci lungimea înălțimii este egală cu jumătate din suma bazelor: h = (a + b)/2.
Din nou, trageți segmentul TX prin punctele medii ale bazelor trapezului - într-un trapez isoscel este perpendicular pe baze. Și, în același timp, TX este axa de simetrie a unui trapez isoscel.
De data aceasta, coborâți înălțimea de la vârful opus al trapezului pe baza mai mare (să-i spunem a). Veți obține două segmente. Lungimea uneia poate fi găsită dacă lungimile bazelor sunt adăugate și împărțite la jumătate: (a + b)/2. O obținem pe a doua când scădem pe cea mai mică din baza mai mare și împărțim diferența rezultată la două: (a – b)/2.

Proprietățile unui trapez înscris într-un cerc

Deoarece vorbim deja despre un trapez înscris într-un cerc, să ne oprim asupra acestei probleme mai detaliat. În special, acolo unde centrul cercului este în raport cu trapezul. Și aici este recomandat să vă faceți timp pentru a ridica un creion și a desena ceea ce va fi discutat mai jos. Astfel vei înțelege mai repede și vei aminti mai bine.

Locația centrului cercului este determinată de unghiul de înclinare al diagonalei trapezului față de latura sa. De exemplu, o diagonală se poate extinde din partea superioară a unui trapez în unghi drept pe lateral. În acest caz, baza mai mare intersectează centrul cercului circumscris exact în mijloc (R = ½AE).
Diagonala și latura se pot întâlni și la un unghi ascuțit - atunci centrul cercului se află în interiorul trapezului.
Centrul cercului circumscris poate fi în afara trapezului, dincolo de baza sa mai mare, dacă există un unghi obtuz între diagonala trapezului și latură.
Unghiul format de diagonala și baza mare a trapezului ACME (unghiul înscris) este jumătate din unghiul central care îi corespunde: MAE = ½MOE.
Pe scurt, despre două moduri de a găsi raza unui cerc circumscris. Metoda unu: uită-te cu atenție la desenul tău - ce vezi? Puteți observa cu ușurință că diagonala împarte trapezul în două triunghiuri. Raza poate fi găsită prin raportul dintre latura triunghiului și sinusul unghiului opus, înmulțit cu doi. De exemplu, R = AE/2*sinAME. Într-un mod similar, formula poate fi scrisă pentru oricare dintre laturile ambelor triunghiuri.
Metoda a doua: găsiți raza cercului circumscris prin aria triunghiului format din diagonala, latura și baza trapezului: R = AM*ME*AE/4*S AME.

Proprietățile unui trapez circumscris unui cerc

Puteți potrivi un cerc într-un trapez dacă este îndeplinită o condiție. Citiți mai multe despre el mai jos. Și împreună această combinație de cifre are o serie de proprietăți interesante.

Dacă un cerc este înscris într-un trapez, lungimea liniei sale mediane poate fi găsită cu ușurință adunând lungimile laturilor și împărțind suma rezultată la jumătate: m = (c + d)/2.
Pentru trapezul ACME, descris despre un cerc, suma lungimilor bazelor este egală cu suma lungimilor laturilor: AK + ME = KM + AE.
Din această proprietate a bazelor unui trapez, rezultă afirmația inversă: un cerc poate fi înscris într-un trapez a cărui sumă a bazelor este egală cu suma laturilor sale.
Punctul tangent al unui cerc cu raza r înscris într-un trapez împarte latura în două segmente, să le numim a și b. Raza unui cerc poate fi calculată folosind formula: r = √ab.
Și încă o proprietate. Pentru a evita confuzia, desenează și tu acest exemplu. Avem vechiul trapez ACME, descris în jurul unui cerc. Conține diagonale care se intersectează în punctul O. Triunghiurile AOK și EOM formate din segmentele diagonalelor și laturile laterale sunt dreptunghiulare.
Înălțimile acestor triunghiuri, coborâte la ipotenuze (adică laturile laterale ale trapezului), coincid cu razele cercului înscris. Și înălțimea trapezului coincide cu diametrul cercului înscris.

Proprietățile unui trapez dreptunghiular

Un trapez se numește dreptunghiular dacă unul dintre unghiurile sale este drept. Și proprietățile sale provin din această circumstanță.

Un trapez dreptunghiular are una dintre laturile sale perpendiculară pe bază.
Înălțimea și latura unui trapez adiacent unui unghi drept sunt egale. Acest lucru vă permite să calculați aria unui trapez dreptunghiular (formula generală S = (a + b) * h/2) nu numai prin înălțime, ci și prin latura adiacentă unghiului drept.
Pentru un trapez dreptunghiular, proprietățile generale ale diagonalelor unui trapez deja descrise mai sus sunt relevante.

Dovada unor proprietăți ale trapezului

Egalitatea unghiurilor la baza unui trapez isoscel:

Probabil ați ghicit deja că aici vom avea nevoie din nou de trapezul AKME - desenați un trapez isoscel. Desenați o linie dreaptă MT de la vârful M, paralelă cu latura lui AK (MT || AK).

Patrulaterul rezultat AKMT este un paralelogram (AK || MT, KM || AT). Deoarece ME = KA = MT, ∆ MTE este isoscel și MET = MTE.

AK || MT, deci MTE = KAE, MET = MTE = KAE.

Unde este AKM = 180 0 - MET = 180 0 - KAE = KME.

Q.E.D.

Acum, pe baza proprietății unui trapez isoscel (egalitatea diagonalelor), demonstrăm că ACME trapez este isoscel:

Mai întâi, să desenăm o linie dreaptă MX – MX || KE. Obținem un paralelogram KMHE (bază – MX || KE și KM || EX).

∆AMX este isoscel, deoarece AM = KE = MX și MAX = MEA.

MH || KE, KEA = MXE, deci MAE = MXE.

S-a dovedit că triunghiurile AKE și EMA sunt egale între ele, deoarece AM = KE și AE sunt latura comună a celor două triunghiuri. Și, de asemenea, MAE = MXE. Putem concluziona că AK = ME și de aici rezultă că trapezul AKME este isoscel.

Sarcina de revizuire

Bazele trapezului ACME sunt de 9 cm și 21 cm, latura laterală KA, egală cu 8 cm, formează un unghi de 150 0 cu baza mai mică. Trebuie să găsiți zona trapezului.

Rezolvare: De la vârful K coborâm înălțimea la baza mai mare a trapezului. Și să începem să ne uităm la unghiurile trapezului.

Unghiurile AEM și KAN sunt unilaterale. Aceasta înseamnă că în total dau 180 0. Prin urmare, KAN = 30 0 (pe baza proprietății unghiurilor trapezoidale).

Să luăm acum în considerare ∆ANC dreptunghiular (cred că acest punct este evident pentru cititori fără dovezi suplimentare). Din aceasta vom găsi înălțimea trapezului KH - într-un triunghi este un catet care se află opus unghiului de 30 0. Prin urmare, KH = ½AB = 4 cm.

Găsim aria trapezului folosind formula: S ACME = (KM + AE) * KN/2 = (9 + 21) * 4/2 = 60 cm 2.

Postfaţă

Dacă ați studiat cu atenție și atent acest articol, nu ați fost prea leneș să desenați trapeze pentru toate proprietățile date cu un creion în mâini și să le analizați în practică, ar fi trebuit să stăpâniți bine materialul.

Desigur, aici există o mulțime de informații, variate și uneori chiar confuze: nu este atât de greu să confundați proprietățile trapezului descris cu proprietățile celui înscris. Dar tu însuți ai văzut că diferența este uriașă.

Acum aveți o schiță detaliată a tuturor proprietăților generale ale unui trapez. Precum și proprietățile și caracteristicile specifice ale trapezelor isoscele și dreptunghiulare. Este foarte convenabil de utilizat pentru a se pregăti pentru teste și examene. Încearcă-l singur și distribuie link-ul prietenilor tăi!

site-ul web, atunci când copiați materialul integral sau parțial, este necesar un link către sursă.

YouTube enciclopedic

1 / 3

✪ Clasa a VIII-a, lecția 25, Linia de mijloc a unui triunghi

✪ geometrie LINIA DE MEDIU A UNUI TRIUNGHI Atanasyan clasa a VIII-a

✪ Linia de mijloc a triunghiului | Geometrie 7-9 clasa #62 | Lecție de informații

Subtitrări

Linia de mijloc a triunghiului

Proprietăți

linia de mijloc a triunghiului este paralelă cu baza și egală cu jumătate din aceasta.
când toate cele trei linii de mijloc se intersectează, se formează 4 triunghiuri egale, asemănătoare (chiar omotetice) cu cel inițial cu un coeficient de 1/2.
linia de mijloc taie un triunghi care este similar cu acesta, iar aria sa este egală cu un sfert din aria triunghiului original.
Cele trei linii de mijloc ale triunghiului îl împart în 4 triunghiuri egale (identice), similare cu triunghiul original. Toate cele 4 astfel de triunghiuri identice se numesc triunghiuri mediale. Cel central dintre aceste 4 triunghiuri identice se numește triunghi complementar.

Semne

dacă un segment este paralel cu una dintre laturile triunghiului și conectează punctul de mijloc al unei laturi a triunghiului de un punct situat pe cealaltă parte a triunghiului, atunci aceasta este linia mediană.

Linia mediană a unui patrulater

Linia mediană a unui patrulater- un segment care leagă punctele medii ale laturilor opuse ale unui patrulater.

Proprietăți

Dacă într-un patrulater convex linia de mijloc formează unghiuri egale cu diagonalele patrulaterului, atunci diagonalele sunt egale.
Lungimea liniei mediane a unui patrulater este mai mică de jumătate din suma celorlalte două laturi sau egală cu aceasta dacă aceste laturi sunt paralele și numai în acest caz.
Punctele de mijloc ale laturilor unui patrulater arbitrar sunt vârfurile unui paralelogram. Aria sa este egală cu jumătate din aria patrulaterului, iar centrul său se află în punctul de intersecție al liniilor de mijloc. Acest paralelogram se numește paralelogramul lui Varignon;
Ultimul punct înseamnă următoarele: Într-un patrulater convex poți desena patru linii mediane de al doilea fel. Linii mediane de al doilea fel- patru segmente în interiorul unui patrulater, care trec prin punctele medii ale laturilor sale adiacente paralele cu diagonalele. Patru linii mediane de al doilea fel a unui patrulater convex, tăiați-l în patru triunghiuri și un patrulater central. Acest patrulater central este un paralelogram Varignon.
Punctul de intersecție al liniilor mediane ale unui patrulater este punctul lor de mijloc comun și bisectează segmentul care leagă punctele de mijloc ale diagonalelor. Mai mult, ea este

Vizualizări