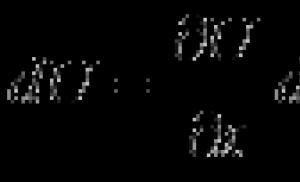Критическая сила сжатого стержня определяется по формуле. Формула Эйлера для определения критической силы сжатого стержня. Влияние способов закрепления концов стержня на величину критической силы. от способа закрепления стержня

В конструкциях и сооружениях большое применение находят детали, являющиеся относительно длинными и тонкими стержнями, у которых один или два размера поперечного сечения малы по сравнению с длиной стержня. Поведение таких стержней под действием осевой сжимающей нагрузки оказывается принципиально иным, чем при сжатии коротких стержней: при достижении сжимающей силой F некоторой критической величины, равной Fкр, прямолинейная форма равновесия длинного стержня оказывается неустойчивой, и при превышении Fкр стержень начинает интенсильно искривляется (выпучивается). При этом новым (моментным) равновесным состоянием упругого длинного становится некоторая новая уже криволинейная форма. Это явление носит название потери устойчивости.

Рис. 37. Потеря устойчивости

Устойчивость – способность тела сохранять положение или форму равновесия при внешних воздействиях.

Критическая сила (Fкр) – нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы (положения) тела. Условие устойчивости:

Fmax ≤ Fкр, (25)

Устойчивость сжатого стержня. Задача Эйлера .

При определении критической силы, вызывающей потерю устойчивости сжатого стержня, предполагается, что стержень идеально прямой и сила F приложена строго центрально. Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил Л. Эйлер в 1744 году.

Рис. 38. Сжатый стержень

Рассмотрим шарнирно опертый по концам стержень, сжатый продольной силой F. Положим, что по какой-то причине стержень получил малое искривление оси, вследствие чего в нем появился изгибающий момент M:

где y – прогиб стержня в произвольном сечении с координатой x.

Для определения критической силы можно воспользоваться приближенным дифференциальным уравнением упругой линии:

(26)

Проведя преобразования, можно увидеть, что минимальное значение критическая сила примет при n = 1 (на длине стержня укладывается одна полуволна синусоиды) и J = Jmin (стержень искривляется относительно оси с наименьшим моментом инерции)

(27)

Это выражение – формула Эйлера.

Зависимость критической силы от условий закрепления стержня.

Формула Эйлера была получена для, так называемого, основного случая – в предположении шарнирного опирания стержня по концам. На практике встречаются и другие случаи закрепления стержня. При этом можно получить формулу для определения критической силы для каждого из этих случаев, решая, как в предыдущем параграфе, дифференциальное уравнение изогнутой оси балки с соответствующими граничными условиями. Но можно использовать и более простой прием, если вспомнить, что, при потере устойчивости на длине стержня должна укладываться одна полуволна синусоиды.

Рассмотрим некоторые характерные случаи закрепления стержня по концам и получим общую формулу для различных видов закрепления.

Рис. 39. Различные случаи закрепления стержня

Общая формула Эйлера:

(28)

где μ·l = l пр – приведенная длина стержня; l – фактическая длина стержня; μ – коэффициент приведенной длины, показывающий во сколько раз необходимо изменить длину стержня, чтобы критическая сила для этого стержня стала равна критической силе для шарнирно опертой балки. (Другая интерпретация коэффициента приведенной длины: μ показывает, на какой части длины стержня для данного вида закрепления укладывается одна полуволна синусоиды при потере устойчивости.)

Таким образом, окончательно условие устойчивости примет вид

(29)

Рассмотрим два вида расчета на устойчивость сжатых стержней – проверочный и проектировочный.

Проверочный расчет

Порядок проверочного расчета на устойчивость выглядит так:

– исходя из известных размеров и формы поперечного сечения и условий закрепления стержня, вычисляем гибкость;

– по справочной таблице находим коэффициент понижения допускаемого напряжения, затем определяем допускаемое напряжение на устойчивость;

– сравниваем максимальное напряжение с допускаемым напряжением на устойчивость.

Проектировочный расчет

При проектировочном расчете (подобрать сечение под заданную нагрузку) в расчетной формуле имеются две неизвестные величины – искомая площадь поперечного сечения A и неизвестный коэффициент φ (так как φ зависит от гибкости стержня, а значит и от неизвестной площади A). Поэтому при подборе сечения обычно приходится пользоваться методом последовательных приближений.

Задача определения критической силы для сжатого стержня впервые была решена в 1744 году выдающимся математиком Леонардом Эйлером. Формула для критической силы была выведена Эйлером на примере идеального прямого стержня постоянного сечения, шарнирно закрепленного на концах (Рис.2).

Одна из опор стержня допускает возможность продольного перемещения соответствующего конца стержня. Собственный вес стержня не учитывалась. Искомая формула выглядела:

(2)

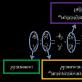
Формула Эйлера (2) для критической силы выводилась для стержня с шарнирным закрепления концов. Этот случай закрепления концов стержня принято называть основным случаем. В этом случае на длине стержня укладывается одна полуволна синусоиды. Однако, в практике встречаются различные другие случаи закрепления концов стержня. На рис.3 приведены некоторые из них, которые наиболее часто встречаются.

Для определения значения критической силы для каждого из приведенных случаев закрепления концов на практике применяется способ, который использует геометрическую аналогию между поведением упругой линии сжатого стержня с шарнирным закреплением концов (основной случай) и другим способом закрепления концов стержня. Согласно этим способом все остальные случаев закрепления концов стержня сводится к основному путем введения так называемой сводной или свободной длины стержня.
Сводной или свободной длиной стержня называется условная длина шарнирно закрепленного стержня, имеет такую ​​же критическую силу, как и стержень с заданным закреплением концов. Судить о сводную длину стержня можно по числу полуволн, которые укладываются на длине стержня. С геометрической аналогии следует, что в пределах сводной длины стержень с произвольным закреплением концов вести себя так же, как стержень с шарнирным закреплением концов.
Сводная длина стержня вычисляется следующим образом: , где длина стержня с заданным закреплением концов; коэффициент сводной длины.
Из определения сводной длины следует, что коэффициент есть такое число, на которое необходимо умножить длину стержня с заданным закреплением концов, чтобы получить такую ​​длину условного стержня с шарнирным закреплением концов, на котором заключается одна полуволна синусоиды.
Для стержня, изображенного на рис.3 , а длина условного стержня с шарнирным закреплением концов должно быть в два раза больше, чем заданная длина стержня. Верхняя часть условного стержня с шарнирным закреплением концов вести себя точно так же, как и стержень с заданным закреплением концов. Коэффициент возведения длины для этого случая равна. На рис.3 , в одна полуволна размещается на длине, составляющей 0,7 реальной длины стержня. Коэффициент возведения длины в этом случае составляет. Для случая жесткого закрепления обоих концов стержня (Рис.3 , г) длина полуволны, замеренная между двумя точками перегиба, составляет половину длины стержня. Для этого случая коэффициент. Для основного случая (Рис.3 , б) коэффициент, поскольку на его длине укладывается одна полуволна и, следовательно, сведена длина стержня равна реальной его длине.
Преобразуем формулу Эйлера (2) , подставляя в нее вместо реальной длины стержня сводную длину. Получаем формулу Эйлера для критической силы в окончательном виде:

(3)

На рис.3 приведены значения критической силы для стержней с различными условиями закрепления концов при одинаковых начальной длине и жесткости поперечного сечения. Следует отметить, что наибольшее значение критическая сила достигает для стержня с жестким закреплением концов (Рис.3 , г). В этом случае критическая сила оказывается в четыре раза больше, чем для основного случае закрепления концов. Наименее эффективным типом закрепления концов стержня является случай, приведенный на рис.3 , а. Критическая сила в этом случае оказывается в четыре раза меньше, чем для основного случая.

6.Структурный анализ плоского механизма. Формула Чебышева
Механизмом называется механическая система тел, в которой заданныедвижения одного или нескольких тел преобразуются в необходимое движениедругих тел. Таким образом, механизмы служат для преобразованиядвижения.
Механизмы часто являются составной частью машины (см. определение ма-шины в ) преобразуя движение ее двигателя
в необходимое движение рабочего органа.
Рассмотрим структуру механизма на примере
кривошипно-ползунного механизма (рис.1).
Механизм состоит из звеньев 1, 2, 3 и 4
которые представляют одну деталь или груп-
пу жестко соединенных деталей, имеющих
общий закон движения.
Звено 1 – ведущее звено, закон движе-
ния которого задан. Это звено также называют
входным звеном. Оно всегда обозначается со
стрелкой.
Звенья 2, 3 – ведомые звенья; звено 3 – называют также исполнительным
или выходным звеном. Оно совершает движение для получения, которого по-
лучен механизм.
Звено 4 – стойка или базовое звено, на котором устанавливаются осталь-
ные звенья. Движение всех звеньев в механизме рассматривается относительно
стойки.

Формула Эйлера : , где Е – модуль Юнга; – минимальный главный центральный момент инерции поперечного сечения стержня (очевидно, что при потере устойчивости изгиб стержня произойдет в плоскости наименьшей изгибной жесткости); – коэффициент приведения длины, зависящий от формы потери устойчивости; l – длина стержня. Произведение - приведенная длина стержня .

Формула Эйлера для шарнирно-опертого стержня, сжатого по концам

Для шарнирно опертого стержня, сжатого по концам, формула Эйлера для определения : (коэффициент приведения длины ).

Основной случай потери устойчивости – случай, когда при закреплении концов стержня и приложении нагрузки форма потери устойчивости представляет собой одну полуволну синусоиды (рис. 12.2, а).

Некоторые другие способы закрепления концов стержня (нагрузка по-прежнему приложена по торцам) легко могут быть приведены к основному случаю потери устойчивости путем сопоставления формы изогнутой оси с формой потери устойчивости шарнирно опертого стержня.

Формула Эйлера для стержня с защемленным и свободным концами

При потере устойчивости стержень с жестко защемленным одним и свободным другим концом изогнется, как показано на (рис. 12.2, б). Форма потери устойчивости этого стержня представляет собой четверть синусоиды. Приведенная длина равна (полуволна синусоиды имеет длину ), а эйлерова сила в четыре раза меньше, чем для основного случая. Формула Эйлера для стержня с защемленным и свободным концами: .

Формула Эйлера для стержня с защемленными концами

Для стержня, оба конца которого жестко защемлены, форма потери устойчивости такова, что одна полуволна синусоиды занимает половину длины стержня (рис. 12.2, в). Поэтому приведенная длина стержня равна (), а формула эйлеровой нагрузки .

Критической () принято называть истинную, а эйлеровой () – теоретическую нагрузку, при которой происходит потеря .

Формула Эйлера получена из предположения, что в момент потери устойчивости напряжения сжатия в стержне не превышают предела пропорциональности : . Модуль Юнга (Е) в формуле Эйлера свидетельствует о том, что вплоть до момента потери устойчивости выполнялся . Если потеря устойчивости происходит при напряжении меньшем, чем , то .

Для стержней, теряющих устойчивость при напряжении, превышающем предел пропорциональности (), использование формулы Эйлера принципиально неправильно и крайне опасно, поскольку критическая нагрузка (истинная нагрузка, при которой происходит потеря устойчивости) меньше эйлеровой нагрузки: .

Пределы применимости формулы Эйлера

Пределы применимости формулы Эйлера можно установить, предварительно введя понятие гибкости стержня. Определим эйлеровы напряжения , исходя из формулы Эйлера:

.

Рассмотрим стержень постоянного сечения, оба конца которого закреплены шарнирно (рис. 12.3). Стержень сжимается критической силой. Рассматриваем малые перемещения сечений стержня. Задавшись прогибом оси стержня в определенном сечении, найдем величину осевой сжимающей силы, при которой такой прогиб возможен. Будем считать, что напряжения в стержне не превышает предела пропорциональности.

Рис. 12.3. Схема изгиба стержня критической силой F кр .

Начало координат поместим в точке О , ось z направлена вдоль оси стержня, ось y – влево от начала координат. Определим прогиб стержня в произвольном сечении z .

Воспользуемся приближенным дифференциальным уравнением изогнутой оси стержня:

Определим изгибающий момент в произвольном сечении стержня:

Последнее выражение представляет собой однородное дифференциальное уравнение с постоянными коэффициентами.

Решение этого уравнения можно записать в виде гармонической функции:

у = A sinkz +B coskz .

Постоянные интегрирования А и В находятся из граничных условий:

при z = 0, у = 0, В = 0 и дифференциальное уравнение принимает следующий вид:

y = A sinkz .

Стержень изгибается по синусоиде.

При z = l, у = 0 A sinkl = 0.

Известно, что произведение двух сомножителей равно нулю, лишь в том случае, если один из сомножителей равен нулю. Разберем оба случая.

Пусть А = 0, то у(z) всегда равен нулю и прогиба вообще не существует. Это решение противоречит принятому предположению о том, что стержень прогнулся, т. е. А 0. Следовательно, должно выполняться условие sinkl = 0, откуда:

kl = 0, , 2 , 3 , …, n

где п – любое целое число.

Определим, какое значение п подходит к решению данной задачи. Рассмотрим условие

Из последнего выражения следует, что если k = 0, то F кр =0, т. е. стержень не нагружен, а это противоречит условию задачи. Следовательно, значение k = 0 можно исключить из решения. В общем случае имеем:

Приравняв F = F кр , получим выражение

где наименьшее значение сжимающей силы, при котором проис-

ходит продольный изгиб, поэтому следует принять п = 1.

Тогда уравнение для определения критической силы примет вид

Таким образом, стержень изгибается по синусоиде с одной полуволной.

При z = l /2 прогиб стержня имеет максимальное значение.

При n = 2 и n = 3 стержень изгибается по двум и трем полуволнам синусоиды соответственно (рис. 12.4, б, в).

Прогиб стержня в произвольном сечении под воздействием сжимающей силы можно определить по формуле

Потеря устойчивости стержня происходит в плоскостях наименьшей жесткости, т. е. J = J min , поэтому при определении критической силы следует учитывать наименьший осевой момент инерции сечения, тогда окончательно:

Таким образом, имеем формулу Эйлера (1744) для определения критической силы для стержня с двумя шарнирно закрепленными концами (основной случай).

Рис. 12.4. Схема изогнутой оси стержня при различных значениях n

Величина критической силы прямо пропорциональна наименьшей жесткости сечения и обратно пропорциональна квадрату длины стержня .

Как видно из формулы Эйлера, величина критической силы зависит от геометрических характеристик стержня и модуля упругости материала, но не зависит от прочностных характеристик материала.

Так, например, критическая сила F кр практически не зависит от марки стали.

Предельная растягивающая сила зависит от прочностных характеристик (в зависимости от марки стали она будет различной) и не зависит от длины стержня. Таким образом, можно утверждать, что имеется существенное различие между работой стержня на растяжение и сжатие.

Выше был рассмотрен так называемый основной случай закрепления концов сжатого стержня, когда оба конца стержня закреплены шарнирно. На практике применяются и другие способы закрепления концов стержня.

Рассмотрим, как влияют условия закрепления стержня на величину критической силы.

Второй случай : один конец стержня жестко защемлен, второй – свободен (рис. 12.5, а).

Рис. 12.5. Схема закрепления стержня по второму случаю

При потере устойчивости верхний конец стержня отклонится на некоторую величину и повернется, нижний защемленный конец останется вертикальным. Изогнутая ось получится такая же, как для одной половины стержня первого случая (рис. 12.5, б).

Для получения полного соответствия с первым случаем продолжим мысленно изогнутую ось стержня вниз. Тогда форма потери устойчивости будет полностью совпадать с первым случаем. Отсюда можно сделать вывод, что критическая сила для этого случая будет такая же, как и для пропорционально закрепленного по концам стержня длиной 2 м. Тогда

Третий случай: оба конца стержня жестко закреплены (рис. 12.6).

После потери устойчивости концы стержня не поворачиваются. Средняя часть стержня длиной l /2 вследствие симметрии будет работать в таких же условиях, что и стержень с шарнирно опертыми концами, но длиной l . Тогда, исходя из формулы, получим:

Рис. 12.6. Схема закрепления стержня

по третьему случаю

Четвертый случай: один конец стержня жестко защемлен, а другой – закреплен шарнирно. В этом случае верхняя часть стержня длиной приблизительно 2l /3 имеет вид полуволны синусоиды и находится в таких же условиях, что и стержень с шарнирными опорами на концах (рис. 12.7).

Рис. 12.7. Схема закрепления стержня

по четвертому случаю

Анализируя последние выражения для определения критической силы, приходим к выводу, что чем более жестко закреплены концы стержня, тем большую нагрузку данный стержень может воспринимать.

Поэтому зависимости для определения критической силы при различных условиях закрепления стержня можно объединить в одну формулу:

где приведенная длина стержня;

Коэффициент приведения длины стержня, зависящий от способа

закрепления концов стержня;

Фактическая длина стержня.

Понятие о приведенной длине стержня впервые было введено профессором Петербургского института путей сообщения Ф. С. Ясинским в 1892 году.

Необходимо также отметить, что при составлении формул для определения критических сил в стержнях с различными условиями закрепления по концам использовалась аналогия в формах потери устойчивости отдельных их участков.

Однако эти решения можно получить также строго математически. Для этого необходимо записать для каждого случая дифференциальное уравнение упругой линии стержня при потере устойчивости и решить его с использованием граничных условий.

Коэффициент продольной длины стержня в зависимости от условий его закрепления представлен на рис. 12.8.

Рис.12.8. Коэффициент приведения длины для различных случаев

закрепления концов стержня

Понятие об устойчивости и критической силе. Проектировочный и проверочный расчеты.

В конструкциях и сооружениях большое применение находят детали, являющиеся относительно длинными и тонкими стержнями, у которых один или два размера поперечного сечения малы по сравнению с длиной стержня. Поведение таких стержней под действием осевой сжимающей нагрузки оказывается принципиально иным, чем при сжатии коротких стержней: при достижении сжимающей силой F некоторой критической величины, равной Fкр, прямолинейная форма равновесия длинного стержня оказывается неустойчивой, и при превышении Fкр стержень начинает интенсильно искривляется (выпучивается). При этом новым (моментным) равновесным состоянием упругого длинного становится некоторая новая уже криволинейная форма. Это явление носит название потери устойчивости.

Рис. 37. Потеря устойчивости

Устойчивость - способность тела сохранять положение или форму равновесия при внешних воздействиях.

Критическая сила (Fкр) - нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы (положения) тела. Условие устойчивости:

Fmax ≤ Fкр, (25)

Устойчивость сжатого стержня. Задача Эйлера .

При определении критической силы, вызывающей потерю устойчивости сжатого стержня, предполагается, что стержень идеально прямой и сила F приложена строго центрально. Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил Л. Эйлер в 1744 году.

Рис. 38. Сжатый стержень

Рассмотрим шарнирно опертый по концам стержень, сжатый продольной силой F. Положим, что по какой-то причине стержень получил малое искривление оси, вследствие чего в нем появился изгибающий момент M:

где y - прогиб стержня в произвольном сечении с координатой x.

Для определения критической силы можно воспользоваться приближенным дифференциальным уравнением упругой линии:

(26)

Проведя преобразования, можно увидеть, что минимальное значение критическая сила примет при n = 1 (на длине стержня укладывается одна полуволна синусоиды) и J = Jmin (стержень искривляется относительно оси с наименьшим моментом инерции)

(27)

Это выражение - формула Эйлера.

Зависимость критической силы от условий закрепления стержня.

Формула Эйлера была получена для, так называемого, основного случая - в предположении шарнирного опирания стержня по концам. На практике встречаются и другие случаи закрепления стержня. При этом можно получить формулу для определения критической силы для каждого из этих случаев, решая, как в предыдущем параграфе, дифференциальное уравнение изогнутой оси балки с соответствующими граничными условиями. Но можно использовать и более простой прием, если вспомнить, что, при потере устойчивости на длине стержня должна укладываться одна полуволна синусоиды.

Рассмотрим некоторые характерные случаи закрепления стержня по концам и получим общую формулу для различных видов закрепления.

Рис. 39. Различные случаи закрепления стержня

Общая формула Эйлера:

(28)

где μ·l = l пр - приведенная длина стержня; l - фактическая длина стержня; μ - коэффициент приведенной длины, показывающий во сколько раз необходимо изменить длину стержня, чтобы критическая сила для этого стержня стала равна критической силе для шарнирно опертой балки. (Другая интерпретация коэффициента приведенной длины: μ показывает, на какой части длины стержня для данного вида закрепления укладывается одна полуволна синусоиды при потере устойчивости.)

Таким образом, окончательно условие устойчивости примет вид

(29)

Рассмотрим два вида расчета на устойчивость сжатых стержней - проверочный и проектировочный.

Проверочный расчет

Порядок проверочного расчета на устойчивость выглядит так:

Исходя из известных размеров и формы поперечного сечения и условий закрепления стержня, вычисляем гибкость;

По справочной таблице находим коэффициент понижения допускаемого напряжения, затем определяем допускаемое напряжение на устойчивость;

Сравниваем максимальное напряжение с допускаемым напряжением на устойчивость.

Проектировочный расчет

При проектировочном расчете (подобрать сечение под заданную нагрузку) в расчетной формуле имеются две неизвестные величины - искомая площадь поперечного сечения A и неизвестный коэффициент φ (так как φ зависит от гибкости стержня, а значит и от неизвестной площади A). Поэтому при подборе сечения обычно приходится пользоваться методом последовательных приближений:

Обычно в первой попытке принимают φ 1 = 0,5…0,6 и определяют площадь сечения в первом приближении

По найденной площади A1 подбирают сечение и вычисляют гибкость стержня в первом приближении λ1. Зная λ, находят новое значение φ′1;

Выбор материала и рациональной формы сечения.

Выбор материала . Так как в формулу Эйлера из всех механических характеристик входит лишь модуль Юнга, то для повышения устойчивости стержней большой гибкости нецелесообразно применять высокопрочные материалы, так как модуль Юнга для всех марок сталей примерно одинаков.

Для стержней малой гибкости применение высокосортных сталей оправдано, так как с повышением предела текучести у таких сталей повышаются и критические напряжения, а значит и запас устойчивости.