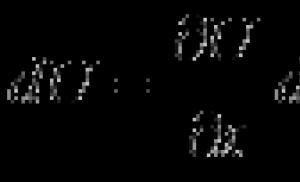Написать уравнение прямой l удовлетворяющей условию. Прямая линия. Уравнение прямой. уравнением прямой с угловым коэффициентом k

Если на плоскости введена ПДСК, то всякое уравнение первой степени относительно текущих координат и

, (5)

где иодновременно не равны нулю, определяет прямую.

Верно и обратное утверждение: в ПДСК любая прямая может быть задана уравнением первой степени вида (5).

Уравнение вида (5) называется общим уравнением прямой .

Частные случаи уравнения (5) приведены в следующей таблице.

	Значении коэффициентов	Уравнение прямой	Положение прямой
			Прямая проходит через начало координат
			Прямая параллельна оси
			Прямая параллельна оси
			Прямая совпадает с осью
			Прямая совпадает с осью

Уравнение прямой с угловым коэффициентом и начальной ординатой.

Углом наклона прямой к оси
называется наименьший угол
, на который нужно повернуть против часовой стрелки ось абсцисс до её совпадения с данной прямой (Рис.6). Направление любой прямой характеризуется еёугловым коэффициентом , который определяется как тангенс угла наклона
этой прямой, т. е.

.

Исключение составляет только прямая, перпендикулярная оси
, которая не имеет углового коэффициента.

Уравнение прямой, имеющей угловой коэффициент и пересекающей ось
в точке, ордината которой равна(начальная ордината) , записывается в виде

.

Уравнение прямой в отрезках

Уравнением прямой в отрезках называется уравнение вида

, (6)

где и
соответственно длины отрезков, отсекаемых прямой на координатных осях, взятые с определёнными знаками.

Уравнение прямой, проходящей через данную точку в данном направлении. Пучок прямых

Уравнение прямой, проходящей через данную точку
и имеющей угловой коэффициент записывается в виде

. (7)

Пучком прямых называется совокупность прямых плоскости, проходящих через одну и точку
центр пучка. Если известны координаты центра пучка, то уравнение (8) можно рассматривать как уравнение пучка, поскольку любая прямая пучка может быть получена из уравнения (8) при соответствующем значении углового коэффициента(исключение составляет прямая, которая параллельна оси
её уравнение
).

Если известны общие уравнения двух прямых, принадлежащих пучку
и(образующих пучка), то уравнении любой прямой из этого пучка можно записать в виде

Уравнение прямой, проходящей через две точки

Уравнение прямой, проходящей через две данные точки
и
, имеет вид

.

Если точки
и
определяют прямую, параллельную оси

или оси

, то уравнение такой прямой записывается соответственно в виде

или
.

Взаимное расположение двух прямых. Угол между прямыми. Условие параллельности. Условие перпендикулярности

Взаимное расположение двух прямых, заданных общими уравнениями

и ,

представлено в следующей таблице.

Под углом между двумя прямыми понимается один из смежных углов, образованных при их пересечении. Острый угол между прямыми
м
, определяется формулой

.

Заметим, что если хотя бы одна из данных прямых параллельна оси
, то формула (11) не имеет смысла, поэтому будем использовать общие уравнения прямых

и .

формула (11) примет вид

.

Условие параллельности:

или
.

Условие перпендикулярности:

или
.

Нормальное уравнение прямой. Расстояние точки от прямой. Уравнения биссектрис

Нормальное уравнение прямой имеет вид

где
длина перпендикуляра (нормали), опущенного из начала координат на прямую,
угол наклона этого перпендикуляра к оси
. Чтобы привести общее уравнение прямой
к нормальному виду, нужно обе части равенства (12) умножить нанормирующий множитель
, взятый со знаком противоположным знаку свободного члена.

Расстояние точки
от прямой найдём по формулам

. (9)

Уравнение биссектрис углов между прямыми
и :

.

Задача 16. Дана прямая
. Составить уравнение прямой, проходящей через точку
параллельно данной прямой.

Решение. По условию параллельности прямых
. Для решения задачи будем использовать уравнение прямой, проходящей через данную точку
в данном направлении (8):

.

Найдём угловой коэффициент данной прямой. Для этого от общего уравнения прямой (5) перейдём к уравнению с угловым коэффициентом (6) (выразим через):

Следовательно,
.

Задача 17 . Найти точку
, симметричную точке
, относительно прямой
.

Решение. Для того, чтобы найти точку симметричную точке относительно прямой(Рис.7) необходимо:

1) опустить из точки на прямуюперпендикуляр,

2) найти основание этого перпендикуляра
точку,

3) на продолжении перпендикуляра отложить отрезок
.

Итак, запишем уравнение прямой, проходящей через точку перпендикулярно данной прямой. Для этого воспользуемся уравнением прямой, проходящей через данную точку в данном направлении (8):

.

Подставим координаты точки
:

. (11)

Угловой коэффициент найдём из условия перпендикулярности прямых:

.

Угловой коэффициент данной прямой

,

следовательно, угловой коэффициент перпендикулярной прямой

.

Подставим его в уравнение (11):

Далее, найдём точку
точку пересечения данной прямой и ей перпендикулярной прямой. Так как точкапринадлежит обеим прямым, то её координаты удовлетворяют их уравнениям. Значит, для отыскания координат точки пересечения требуется решить систему уравнений, составленную из уравнений этих прямых:

Решение системы
,
, т. е.
.

Точка является серединой отрезка
, тогда из формул (4):

,
,

найдём координаты точки
:

Таким образом, искомая точка
.

Задача 18 .Составить уравнение прямой, которая проходит через точку
и отсекает от координатного угла треугольник с площадью, равной 150 кв.ед. (Рис.8).

Решение . Для решения задачи будем использовать уравнение прямой «в отрезках» (7):

. (12)

Так как точка
лежит на искомой прямой, то её координаты должны удовлетворять уравнению этой прямой:

.

Площадь треугольника, отсекаемого прямой от координатного угла вычисляется по формуле:

(записан модуль, так как имогут быть отрицательными).

Таким образом, получили систему для отыскания параметров и:

Эта система равносильна двум системам:

Решение первой системы
,
и
,
.

Решение второй системы
,
и
,
.

Подставим найденные значения в уравнение (12):

,
,
,
.

Запишем общие уравнения этих прямых:

,
,
,
.

Задача 19 . Вычислить расстояние между параллельными прямыми
и
.

Решение. Расстояние между параллельными прямыми равно расстоянию произвольной точки одной прямой до второй прямой.

Выберем на прямой точку
произвольно, следовательно, можно задать одну координату, т. е. например
, тогда
.

Теперь найдём расстояние точки до прямойпо формуле (10):

.

Таким образом, расстояние между данными параллельными прямыми равно.

Задача 20. Найти уравнение прямой, проходящей через точку пересечения прямых
и
(не находя точки пересечения) и

Решение . 1) Запишем уравнение пучка прямых с известными образующими (9):

Тогда искомая прямая имеет уравнение

Требуется найти такие значения
и, при которых прямая пучка пройдёт через точку
, т. е. её координаты должны удовлетворять уравнению (13):

Подставим найденное
в уравнение (13) и после упрощении получим искомую прямую:

.

.

Воспользуемся условием параллельности прямых:
. Найдём угловые коэффициенты прямыхи. Имеем, что
,
.

Следовательно,

Подставим найденное значение
в уравнение (13) и упростим, получим уравнение искомой прямой
.

Задачи для самостоятельного решения.

Задача 21. Составить уравнение прямой, проходящей через точки
и
: 1) с угловым коэффициентом; 2) общее; 3) «в отрезках».

Задача 22. Составить уравнение прямой, которая проходит через точку и образует с осью
угол
, если 1)
,
; 2)
,
.

Задача 23. Написать уравнения сторон ромба с диагоналями 10 см и 6 см, приняв большую диагональ за ось
, а меньшую
за ось
.

Задача 24. Равносторонний треугольник
со стороной, равной 2 единицам, расположен так, как показано на рисунке 9. составить уравнения его сторон.

Задача 25 . Через точку
провести прямую, отсекающую на положительных полуосях координат равные отрезки.

Задача 26 . Найти площадь треугольника, который отсекает от координатного угла прямая:

1)
; 2)
.

Задача 27 .Написать уравнение прямой, проходящей через точку и отсекающей от координатного угла треугольник площадью, равной, если

1)
,
кв. ед.; 2)
,
кв. ед.

Задача 28. Даны вершины треугольника
. Найти уравнение средней линии, параллельной стороне
, если

Мы говорили, что алгебраическая кривая второго порядка определяется алгебраическим уравнением второго степени относительно х и у . В общем виде такое уравнение записывается так

Ах 2 + Вху + Су 2 +Dx + Ey + F = 0, (6)

причем А 2 + В 2 + С 2 ¹ 0 (т.е. одновременно числа А, В, С в ноль не обращаются). Слагаемые Ах 2 , Вху , Су 2 называются старшими членами уравнения, число

называется дискриминантом этого уравнения. Уравнение (6) называется общим уравнением кривой второго порядка.

Для рассмотренных ранее кривых имеем:

Эллипс: Þ А = , В = 0, С = , D = Е = 0, F = –1,

окружность х 2 + у 2 = а 2 Þ А = С = 1, В = D = Е = 0, F = –а 2 , d = 1>0;

Гипербола: Þ А = , В = 0, С = – , D = Е = 0, F = –1,

d = – . < 0.

Парабола: у 2 = 2рх Þ А = В = 0, С=1, D = –2р , Е = F = 0, d = 0,

х 2 = 2ру Þ А = 1В = С= D = 0, Е = –2р , F = 0, d = 0.

Кривые, заданные уравнением (6), называются центральными кривыми, если d¹0. Если d> 0, то кривая эллиптического типа, если d<0, то кривая гиперболического типа. Кривые, для которых d = 0 являются кривыми параболического типа.

Доказано, что линия второго порядка в любой декартовой системе координат задается алгебраическим уравнением второго порядка. Только в одной системе уравнение имеет сложный вид (например, (6)), а в другой – более простой, например, (5). Поэтому удобно рассматривать такую систему координат, в которой изучаемая кривая записывается наиболее простым (например, каноническим) уравнением. Переход от одной системы координат, в которой кривая задается уравнением вида (6) к другой, где ее уравнение имеет более простой вид, называется преобразованием координат .

Рассмотрим основные виды преобразований координат.

I. Преобразование переноса координатных осей (с сохранением направления). Пусть в исходной системе координат ХОУ точка М имеет координаты (х , у х ¢, у ¢). Из чертежа видно, что координаты точки М в разных системах связаны соотношениями

(7), или (8).

Формулы (7) и (8) называются формулами преобразования координат.

II. Преобразование поворота координатных осей на угол a. Если в исходной системе координат ХОУ точка М имеет координаты (х , у ), а в новой системе координат ХО¢У она имеет координаты (х ¢, у ¢). То связь между этими координатами выражается формулами

, (9)

или

С помощью преобразования координат уравнение (6) можно привести к одному из следующих канонических уравнений.

1) – эллипс,

2) – гипербола,

3) у 2 = 2рх , х 2 = 2ру – парабола

4) а 2 х 2 – b 2 y 2 = 0 – пара пересекающихся прямых (рис. а)

5) y 2 – a 2 = 0 – пара параллельных прямых (рис. б)

6) x 2 –a 2 = 0 – пара параллельных прямых (рис. в)

7) y 2 = 0 – совпадающие прямые (ось ОХ)

8) x 2 = 0 – совпадающие прямые (ось ОУ)

9) а 2 х 2 + b 2 y 2 = 0 – точка (0, 0)

10) мнимый эллипс

11) y 2 + a 2 = 0– пара мнимых прямых

12) x 2 + a 2 = 0 пара мнимых прямых.

Каждое из этих уравнений является уравнением линии второго порядка. Линии, определяемые уравнениями 4 – 12, называют вырожденными кривыми второго порядка.

Рассмотрим примеры преобразования общего уравнения кривой к каноническому виду.

1) 9х 2 + 4у 2 – 54х + 8у + 49 = 0 Þ (9х 2 – 54х ) + (4у 2 + 8у ) + 49 = 0 Þ

9(х 2 – 6х + 9) + 4(у 2 + 2у + 1) – 81 – 4 + 49 = 0 Þ 9(х –3) 2 + 4(у + 1) = 36, Þ

.

Положим х ¢ = х – 3, у ¢ = у + 1, получим каноническое уравнение эллипса . Равенства х ¢ = х – 3, у ¢ = у + 1 определяют преобразование переноса системы координат в точку (3, –1). Построив старую и новую системы координат, нетрудно изобразить данный эллипс.

2) 3у 2 +4х – 12у +8 = 0. Преобразуем:

(3у 2 – 12у )+ 4 х +8 = 0

3(у 2 – 4у +4) ­– 12 + 4х +8 = 0

3(у – 2) 2 + 4(х –1) = 0

(у – 2) 2 = – (х – 1) .

Положим х ¢ = х – 1, у ¢ = у – 2, получим уравнение параболы у ¢ 2 = – х ¢. Выбранная замена соответствует переносу системы координат в точку О¢(1,2).

Как показано выше, уравнения одой и той же прямой можнозаписать по крайней мере в трех видах: общие уравнения прямой, параметрические уравнения прямой и канонические уравнения прямой. Рассмотрим вопрос о переходе от уравнений прямой одного вида к уравнениям прямой в другом виде.

Во-первых заметим, что если заданы уравнения прямой в параметрической форме, то тем самым заданы точка, через которую проходит прямая и направляющий вектор прямой. Поэтому не составляет труда записать уравнения прямой в канонической форме.

Пример .

Даны уравнения прямой в параметрической форме

Решение .

Прямая проходит через точку
и имеет направляющий вектор
. Следовательно, канонические уравнения прямой имеют вид

.

Аналогично решается задача о переходе от канонических уравнений прямой к параметрическим уравнениям прямой.

Переход от канонических уравнений прямой к общим уравнениям прямой рассматривается ниже на примере.

Пример .

Даны канонические уравнения прямой

.

Записать общие уравнения прямой.

Решение.

Запишем канонические уравнения прямой в виде системы двух уравнений

.

Избавляясь от знаменателей путем умножения обеих частей первого уравнения на 6, а второго уравнения на 4, получим систему

.

.

Полученная система уравнений и есть общие уравнения прямой.

Рассмотрим переход от общих уравнений прямой к параметрическим и каноническим уравнениям прямой. Чтобы записать канонические или параметрические уравнения прямой, надо знать точку, через которую проходит прямая, и направляющий вектор прямой. Если определить координаты двух точек
и
, лежащих на прямой, то в качестве направляющего вектора м можно взять вектор
. Координаты двух точек, лежащих на прямой, можно получить как решения системы уравнений, определяющих общие уравнения прямой. В качестве точки, через которую проходит прямая, можно взять любую из точек
и
. Проиллюстрируем сказанное выше на примере.

Пример .

Даны общие уравнения прямой

.

Решение .

Найдем координаты двух точек, лежащих на прямой, как решения этой системы уравнений. Полагая
, получим систему уравнений

.

Решая эту систему, находим
. Следовательно, точка
лежит на прямой. Полагая
, получаем систему уравнений

,

решая которую находим
. Следовательно, прямая проходит через точку
. Тогда в качестве направляющего вектора можно взять вектор

.

Итак, прямая проходит через точку
и имеет направляющий вектор
. Следовательно, параметрические уравнения прямой имеют вид

.

Тогда канонические уравнения прямой запишутся в виде

.

Другой способ нахождения направляющего вектора прямой по общим уравнениям прямой основан на том, что в этом случае заданы уравнения плоскостей, а значит и нормали к этим плоскостям.

Пусть общие уравнения прямой имеют вид

и- нормали к первой и второй плоскости, соответственно. Тогда вектор
можно взять в качестве направляющего вектора прямой. В самом деле, прямая, будучи линией пересечения этих плоскостей, одновременно перпендикулярна векторами. Следовательно, она коллинеарна вектору
и значит этот вектор можно взять в качестве направляющего вектора прямой. Рассмотрим пример.

Пример .

Даны общие уравнения прямой

.

Записать параметрические и канонические уравнения прямой.

Решение .

Прямая является линией пересечения плоскостей с нормалями
и
. Берем в качестве направляющего вектора прямой вектор

Найдем точку, лежащую на прямой. Найдем точку, лежащую на прямой. Пусть
. Тогда получаем систему

.

Решая систему, находим
.Следовательно, точка
лежит на прямой. Тогда параметрические уравнения прямой можно записать в виде

.

Канонические уравнения прямой имеют вид

.

Наконец, к каноническим уравнениям можно перейти исключив в одном из уравнений одну из переменных, а затем другую переменную. Рассмотрим этот метод на примере.

Пример .

Даны общие уравнения прямой

.

Записать канонические уравнения прямой.

Решение.

Исключим из второго уравнения переменную у, прибавив к нему первое, умноженное на четыре. Получим

.

.

Теперь исключим из второго уравнения переменную , прибавив к нему первое уравнение, умноженное на два. Получим

.

.

Отсюда получаем каноническое уравнение прямой

.

.

.

Свойства прямой в евклидовой геометрии.

Через любую точку можно провести бесконечно много прямых.

Через любые две несовпадающие точки можно провести единственную прямую.

Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются

параллельными (следует из предыдущего).

В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:

• прямые пересекаются;

• прямые параллельны;

• прямые скрещиваются.

Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия

задается на плоскости уравнением первой степени (линейное уравнение).

Общее уравнение прямой.

Определение . Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим

уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи:

. C = 0, А ≠0, В ≠ 0 - прямая проходит через начало координат

. А = 0, В ≠0, С ≠0 { By + C = 0} - прямая параллельна оси Ох

. В = 0, А ≠0, С ≠ 0 { Ax + C = 0} - прямая параллельна оси Оу

. В = С = 0, А ≠0 - прямая совпадает с осью Оу

. А = С = 0, В ≠0 - прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких - либо заданных

начальных условий.

Уравнение прямой по точке и вектору нормали.

Определение . В декартовой прямоугольной системе координат вектор с компонентами (А, В)

перпендикулярен прямой, заданной уравнением

Ах + Ву + С = 0.

Пример . Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).

Решение . Составим при А = 3 и В = -1 уравнение прямой: 3х - у + С = 0. Для нахождения коэффициента С

подставим в полученное выражение координаты заданной точки А. Получаем: 3 - 2 + C = 0, следовательно

С = -1. Итого: искомое уравнение: 3х - у - 1 = 0.

Уравнение прямой, проходящей через две точки.

Пусть в пространстве заданы две точки M 1 (x 1 , y 1 , z 1) и M2 (x 2, y 2 , z 2), тогда уравнение прямой ,

проходящей через эти точки:

Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На

плоскости записанное выше уравнение прямой упрощается:

если х 1 ≠ х 2 и х = х 1 , если х 1 = х 2 .

Дробь = k называется угловым коэффициентом прямой .

Пример . Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение . Применяя записанную выше формулу, получаем:

Уравнение прямой по точке и угловому коэффициенту.

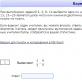
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и обозначить , то полученное уравнение называется

уравнением прямой с угловым коэффициентом k.

Уравнение прямой по точке и направляющему вектору.

По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание

прямой через точку и направляющий вектор прямой.

Определение . Каждый ненулевой вектор (α 1 , α 2) , компоненты которого удовлетворяют условию

Аα 1 + Вα 2 = 0 называется направляющим вектором прямой.

Ах + Ву + С = 0.

Пример . Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Решение . Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,

коэффициенты должны удовлетворять условиям:

1 * A + (-1) * B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.

при х = 1, у = 2 получаем С/ A = -3 , т.е. искомое уравнение:

х + у - 3 = 0

Уравнение прямой в отрезках.

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на -С, получим:

или , где

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения

прямой с осью Ох, а b - координатой точки пересечения прямой с осью Оу.

Пример . Задано общее уравнение прямой х - у + 1 = 0. Найти уравнение этой прямой в отрезках.

С = 1, , а = -1, b = 1.

Нормальное уравнение прямой.

Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется

нормирующем множителем , то получим

xcosφ + ysinφ - p = 0 - нормальное уравнение прямой .

Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0.

р - длина перпендикуляра, опущенного из начала координат на прямую,

а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

Пример . Дано общее уравнение прямой 12х - 5у - 65 = 0 . Требуется написать различные типы уравнений

этой прямой.

Уравнение этой прямой в отрезках :

Уравнение этой прямой с угловым коэффициентом : (делим на 5)

Уравнение прямой :

cos φ = 12/13; sin φ= -5/13; p = 5.

Следует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые,

параллельные осям или проходящие через начало координат.

Угол между прямыми на плоскости.

Определение . Если заданы две прямые y = k 1 x + b 1 , y = k 2 x + b 2 , то острый угол между этими прямыми

будет определяться как

Две прямые параллельны, если k 1 = k 2 . Две прямые перпендикулярны,

если k 1 = -1/ k 2 .

Теорема .

Прямые Ах + Ву + С = 0 и А 1 х + В 1 у + С 1 = 0 параллельны, когда пропорциональны коэффициенты

А 1 = λА, В 1 = λВ . Если еще и С 1 = λС , то прямые совпадают. Координаты точки пересечения двух прямых

находятся как решение системы уравнений этих прямых.

Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой.

Определение . Прямая, проходящая через точку М 1 (х 1 , у 1) и перпендикулярная к прямой у = kx + b

представляется уравнением:

Расстояние от точки до прямой.

Теорема . Если задана точка М(х 0 , у 0), то расстояние до прямой Ах + Ву + С = 0 определяется как:

Доказательство . Пусть точка М 1 (х 1 , у 1) - основание перпендикуляра, опущенного из точки М на заданную

прямую. Тогда расстояние между точками М и М 1 :

(1)

Координаты x 1 и у 1 могут быть найдены как решение системы уравнений:

Второе уравнение системы - это уравнение прямой, проходящей через заданную точку М 0 перпендикулярно

заданной прямой. Если преобразовать первое уравнение системы к виду:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

Теорема доказана.