1 un cerc poate fi înscris în orice triunghi. Cercuri înscrise și circumscrise. Lecția: Cercuri înscrise și circumscrise

Și se referă la toate părțile sale.

YouTube enciclopedic

• 1 / 5

  Proprietățile cercului înscris:

  r = (− a + b + c) (a − b + c) (a + b − c) 4 (a + b + c) ; (\displaystyle r=(\sqrt (\frac ((-a+b+c)(a-b+c)(a+b-c)))(4(a+b+c))));) 1 r = 1 h a + 1 h b + 1 h c (\displaystyle (\frac (1)(r))=(\frac (1)(h_(a)))+(\frac (1)(h_(b) ))+(\frac (1)(h_(c))))

  Unde a , b , c (\displaystyle a,b,c)- laturile triunghiului, h a , h b , h c (\displaystyle h_(a),h_(b),h_(c))- înălțimi trasate pe laturile corespunzătoare;

  r = S p = (p - a) (p - b) (p - c) p (\displaystyle r=(\frac (S)(p))=(\sqrt (\frac ((p-a)(p-b)) (p-c))(p))))

  Unde S (\displaystyle S) este aria triunghiului și p (\displaystyle p)- semiperimetrul acestuia.

  • Dacă A B (\displaystyle AB)- baza unui triunghi isoscel, cercul tangent la laturile unghiului ∠ A C B (\displaystyle \angle ACB) la puncte A (\displaystyle A)Și B (\displaystyle B), trece prin centrul cercului înscris al triunghiului △ A B C (\displaystyle \triunghi ABC).
  • teorema lui Euler: R 2 - 2 R r = | O I | 2 (\displaystyle R^(2)-2Rr=|OI|^(2)), Unde R (\displaystyle R)- raza cercului circumscris triunghiului, r (\displaystyle r)- raza cercului înscris în el, O (\displaystyle O)- centrul cercului circumscris, I (\displaystyle I)- centrul cercului înscris.
  • Dacă o dreaptă care trece prin punctul I paralel cu latura AB intersectează laturile BC și CA în punctele A 1 și B 1, atunci A 1 B 1 = A 1 B + A B 1 (\displaystyle A_(1)B_(1)=A_(1)B+AB_(1)).
  • Dacă punctele de tangenţă sunt înscrise într-un triunghi T (\displaystyle T) Conectați cercurile cu segmente, obțineți un triunghi T 1 cu următoarele proprietăți:
    • Bisectoarele lui T sunt bisectoarele perpendiculare ale lui T 1
    • Fie T 2 ortotriunghiul T 1 . Atunci laturile sale sunt paralele cu laturile triunghiului original T.
    • Fie T 3 punctul de mijloc al triunghiului T 1 . Atunci bisectoarele lui T sunt înălțimile lui T 3 .
    • Fie T 4 un ortotriunghi al lui T 3 , atunci bisectoarele lui T sunt bisectoarele lui T 4 .
  • Raza unui cerc înscris într-un triunghi dreptunghic cu catetele a, b și ipotenuza c este egală cu a + b - c 2 (\displaystyle (\frac (a+b-c)(2))).
  • Distanța de la vârful C al triunghiului până la punctul în care cercul atinge latura este egală cu d = a + b - c 2 = p - c (\displaystyle d=(\frac (a+b-c)(2))=p-c).
  • Distanța de la vârful C la centrul cercului înscris este l c = r sin ⁡ (γ 2) (\displaystyle l_(c)=(\frac (r)(\sin((\frac (\gamma)(2)))))), unde r este raza cercului înscris și γ este unghiul vârfului C.
  • Distanța de la vârful C până la centrul cercului înscris poate fi găsită și folosind formulele l c = (p - c) 2 + r 2 (\displaystyle l_(c)=(\sqrt ((p-c)^(2)+r^(2))))Și l c = a b - 4 R r (\displaystyle l_(c)=(\sqrt (ab-4Rr)))
  • Teorema tridentului sau teorema trefoilului: Dacă D- punctul de intersecție al bisectoarei unghiului A cu cercul circumferitor al unui triunghi ABC, euȘi J- respectiv, centrele inscrisului si excercului tangente la latura B.C., Apoi | D I | = | D B | = | D C | = | D J | (\displaystyle |DI|=|DB|=|DC|=|DJ|).
  • Lema lui Verriera: lasă cercul V (\displaystyle V) priveste partile A B (\displaystyle AB), A C (\displaystyle AC)și arcuri B C (\displaystyle BC) cerc circumferitor al unui triunghi. Apoi punctele de tangență ale cercului V (\displaystyle V) cu laturile și centrul cercului înscris al unui triunghi A B C (\displaystyle ABC) stați pe aceeași linie dreaptă.
  • teorema lui Feuerbach. Cercul de nouă puncte le atinge pe toate trei excercuri, și cerc înscris. Punct de atingere Cercul lui EulerȘi cerc înscris cunoscut sub numele de punctul Feuerbach.

  Relația dintre un cerc înscris și un cerc circumscripțional

  R R = 4 S 2 p a b c = cos ⁡ α + cos ⁡ β + cos ⁡ γ − 1 ; (\displaystyle (\frac (r)(R))=(\frac (4S^(2))(pabc))=\cos \alpha +\cos \beta +\cos \gamma -1;)

  Definiția 2

  Un poligon care satisface condiția definiției 1 se numește circumscris unui cerc.

  Figura 1. Cerc înscris

  Teorema 1 (despre un cerc înscris într-un triunghi)

  Teorema 1

  Puteți înscrie un cerc în orice triunghi și doar unul.

  Dovada.

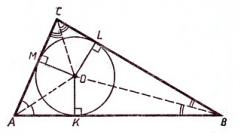
  Luați în considerare triunghiul $ABC$. Să desenăm bisectoare în el care se intersectează în punctul $O$ și să tragem perpendiculare din el pe laturile triunghiului (Fig. 2)

  

  Figura 2. Ilustrarea teoremei 1

  Existență: Să desenăm un cerc cu centrul în punctul $O$ și raza $OK.\ $Deoarece punctul $O$ se află pe trei bisectoare, este echidistant de laturile triunghiului $ABC$. Adică $OM=OK=OL$. În consecință, cercul construit trece și prin punctele $M\ și\ L$. Deoarece $OM,OK\ și\ OL$ sunt perpendiculare pe laturile triunghiului, atunci după teorema tangentei cercului, cercul construit atinge toate cele trei laturi ale triunghiului. Prin urmare, din cauza arbitrarului unui triunghi, un cerc poate fi înscris în orice triunghi.

  Unicitate: Să presupunem că un alt cerc cu centrul în punctul $O"$ poate fi înscris în triunghiul $ABC$. Centrul său este echidistant de laturile triunghiului și, prin urmare, coincide cu punctul $O$ și are o rază egală cu lungime $OK$ Dar atunci acest cerc va coincide cu primul.

  Teorema a fost demonstrată.

  Corolarul 1: Centrul unui cerc înscris într-un triunghi se află în punctul de intersecție al bisectoarelor sale.

  Iată câteva fapte legate de conceptul de cerc înscris:

  Nu orice patrulater poate încadra într-un cerc.

  În orice patrulater circumscris, sumele laturilor opuse sunt egale.

  Dacă sumele laturilor opuse ale unui patrulater convex sunt egale, atunci poate fi înscris un cerc în el.

  Definiția 3

  Dacă toate vârfurile unui poligon se află pe un cerc, atunci cercul se numește circumscris poligonului (Fig. 3).

  Definiția 4

  Un poligon care satisface definiția 2 se spune că este înscris într-un cerc.

  

  Figura 3. Cerc circumscris

  Teorema 2 (despre cercul circumferitor al unui triunghi)

  Teorema 2

  În jurul oricărui triunghi poți descrie un cerc și doar unul.

  Dovada.

  Luați în considerare triunghiul $ABC$. Să desenăm bisectoare perpendiculare în el, care se intersectează în punctul $O$ și să o conectăm cu vârfurile triunghiului (Fig. 4)

  

  Figura 4. Ilustrarea teoremei 2

  Existență: Să construim un cerc cu centrul în punctul $O$ și raza $OC$. Punctul $O$ este echidistant de vârfurile triunghiului, adică $OA=OB=OC$. În consecință, cercul construit trece prin toate vârfurile unui triunghi dat, ceea ce înseamnă că este circumscris acestui triunghi.

  Unicitate: Să presupunem că un alt cerc poate fi descris în jurul triunghiului $ABC$ cu centrul său în punctul $O"$. Centrul său este echidistant de vârfurile triunghiului și, prin urmare, coincide cu punctul $O$ și are o rază egală cu lungimea $OC.$ Dar atunci acest cerc va coincide cu primul.

  Teorema a fost demonstrată.

  Corolarul 1: Centrul cercului circumscris triunghiului coincide cu punctul de intersecție al perpendicularelor sale bisectoriale.

  Iată câteva fapte legate de conceptul de cerc circumscripționar:

  Nu este întotdeauna posibil să descrii un cerc în jurul unui patrulater.

  În orice patrulater ciclic, suma unghiurilor opuse este $(180)^0$.

  Dacă suma unghiurilor opuse ale unui patrulater este $(180)^0$, atunci se poate trasa un cerc în jurul lui.

  Un exemplu de problemă privind conceptele de cercuri înscrise și circumscrise

  Exemplul 1

  Într-un triunghi isoscel, baza are 8 cm și latura este de 5 cm. Aflați raza cercului înscris.

  Soluţie.

  Luați în considerare triunghiul $ABC$. Prin corolarul 1, știm că centrul cercului se află la intersecția bisectoarelor. Să desenăm bisectoarele $AK$ și $BM$, care se intersectează în punctul $O$. Să desenăm o perpendiculară $OH$ de la punctul $O$ la latura $BC$. Să desenăm o poză:

  

  Figura 5.

  Deoarece triunghiul este isoscel, atunci $BM$ este atât mediana, cât și înălțimea. După teorema lui Pitagora $(BM)^2=(BC)^2-(MC)^2,\ BM=\sqrt((BC)^2-\frac((AC)^2)(4))=\ sqrt (25-16)=\sqrt(9)=$3. $OM=OH=r$ -- raza necesară a cercului înscris. Deoarece $MC$ și $CH$ sunt segmente de tangente care se intersectează, atunci după teorema tangentelor care se intersectează, avem $CH=MC=4\ cm$. Prin urmare, $BH=5-4=1\ cm$. $BO=3-r$. Din triunghiul $OHB$, conform teoremei lui Pitagora, obținem:

  \[((3-r))^2=r^2+1\] \ \ \

  Răspuns:$\frac(4)(3)$.

  În această lecție ne vom aminti elementele de bază pe care se bazează teoria cercurilor înscrise și circumscrise, vom aminti caracteristicile patrulaterelor circumscrise și înscrise. În plus, vom deriva formule pentru găsirea razelor cercului circumscris și înscris în diferite cazuri.

  Subiect: Cercul

  Lecția: Cercuri înscrise și circumscrise

  În primul rând, vorbim despre cercuri înscrise și circumscrise relativ la un triunghi. Suntem pregătiți pentru acest subiect deoarece am studiat proprietățile bisectoarelor și bisectoarelor perpendiculare ale unui triunghi.

  Un cerc poate fi înscris în orice triunghi (vezi Fig. 1).

  Orez. 1

  Dovada:

  Știm că toate bisectoarele unui triunghi se intersectează într-un punct - să fie în punctul O. Să desenăm bisectoarele AO, BO, CO. Punctul lor de intersecție O este echidistant de laturile triunghiului. Este echidistant de laturile unghiului - AC și AB, deoarece aparține bisectoarei acestui unghi. La fel, este echidistant de laturile unghiurilor și astfel de cele trei laturi ale triunghiului.

  Să lăsăm perpendicularele din punctul O către laturile triunghiului - OM către latura AC, OL către BC, OK către AB. Aceste perpendiculare vor fi distanțele de la punctul O la laturile triunghiului și sunt egale:

  .

  Să notăm r distanța de la punctul O la laturile triunghiului și să considerăm un cerc cu un centru în punctul O și cu raza r.

  Cercul atinge linia dreaptă AB, deoarece are un punct comun K cu el, iar raza OK trasată în acest punct este perpendiculară pe dreapta AB. În mod similar, cercul atinge liniile AC și BC. Astfel, cercul atinge toate acele laturi ale triunghiului, ceea ce înseamnă că este înscris în triunghi.

  Deci, cele trei bisectoare ale unui triunghi se intersectează într-un punct care este centrul cercului.

  Să luăm în considerare o altă teoremă, ea se referă la punctul de intersecție al bisectoarelor perpendiculare ale unui triunghi. Știm că se intersectează într-un punct, iar acest punct coincide cu centrul cercului circumscris triunghiului.

  Un cerc poate fi desenat în jurul oricărui triunghi.

  Deci, este dat un triunghi. Să desenăm bisectoarea p 1 la latura triunghiului BC, p 2 la latura AB, p 3 la latura AC (vezi Fig. 2).

  

  Conform teoremei privind proprietățile bisectoarelor perpendiculare, un punct aparținând bisectoarei perpendiculare a unui segment este echidistant de capetele segmentului. Prin urmare, pentru că punctul Q aparține bisectoarei perpendiculare pe segmentul AC. De asemenea. Astfel, punctul Q este echidistant de vârfurile triunghiului. Prin urmare, QA, QB, QC sunt raze

  

  Orez. 2

  cerc circumscris unui triunghi. Să notăm raza ca R. Punctul O al intersecției bisectoarelor este centrul cercului circumscris.

  Să considerăm un cerc înscris într-un anumit patrulater și proprietățile acestui patrulater (vezi Fig. 3).

  Să ne amintim proprietățile unui punct situat pe bisectoarea unui unghi.

  Este dat un unghi, bisectoarea sa este AL, punctul M se află pe bisectoare.

  Dacă punctul M se află pe bisectoarea unui unghi, atunci este echidistant de laturile unghiului, adică distanțele de la punctul M la AC și la BC ale laturilor unghiului sunt egale.

  

  Orez. 3

  Distanța de la un punct la o dreaptă este lungimea perpendicularei. Din punctul M trasăm perpendicularele MK pe latura AB și MR pe latura AC.

  Luați în considerare triunghiuri și . Acestea sunt triunghiuri dreptunghiulare și sunt egale pentru că... au o ipotenuză comună AM, iar unghiurile sunt egale, deoarece AL este bisectoarea unghiului. Astfel, triunghiurile dreptunghiulare sunt egale în ipotenuză și unghi ascuțit, rezultă că , care este ceea ce trebuia demonstrat. Astfel, un punct de pe bisectoarea unui unghi este echidistant de laturile acelui unghi.

  În plus, picioarele. Astfel, segmentele tangente trasate la un cerc dintr-un punct sunt egale.

  Deci, să revenim la patrulater. Primul pas este să desenați bisectoare în el.

  Toate bisectoarele unui patrulater se intersectează într-un punct - punctul O, centrul cercului înscris.

  Din punctul O coborâm perpendiculare pe laturile patrulaterului la punctele K, L, M, N și determinăm punctele de tangență (vezi Fig. 3).

  Tangentele trasate la un cerc dintr-un punct sunt egale între ele, astfel încât din fiecare vârf iese o pereche de tangente egale: , , , .

  

  Orez. 3

  Dacă un cerc poate fi înscris într-un patrulater, atunci sumele laturilor sale opuse sunt egale. Este ușor de dovedit:

  Să extindem parantezele:

  Astfel, am demonstrat o teoremă simplă, dar importantă.

  Dacă un cerc poate fi înscris într-un patrulater, atunci sumele laturilor sale opuse sunt egale.

  Teorema inversă este adevărată.

  Dacă într-un patrulater sumele laturilor opuse sunt egale, atunci se poate înscrie în el un cerc.

  Să considerăm un cerc circumscris unui patrulater.

  Dat un cerc cu centrul O și un patrulater arbitrar ABCD. Să luăm în considerare proprietățile acestui patrulater. Toate cele patru bisectoare perpendiculare ale unui patrulater dat se intersectează într-un punct: acest punct este centrul cercului circumferitor.

  Demonstrarea că toate cele patru bisectoare perpendiculare se intersectează într-un punct ar fi plictisitor. Există un alt semn. Să luăm în considerare unghiul ےА, acesta este unghiul înscris al unui cerc, se sprijină pe arc și este măsurat cu jumătate din gradul de măsură a acestui arc (vezi Fig. 4). Să notăm unghiul ےА ca , apoi arcul . În mod similar, desemnăm unghiul opus ےС ca , acesta este înscris în cerc și se sprijină pe arc . De aici arcul.

  

  Orez. 4

  Arcele formează un cerc complet. De aici:

  ,

  Împărțind expresia rezultată la doi, obținem:

  Deci, am demonstrat teorema directă.

  Teorema

  Dacă un cerc este circumscris în jurul unui patrulater, suma unghiurilor sale opuse este .

  Acesta este un semn necesar și suficient, adică teorema inversă este adevărată.

  Dacă suma unghiurilor opuse ale unui patrulater este , în jurul acestui patrulater poate fi trasat un cerc.

  Pe baza acestor teoreme, observăm că este imposibil să descriem un cerc în jurul unui paralelogram, deoarece unghiurile sale opuse sunt egale și suma lor nu este egală (vezi Fig. 5).

  

  Orez. 5

  Un cerc ar putea fi descris în jurul unui paralelogram dacă unghiurile sale opuse ar fi egale cu 90°, adică dacă ar fi un dreptunghi, astfel un cerc ar putea fi descris în jurul unui dreptunghi (vezi Fig. 6).

  

  Orez. 6

  De asemenea, este imposibil să descrii un cerc în jurul unui romb, dar acesta poate fi înscris, deoarece toate laturile unui romb sunt egale și, prin urmare, sumele laturilor opuse ale unui romb sunt egale.

  În plus, într-un romb, fiecare diagonală este o bisectoare, punctul de intersecție al bisectoarelor este echidistant de toate laturile rombului (vezi Fig. 7).

  

  Orez. 7

  Deci, am demonstrat că un cerc poate fi înscris în orice triunghi, iar centrul acestui cerc coincide cu punctul de intersecție al bisectoarelor triunghiului. De asemenea, am demonstrat că un cerc poate fi descris în jurul oricărui triunghi, iar centrul său va coincide cu punctul de intersecție al bisectoarelor perpendiculare. În plus, am văzut că unele patrulatere pot fi înscrise cu un cerc, iar pentru a face acest lucru este necesar ca sumele laturilor opuse ale patrulaterului să fie egale. Am mai arătat că în jurul unor patrulatere este posibil să se descrie un cerc, iar o condiție necesară și suficientă pentru aceasta este egalitatea sumei unghiurilor opuse.

  Bibliografie

  1. Alexandrov A.D. si altele.Geometrie, clasa a VIII-a. - M.: Educație, 2006.
  2. Butuzov V.F., Kadomtsev S.B., Prasolov V.V. Geometrie, clasa a VIII-a. - M.: Educație, 2011.
  3. Merzlyak A.G., Polonsky V.B., Yakir S.M. Geometrie, clasa a VIII-a. - M.: VENTANA-GRAF, 2009.
  1. Uztest.ru ().
  2. Mschool.kubsu.ru ().
  3. Ege-study.ru ().

  Teme pentru acasă

  Definiția 2

  Un poligon care satisface condiția definiției 1 se numește circumscris unui cerc.

  Figura 1. Cerc înscris

  Teorema 1 (despre un cerc înscris într-un triunghi)

  Teorema 1

  Puteți înscrie un cerc în orice triunghi și doar unul.

  Dovada.

  Luați în considerare triunghiul $ABC$. Să desenăm bisectoare în el care se intersectează în punctul $O$ și să tragem perpendiculare din el pe laturile triunghiului (Fig. 2)

  

  Figura 2. Ilustrarea teoremei 1

  Existență: Să desenăm un cerc cu centrul în punctul $O$ și raza $OK.\ $Deoarece punctul $O$ se află pe trei bisectoare, este echidistant de laturile triunghiului $ABC$. Adică $OM=OK=OL$. În consecință, cercul construit trece și prin punctele $M\ și\ L$. Deoarece $OM,OK\ și\ OL$ sunt perpendiculare pe laturile triunghiului, atunci după teorema tangentei cercului, cercul construit atinge toate cele trei laturi ale triunghiului. Prin urmare, din cauza arbitrarului unui triunghi, un cerc poate fi înscris în orice triunghi.

  Unicitate: Să presupunem că un alt cerc cu centrul în punctul $O"$ poate fi înscris în triunghiul $ABC$. Centrul său este echidistant de laturile triunghiului și, prin urmare, coincide cu punctul $O$ și are o rază egală cu lungime $OK$ Dar atunci acest cerc va coincide cu primul.

  Teorema a fost demonstrată.

  Corolarul 1: Centrul unui cerc înscris într-un triunghi se află în punctul de intersecție al bisectoarelor sale.

  Iată câteva fapte legate de conceptul de cerc înscris:

  Nu orice patrulater poate încadra într-un cerc.

  În orice patrulater circumscris, sumele laturilor opuse sunt egale.

  Dacă sumele laturilor opuse ale unui patrulater convex sunt egale, atunci poate fi înscris un cerc în el.

  Definiția 3

  Dacă toate vârfurile unui poligon se află pe un cerc, atunci cercul se numește circumscris poligonului (Fig. 3).

  Definiția 4

  Un poligon care satisface definiția 2 se spune că este înscris într-un cerc.

  

  Figura 3. Cerc circumscris

  Teorema 2 (despre cercul circumferitor al unui triunghi)

  Teorema 2

  În jurul oricărui triunghi poți descrie un cerc și doar unul.

  Dovada.

  Luați în considerare triunghiul $ABC$. Să desenăm bisectoare perpendiculare în el, care se intersectează în punctul $O$ și să o conectăm cu vârfurile triunghiului (Fig. 4)

  

  Figura 4. Ilustrarea teoremei 2

  Existență: Să construim un cerc cu centrul în punctul $O$ și raza $OC$. Punctul $O$ este echidistant de vârfurile triunghiului, adică $OA=OB=OC$. În consecință, cercul construit trece prin toate vârfurile unui triunghi dat, ceea ce înseamnă că este circumscris acestui triunghi.

  Unicitate: Să presupunem că un alt cerc poate fi descris în jurul triunghiului $ABC$ cu centrul său în punctul $O"$. Centrul său este echidistant de vârfurile triunghiului și, prin urmare, coincide cu punctul $O$ și are o rază egală cu lungimea $OC.$ Dar atunci acest cerc va coincide cu primul.

  Teorema a fost demonstrată.

  Corolarul 1: Centrul cercului circumscris triunghiului coincide cu punctul de intersecție al perpendicularelor sale bisectoriale.

  Iată câteva fapte legate de conceptul de cerc circumscripționar:

  Nu este întotdeauna posibil să descrii un cerc în jurul unui patrulater.

  În orice patrulater ciclic, suma unghiurilor opuse este $(180)^0$.

  Dacă suma unghiurilor opuse ale unui patrulater este $(180)^0$, atunci se poate trasa un cerc în jurul lui.

  Un exemplu de problemă privind conceptele de cercuri înscrise și circumscrise

  Exemplul 1

  Într-un triunghi isoscel, baza are 8 cm și latura este de 5 cm. Aflați raza cercului înscris.

  Soluţie.

  Luați în considerare triunghiul $ABC$. Prin corolarul 1, știm că centrul cercului se află la intersecția bisectoarelor. Să desenăm bisectoarele $AK$ și $BM$, care se intersectează în punctul $O$. Să desenăm o perpendiculară $OH$ de la punctul $O$ la latura $BC$. Să desenăm o poză:

  

  Figura 5.

  Deoarece triunghiul este isoscel, atunci $BM$ este atât mediana, cât și înălțimea. De teorema lui Pitagora$(BM)^2=(BC)^2-(MC)^2,\ BM=\sqrt((BC)^2-\frac((AC)^2)(4))=\sqrt(25- 16)=\sqrt(9)=3$. $OM=OH=r$ -- raza necesară a cercului înscris. Deoarece $MC$ și $CH$ sunt segmente de tangente care se intersectează, atunci după teorema tangentelor care se intersectează, avem $CH=MC=4\ cm$. Prin urmare, $BH=5-4=1\ cm$. $BO=3-r$. Din triunghiul $OHB$, conform teoremei lui Pitagora, obținem:

  \[((3-r))^2=r^2+1\] \ \ \

  Răspuns:$\frac(4)(3)$.