Orice forță provoacă mișcare de rotație. Dinamica mișcării de rotație a unui corp rigid (2) - Curs. Lucrul forței în timpul mișcării de rotație

Când se observă mișcări complexe, cum ar fi mișcarea corpului uman (mers, alergare, sărituri etc.), pare dificil sau chiar imposibil să descrii mișcarea tuturor punctelor sale. Totuși, analizând astfel de mișcări, se poate observa că ele constau în mișcări de translație și rotație mai simple.

Mecanica mișcării de translație este cunoscută cititorului, așa că secțiunea începe cu o analiză a mișcării de rotație. Cea mai simplă este rotirea unui corp rigid în jurul unei axe fixe. Acest caz vă permite să vă familiarizați cu specificul, terminologia și legile mișcării de rotație.

5.1. CINEMATICA MIȘCĂRII DE ROTAȚIE A UNUI CORPS ABSOLUT RIGID ÎN jurul unei axe fixe

Un corp absolut rigid este unul a cărui distanță între oricare două puncte este constantă.

Dimensiunile și forma unui corp absolut rigid nu se schimbă atunci când se mișcă.

Conceptul de „corp absolut rigid” este o abstractizare fizică, deoarece orice corp este capabil de deformare. Cu toate acestea, în multe cazuri deformarea poate fi neglijată.

Cel mai simplu caz de mișcare de rotație a unui corp absolut rigid este rotația în jurul unei axe fixe. Aceasta este o astfel de mișcare în care punctele corpului se mișcă de-a lungul unor cercuri, ale căror centre se află pe o linie dreaptă, numită axa de rotație.

Se știe că în unele cazuri, pentru a caracteriza mișcarea unui corp, nu este necesară indicarea mișcării tuturor punctelor sale; deci, de exemplu, în mișcarea de translație este suficient să indicați mișcarea oricărui punct al corpului.

În timpul mișcării de rotație în jurul axei, punctele corpului se mișcă pe traiectorii diferite, dar, în același timp, toate punctele și corpul însuși se rotesc prin același unghi. Pentru a caracteriza rotația

desenați într-un plan perpendicular pe axă, vectorul rază până la un anumit punct i(Fig. 5.1). Dependența de timp a unghiului α de rotație al razei-vector față de o direcție selectată OX este ecuația pentru mișcarea de rotație a unui corp rigid în jurul unei axe fixe:

Viteza de rotație a corpului este caracterizată de o viteză unghiulară egală cu prima derivată a unghiului de rotație al vectorului-rază în raport cu timpul:

Viteza unghiulară este un vector care este direcționat de-a lungul axei de rotație și este legată de direcția de rotație prin regula șurubului din dreapta (Fig. 5.2). Vectorul viteză unghiulară, spre deosebire de vectorii viteză și forță, alunecă: nu are un punct de aplicare specific și poate fi localizat oriunde pe axa de rotație. Astfel, specificarea vectorului ω indică poziția axei de rotație, direcția de rotație și modulul vitezei unghiulare.

Viteza de modificare a vitezei unghiulare este caracterizată printr-o accelerație unghiulară egală cu prima derivată a vitezei unghiulare în raport cu timpul:

sau sub formă vectorială:

Din (5.4) se poate observa că vectorul accelerație unghiulară coincide în direcție cu o modificare elementară suficient de mică a vectorului viteză unghiulară dω : la rotație accelerată, accelerația unghiulară este direcționată în același mod ca și viteza unghiulară, la rotație lentă, este opusă acesteia.

Deoarece deplasarea unghiulară a tuturor punctelor unui corp absolut rigid este aceeași, atunci, conform (5.2) și (5.3), toate punctele corpului au în același timp aceeași viteză unghiulară și aceeași accelerație unghiulară. Caracteristicile liniare - mișcarea, viteza, accelerația - sunt diferite pentru puncte diferite. Să indicăm în formă scalară relația, care poate fi derivată independent, dintre caracteristicile liniare și unghiulare pentru al-lea punct care se deplasează de-a lungul unui cerc cu o rază. ri:

Orez. 5.3

În concluzie, prezentăm formulele pentru cinematica mișcării de rotație a unui corp rigid în jurul unei axe fixe, obținute prin integrarea expresiilor corespunzătoare:

ecuația mișcării uniforme de rotație[cm. (5.2)]:

dependența vitezei unghiulare de timp în mișcarea uniformă de rotație[cm. (5.3)]:

ecuația mișcării uniforme de rotație[cm. (5.1) și (5.6)]:

Este util să comparăm aceste formule cu dependențe similare pentru mișcarea de translație.

5.2. NOȚIUNI DE BAZĂ. ECUAȚIA DINAMICEI MIȘCĂRII DE ROTAȚIE

Moment de putere _

Să la un moment dat i forță aplicată unui corp rigid F^, situat într-un plan perpendicular pe axa de rotație (fig. 5.4).

Momentul forței în jurul axei de rotație este produsul vectorial dintre vectorul rază a punctului i și forța:

Extindendu-l, puteți scrie:

Unde β - unghiul dintre vectori r iȘi F i . De la umărul puterii h i = r i sinβ (vezi Fig. 5.4), atunci

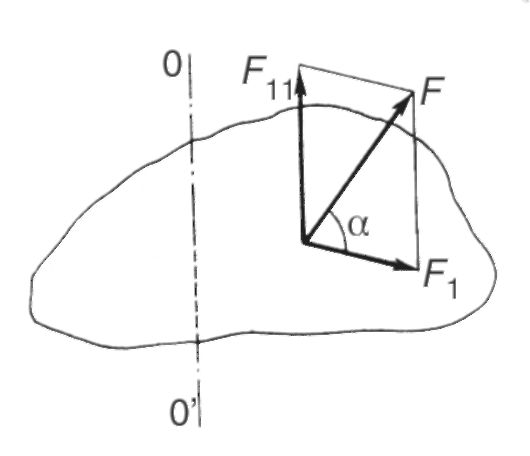
Dacă forța acționează la un anumit unghi α față de planul de rotație (Fig. 5.5), atunci ea poate fi descompusă în două componente. Unul dintre ele se află într-un plan perpendicular pe axa de rotație, iar celălalt este paralel cu această axă și nu afectează rotația corpului (în cazul real, afectează doar rulmenții). În cele ce urmează, vor fi luate în considerare doar forțele situate într-un plan perpendicular pe axa de rotație.

Orez. 5.4

Orez. 5.5

Lucrați în mișcare rotativă

Lăsați sub acțiunea forței F i(vezi Fig. 5.4) corpul se rotește printr-un unghi dα suficient de mic. Să găsim munca acestei forțe.

Expresia binecunoscută pentru munca de forță în acest caz ar trebui scrisă după cum urmează:

Asa de,

munca elementară a forței în mișcarea de rotație este egală cu produsul dintre momentul forței și unghiul elementar de rotație al corpului.

Dacă asupra corpului acționează mai multe forțe, atunci munca elementară efectuată de toate acestea este determinată în mod similar cu (5.12):

Unde M- momentul total al tuturor fortelor externe care actioneaza asupra corpului.

Dacă, atunci când corpul se rotește, poziția vectorului rază s-a schimbat de la α 1 la α 2, atunci munca forțelor externe poate fi găsită prin integrarea expresiei (5.13):

Moment de inerție

O măsură a inerției corpurilor aflate în mișcare de translație este masa. Inerția corpurilor în timpul mișcării de rotație depinde nu numai de masă, ci și de distribuția acesteia în spațiu față de axă. Măsura inerției corpului în timpul rotației este caracterizată de momentul de inerție al corpului în jurul axei de rotație. Să subliniem mai întâi că

momentul de inerție al unui punct material în jurul axei de rotație este o valoare egală cu produsul dintre masa punctului și pătratul distanței acestuia față de axă:

Momentul de inerție al unui corp în jurul unei axe este suma momentelor de inerție ale tuturor punctelor materiale care alcătuiesc corpul:

Ca exemplu, derivăm formula momentul de inerție al unei tije omogene subțiri lungime l si greutate Tîn jurul unei axe perpendiculare pe tijă și care trece prin mijlocul acesteia (fig. 5.6). Alegem o secțiune suficient de mică a tijei cu o lungime dx si greutate dm,îndepărtat de axa 00" la distanță X. Datorită micimii acestei zone, poate fi luată ca punct material, momentul său de inerție [vezi. (5.15)] este:

Masa unei secțiuni elementare este egală cu produsul densității liniare t/l,înmulțit cu lungimea secțiunii elementare: dm= (m/l) dx Inlocuind aceasta expresie in (5.18), obtinem

Pentru a afla momentul de inerție al întregii tije, integrăm expresia (5.19) peste întreaga tijă, i.e. între -1/2 și +1/2:

Să dăm expresii pentru momentele de inerție ale diferitelor corpuri simetrice cu masă T:

cilindru gol omogen(cerc) cu raza interioară rși externă R raportat la axa OO”, care coincide cu axa geometrică a cilindrului (Fig. 5.7):

continuu omogen cilindru (r = 0) sau disc [vezi (5.21)]:

minge uniformă despre axa care trece prin centrul ei:

cuboid în raport cu axa OO „trecând prin centrul său perpendicular pe planul bazei (Fig. 5.8):

În toate aceste exemple, axa de rotație trece prin centrul de masă al corpului. Când rezolvați probleme pentru a determina momentul de inerție al unui corp în jurul unei axe care nu trece prin centrul de masă, puteți utiliza teorema Huygens. Conform acestei teoreme, momentul de inerție al unui corp în jurul unei axe OO ":

unde J 0 este momentul de inerție în jurul unei axe paralele care trece prin centrul de masă al corpului OO"; T- masa corpului; d- distanta dintre doua axe paralele (Fig. 5.9). Unitatea momentului de inerție este kilogram metru pătrat(kg-m2).

impuls unghiular

impuls unghiular(moment de impuls)un punct material care se rotește în jurul unei axe se numește valoare egală cu produsul impulsului punctului aflat la distanța sa de axa de rotație:

Momentul unghiular al unui corp care se rotește în jurul unei axe este egal cu suma momentului unghiular al punctelor care alcătuiesc acest corp:

Deoarece viteza unghiulară a tuturor punctelor unui corp rigid este aceeași, scoateți ω din semnul sumei [vezi. (5.29)], obținem:

(/ - momentul de inerție al corpului față de axă), sau sub formă vectorială:

Deci, momentul unghiular este egal cu produsul dintre momentul de inerție al punctului și viteza unghiulară. De aici rezultă că direcțiile momentului unghiular și ale vectorilor viteză unghiulară coincid. Unitatea de măsură a momentului unghiular este kilogram metru pătrat pe secundă(kg? m2?s -1).

Formula (5.31) este utilă pentru a compara cu o formulă similară pentru impulsul în mișcarea de translație.

Energia cinetică a unui corp în rotație

Când un corp se rotește, energia sa cinetică este suma energiilor cinetice ale punctelor individuale ale corpului. Pentru un corp rigid:

Este util să comparați expresia (5.32) cu o expresie similară pentru mișcarea de translație.

Diferențiând (5.32), obținem o modificare elementară a energiei cinetice în mișcare de rotație:

Ecuația de bază a dinamicii mișcării de rotație

Fie ca un corp rigid asupra căruia acționează forțele externe se rotește printr-un unghi suficient de mic da. Să echivalăm munca elementară a tuturor forțelor externe în timpul unei astfel de rotații [vezi Fig. (5.13)] modificare elementară a energiei cinetice [vezi (5.33)]: M dα = Jω dω , de unde:

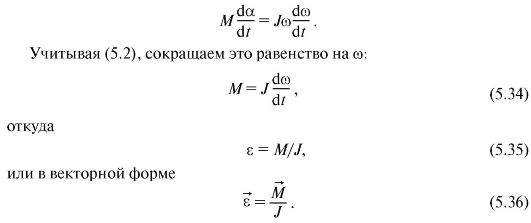
Asta e de bazăecuația dinamicii mișcării de rotație. Din (5.35) se poate observa că momentul de inerție caracterizează proprietățile inerțiale ale corpului în mișcare de rotație: sub acțiunea forțelor externe, accelerația unghiulară a corpului este cu atât mai mare, cu atât este mai mic momentul de inerție al corpului. .

Ecuația de bază pentru mișcarea de rotație joacă același rol ca a doua lege a lui Newton pentru translație. Mărimile fizice incluse în această ecuație sunt analoge cu forța, masa și respectiv accelerația.

Din (5.34) rezultă că:

Derivata momentului unghiular al corpului în raport cu timpul este egală cu momentul rezultant al tuturor forțelor externe.

Dependența accelerației unghiulare de momentul forței și momentul de inerție poate fi demonstrată folosind

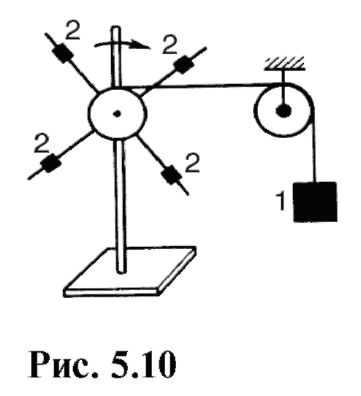
puterea dispozitivului prezentat în fig. 5.10. sub influența sarcinii 1, suspendată pe un fir aruncat peste un bloc, traversa se rotește rapid. Greutăți în mișcare 2 la diferite distanțe față de axa de rotație, puteți modifica momentul de inerție al crucii. Prin schimbarea sarcinilor, de ex. momentele de forță și momentul de inerție, se poate observa că accelerația unghiulară crește odată cu creșterea momentului de forță sau scăderea momentului de inerție.

5.3. LEGEA CONSERVĂRII CUPLULUI MOMENTULUI

Să luăm în considerare un caz special de mișcare de rotație, când momentul total al forțelor externe este egal cu zero. După cum se vede din (5.37), dl/dt= 0 la M = 0, de unde

Această poziție este cunoscută ca legea conservării momentului unghiular: dacă impulsul total al tuturor forțelor externe care acționează asupra unui corp este zero, atunci impulsul acestui corp rămâne constant.

Omițând demonstrația, observăm că legea conservării momentului unghiular este valabilă nu numai pentru un corp absolut rigid.

Cele mai interesante aplicații ale acestei legi sunt legate de rotația unui sistem de corpuri în jurul unei axe comune. În acest caz, este necesar să se țină cont de natura vectorială a momentului unghiular și a vitezelor unghiulare. Deci, pentru un sistem format din N corpuri care se rotesc în jurul unei axe comune, legea conservării momentului unghiular poate fi scrisă sub forma:

Să luăm în considerare câteva exemple care ilustrează această lege.

O gimnastă care efectuează sărituri (Fig. 5.11) în faza inițială își îndoaie genunchii și îi apasă pe piept, reducând astfel momentul de inerție și mărind viteza unghiulară de rotație în jurul unei axe orizontale care trece prin centrul de masă. La sfârșitul săriturii, corpul se îndreaptă, momentul de inerție crește, iar viteza unghiulară scade. Un patinator artistic care se rotește în jurul unei axe verticale (Fig. 5.12) la începutul rotației își aduce mâinile mai aproape de corp, reducând astfel momentul de inerție și mărind viteza unghiulară. La sfârșitul rotației, are loc procesul invers: când brațele sunt desfășurate, momentul de inerție crește și viteza unghiulară scade, ceea ce facilitează oprirea.

Același fenomen poate fi demonstrat și pe banca Jukovski, care este o platformă orizontală ușoară care se rotește cu frecare mică în jurul unei axe verticale. Când poziția mâinilor se schimbă, momentul de inerție și viteza unghiulară se modifică (Fig. 5.13), momentul unghiular rămâne constant. Pentru a spori efectul demonstrativ în mâinile unei persoane gantere. Pe banca lui Jukovski, se poate demonstra natura vectorială a legii conservării momentului unghiular.

Experimentatorul, stând pe o bancă fixă, primește de la asistent o roată de bicicletă care se rotește în jurul unei axe verticale (fig. 5.14, stânga). În acest caz, momentul impulsului sistemului om și platformei-roată este determinat doar de momentul impulsului roții:

aici J h - momentul de inerție al persoanei și al platformei; J K și ω κ - momentul de inerție și viteza unghiulară a roții. Deoarece momentul forțelor externe în jurul axei verticale este zero, atunci L se păstrează (L = const).

Dacă experimentatorul rotește axa de rotație a roții cu 180 ° (Fig. 5.14, din dreapta), atunci momentul unghiular al roții va fi direcționat opus celui original și egal cu J K ω K . Deoarece vectorul de impuls al roții se schimbă, iar momentul de impuls al sistemului este păstrat, atunci momentul de impuls al persoanei și al platformei trebuie să se schimbe inevitabil, acesta nu va mai fi egal cu zero 1 . Momentul unghiular al sistemului în acest caz

1 O ușoară discrepanță între axa roții și axa de rotație a platformei poate fi neglijată.

Folosind formula (5.42), se poate estima aproximativ momentul de inerție al corpului uman împreună cu platforma, pentru care este necesar să se măsoare ω κ , ω 4 și să se găsească J k . Metoda de măsurare a vitezelor unghiulare de rotație uniformă este cunoscută cititorului. Cunoscând masa roții și presupunând că masa este distribuită în principal de-a lungul jantei, J k poate fi determinat din formula (5.22). Pentru a reduce eroarea, puteți cântări janta unei roți de bicicletă punând pe ea anvelope speciale. Persoana trebuie să fie situată simetric față de axa de rotație.

O versiune mai simplă a demonstrației de mai sus constă în faptul că o persoană care stă pe banca lui Jukovski pune în rotație o roată pe care o ține pe o axă verticală. În acest caz, persoana și platforma încep să se rotească în direcții opuse (Fig. 5.15).

5.4. CONCEPTUL DE AXE LIBERE DE ROTARE

Un corp care se rotește în jurul unei axe fixe acționează în general asupra rulmenților sau a altor dispozitive care păstrează neschimbată poziția acelei axe. La viteze unghiulare mari și momente de inerție, aceste efecte pot fi semnificative. Cu toate acestea, în orice corp, puteți alege astfel de axe, a căror direcție în timpul rotației va fi păstrată fără dispozitive speciale. Pentru a înțelege ce condiție trebuie să îndeplinească alegerea unor astfel de axe, luați în considerare următorul exemplu.

Comparând (5.43) cu coordonatele centrului de masă, observăm că forțele care acționează asupra axei sunt echilibrate dacă axa de rotație trece prin centrul de masă.

Astfel, dacă axa de rotație trece perpendicular pe tijă prin centrul de masă, atunci nu va exista niciun impact asupra acestei axe din partea laterală a corpului rotativ. Dacă în același timp rulmenții sunt îndepărtați, atunci axa de rotație va începe să se miște, păstrându-și poziția în spațiu neschimbată, iar corpul va continua să se rotească în jurul acestei axe.

Axele de rotație, care, fără fixare specială, își păstrează direcția în spațiu, se numesc libere. Exemple de astfel de axe sunt axele de rotație ale Pământului și vârful de rotire, axa oricărui corp aruncat și care se rotește liber etc.

Un corp de formă arbitrară are întotdeauna cel puțin trei axe reciproc perpendiculare care trec prin centrul de masă, care pot fi axe de rotație libere. Aceste axe sunt numite axe principale de inerție. Deși toate cele trei axe principale de inerție sunt libere, rotația în jurul axei cu cel mai mare moment de inerție va fi cea mai stabilă. Faptul este că, ca urmare a acțiunii inevitabile a forțelor externe, cum ar fi frecarea, și, de asemenea, datorită faptului că este dificil să se stabilească rotația exact în jurul unei anumite axe, rotația în jurul axelor libere rămase este instabilă.

În unele cazuri, atunci când un corp se rotește în jurul unei axe libere cu un mic moment de inerție, el însuși schimbă această axă în axa cu cel mai mare moment.

Acest fenomen este demonstrat de următorul experiment. O tijă cilindrică este suspendată de motorul electric pe un filet, care se poate roti în jurul axei sale geometrice (Fig. 5.17, a). Moment de inerție față de această axă J 1 \u003d tR 2 / 2. Cu o viteză unghiulară suficient de mare, bastonul își va schimba poziția (Fig. 5.17, b). Momentul de inerție față de noua axă este J2 = ml 2/12. Dacă l 2 >6R 2 , atunci J 2 > J 1 . Rotația în jurul noii axe va fi stabilă.

Cititorul poate verifica independent din experiență că rotația unei cutii de chibrituri aruncate este stabilă în raport cu o axă care trece perpendicular pe fața mai mare și instabilă sau mai puțin stabilă în raport cu axele care trec perpendicular pe alte fețe (vezi Fig. 5.8).

Rotația animalelor și a oamenilor în zborul liber și în timpul diferitelor sărituri are loc în jurul axelor libere cu cel mai mare sau cel mai mic moment de inerție. Deoarece poziția centrului de masă depinde de postura corpului, vor exista diferite axe libere pentru diferite posturi.

5.5. CONCEPTUL DE GRADE DE LIBERTATE

Poziția unui punct material liber în spațiu este dată de trei coordonate independente: x, y, z. Dacă punctul nu este liber, dar se mișcă, de exemplu, de-a lungul unei suprafețe, atunci nu toate cele trei coordonate vor fi independente.

Variabilele independente care caracterizează poziția unui sistem mecanic se numesc grade de libertate.

Un punct material liber are trei grade de libertate, în exemplul considerat - două grade de libertate. Deoarece molecula unui gaz monoatomic poate fi considerată un punct material, prin urmare, o astfel de moleculă liberă are și trei grade de libertate.

Mai multe exemple.

Două puncte de material 1 și 2 sunt conectate rigid între ele. Poziția ambelor puncte este dată de șase coordonate x 1 , y 1 , z 1 , x 2 , y 2 , z 2 , asupra căruia se impun o restricție și o legătură, exprimate matematic sub forma unei ecuații:

Din punct de vedere fizic, aceasta înseamnă că distanța dintre punctele materiale este întotdeauna l.În acest caz, numărul de grade de libertate este 5. Exemplul considerat este un model al unei molecule diatomice.

Trei puncte de material 1, 2 și 3 sunt conectate rigid între ele. prieten. Nouă coordonate caracterizează poziția unui astfel de sistem: x1, y1, z1, x2, y2, z2, x 3, y 3 , z 3 . Cu toate acestea, trei conexiuni între puncte determină independența doar a șase coordonate. Sistemul are șase grade de libertate. Deoarece poziția a trei puncte care nu se află pe o singură linie dreaptă determină în mod unic poziția unui corp rigid, corpul rigid are și șase grade de libertate.

Moleculele triatomice și poliatomice au același număr de grade de libertate (șase) dacă aceste molecule sunt considerate formațiuni rigide.

1 Dacă pentru coordonata dependentă din (5.44) se obține o valoare imaginară, aceasta înseamnă că coordonatele independente alese nu corespund niciunui punct situat pe o sferă cu o rază dată.

În moleculele poliatomice reale, atomii sunt în mișcări oscilatorii, astfel încât numărul de grade de libertate ale unor astfel de molecule este mai mare de șase.

Numărul de grade de libertate determină nu numai numărul de variabile independente care caracterizează poziția sistemului mecanic, ci și, ceea ce este foarte important, numărul de deplasări independente ale sistemului. Astfel, trei grade de libertate ale unui punct material liber înseamnă că orice deplasare a unui punct poate fi descompusă în deplasări independente de-a lungul a trei axe de coordonate. Deoarece un punct nu are dimensiuni, nu are sens să vorbim despre rotația lui. Deci, un punct material are trei grade de libertate de mișcare de translație. Un punct material de pe un plan, sferă sau altă suprafață are două grade de libertate de mișcare de translație. Mișcarea unui punct material de-a lungul unei curbe (un exemplu condiționat este deplasarea unui tren de-a lungul șinelor) corespunde unui grad de libertate de mișcare de translație.

Un corp rigid care se rotește în jurul unei axe fixe are un grad de libertate de mișcare de rotație. Roata trenului are două grade de libertate: unul este de rotație, iar celălalt este de translație (deplasarea axei roții de-a lungul șinei). Șase grade de libertate ale unui corp rigid înseamnă că orice deplasare a acestui corp poate fi descompusă în componente: deplasarea centrului de masă este descompusă în trei mișcări de translație de-a lungul axelor de coordonate, iar rotația constă în trei rotații mai simple în jurul coordonatei. axele care trec prin centrul de masă.

Pe fig. 5.18-5.20 prezintă îmbinări cu balamale corespunzătoare unui, două și trei grade de libertate.

Orez. 5.18

Orez. 5.19

Orez. 5.20

5.6. CENTRIFUGARE

Centrifugarea este procesul de separare (separare) a sistemelor neomogene, precum particulele din lichidele în care se află, datorită rotației lor.

Luați în considerare separarea sistemelor neomogene în câmpul gravitațional. Să presupunem că există o suspensie apoasă de particule de diferite densități. În timp, datorită acțiunii gravitației și a flotabilității F A are loc stratificarea particulelor: particule cu o densitate mai mare decât cea a chiuvetei de apă, particule cu o densitate mai mică decât cea a apei plutitoare. Forța rezultată care acționează, de exemplu, asupra unei particule individuale mai dense este:

Unde ρ 1 este densitatea substanței particulei; ρ este densitatea apei; V este volumul particulei.

Dacă valorile lui ρ 1 și ρ diferă puțin unele de altele, atunci forța Fp este mic iar separarea (depunerea) are loc destul de lent. Într-o centrifugă (separator) o astfel de separare este efectuată forțat prin rotirea mediului de separat.

Luați în considerare fizica acestui fenomen.

Lăsați volumul de lucru al centrifugei (Fig. 5.21: a - aspect; b - schema volumului de lucru) să fie complet ocupat de orice lichid omogen. Selectați mental un volum mic V acest lichid, situat la distanță r de pe axa de rotație OO". Cu rotația uniformă a centrifugei pe volumul selectat, pe lângă forța gravitațională și de flotabilitate, care se echilibrează reciproc, acționează o forță centripetă. Aceasta este o forță din partea lichidului care înconjoară volumul. Este îndreptată în mod natural către axa de rotație și este egală cu:

Unde ρ este densitatea lichidului.

Să presupunem acum că volumul alocat V este o particulă separată, a cărei densitate a substanței este ρ 1 (ρ 1 Φ ρ). Forța care acționează asupra particulei din partea fluidului înconjurător nu se va modifica, așa cum se poate observa din formula (5.45).

Pentru ca particula să se rotească împreună cu lichidul, asupra acesteia trebuie să acționeze o forță centripetă, egală cu:

Unde m 1 este masa particulei, iar ρ 1 este densitatea corespunzătoare acesteia.

Orez. 5.21

Dacă F> F1, apoi particula se deplasează spre axa de rotație. Dacă F< F1, atunci impactul asupra particulei din lichid nu va fi suficient pentru a o menține pe o traiectorie circulară, iar particula va începe să se miște la periferie prin inerție. Efectul de separare este determinat de forța în exces F, acționând din partea lichidului asupra particulei selectate, peste valoarea forței centripete F 1, care determină mișcarea într-un cerc:

Această expresie arată că efectul centrifugării este mai mare, cu atât diferența dintre densitățile particulelor separate și lichidul este mai mare și, de asemenea, depinde în mod semnificativ de viteza unghiulară de rotație 1 .

Comparați separarea prin centrifugare cu separarea gravitațională:

1 Gravitația și flotabilitatea nu sunt luate în considerare la derivarea formulei (5.47), deoarece acestea sunt direcționate de-a lungul axei de rotație și nu au un efect fundamental asupra centrifugării.

Ultracentrifugele sunt capabile să separe particulele mai mici de 100 nm suspendate sau dizolvate într-un lichid. Ei au găsit o largă aplicație în cercetarea biomedicală pentru separarea biopolimerilor, virușilor și particulelor subcelulare.

Viteza de separare este deosebit de importantă în cercetarea biologică și biofizică, deoarece starea obiectelor studiate se poate schimba semnificativ în timp.

Să presupunem că un corp rigid A (Fig. 1.19, a) se poate roti în jurul unei axe fixe. Pentru a provoca rotația corpului (pentru a-i schimba viteza unghiulară), este necesară o influență externă. Cu toate acestea, forța a cărei direcție trece prin axa de rotație, sau forța paralelă cu axa, nu poate modifica viteza unghiulară a corpurilor.

Prin urmare, din forța externă aplicată corpului, este necesar să se selecteze componente care nu provoacă rotație. Rotația poate fi cauzată numai de o forță (forța de rotație) situată într-un plan perpendicular pe axa de rotație și îndreptată tangențial la cercul descris de punctul de aplicare a acestuia.

Rețineți că atunci când corpul se rotește, componentele muncii nu funcționează, deoarece punctul de aplicare a acestor forțe se mișcă perpendicular pe direcțiile lor. Munca este efectuată numai de forța de rotație; este proiecția forței care acționează asupra corpului pe direcția de mișcare a punctului de aplicare a acestei forțe.

Să determinăm cantitatea de lucru pe care o efectuează forța de rotație dacă punctul de aplicare a acesteia este deplasat de-a lungul unui cerc de rază cu (Fig. 1.19, b). Să presupunem că mărimea forței rămâne constantă. Apoi

Produsul forței de rotație și razei este momentul forței de rotație sau cuplul care acționează asupra corpului dat și este notat cu condus din forța specificată.

axa faţă de direcţia forţei). Astfel, în formula (2.8)

prin urmare, munca efectuată de cuplul este egal cu produsul acestui moment cu unghiul de rotație al corpului:

Dacă cuplul (forța sau umărul său) se modifică în timp, atunci munca efectuată este definită ca suma:

Momentul forței de rotație este reprezentat ca un vector care coincide cu axa de rotație; orientarea pozitivă a acestui vector se alege în direcția în care s-ar deplasa șurubul drept rotit de acest moment.

Cuplul aplicat corpului îi conferă o oarecare accelerație unghiulară în funcție de direcțiile vectorilor pe care i-am ales, aceștia fiind orientați de-a lungul axei de rotație în același sens. Relația dintre mărimea cuplului și mărimea accelerației unghiulare raportate de acesta poate fi stabilită în două moduri:

a) puteți folosi faptul că munca forței motrice este egală cu modificarea energiei cinetice a corpului căruia i se aplică această forță: Pentru un corp în rotație, conform formulelor (2.9) și (2.4), avem avea

Aici presupunem că momentul de inerție al corpului nu se modifică în timpul rotației. Împărțind această ecuație și reducând cu obținem

b) puteți folosi faptul că momentul forței de rotație este egal cu suma momentelor forțelor care imprimă accelerații tangenţiale părților componente individuale ale corpului, aceste forțe sunt egale și momentele lor -

Să înlocuim accelerațiile tangențiale cu accelerația unghiulară, care este aceeași pentru toate particulele unui corp în rotație (dacă corpul nu se deformează în timpul rotației): Atunci

Formula (2.12) exprimă legea de bază a dinamicii mișcării de rotație a corpurilor solide (nedeformabile), pentru care

accelerația unghiulară dobândită de un corp sub acțiunea unui cuplu dat este direct proporțională cu mărimea acestui moment și invers proporțională cu momentul de inerție al corpului în jurul axei de rotație:

În formă vectorială, această lege este scrisă ca

Dacă corpul este deformat în timpul rotației, atunci momentul său de inerție față de axa de rotație se va modifica. Imaginați-vă mental un corp rotativ format din multe părți elementare (punctuale); atunci deformarea întregului corp va însemna o modificare a distanțelor de la aceste părți ale corpului până la axa de rotație. Cu toate acestea, o modificare a distanței unei viteze unghiulare date de rotație ω va fi însoțită de o modificare a vitezei liniare a acestei particule și, prin urmare, a energiei sale cinetice. Astfel, la o viteză unghiulară constantă de rotație a corpului, o modificare a distanțelor (deci, o modificare a momentului de inerție al corpului) va fi însoțită de o modificare a energiei cinetice de rotație a întregului corp.

Din formula (2.4), dacă presupunem variabile, putem obține

Primul termen arată modificarea energiei cinetice a corpului în rotație, care a avut loc numai ca urmare a unei modificări a vitezei unghiulare de rotație (la un moment dat de inerție a corpului), iar al doilea termen arată modificarea în energie cinetică, care a apărut doar ca urmare a unei modificări a momentului de inerție a corpului (la o viteză unghiulară dată de rotație).

Cu toate acestea, atunci când distanța de la corpul punctual la axa de rotație se modifică, forțele interne care leagă acest corp de axa de rotație vor funcționa: negative dacă corpul se îndepărtează și pozitive dacă corpul se apropie de axa de rotație; această lucrare poate fi calculată dacă presupunem că forța care leagă particulele de axa de rotație este numeric egală cu forța centripetă:

Pentru întregul corp, format din multe particule cu mase, obținem

În cazul general, când un cuplu extern acționează asupra unui corp, modificarea energiei cinetice trebuie echivalată cu suma a două lucrări: cuplul extern și forțele interne.La rotație accelerată, mărimile vor avea semne pozitive, - negative.

semn (deoarece particulele corpului se îndepărtează de axa de rotație); Apoi

Înlocuind aici valoarea din expresia (2.15) și înlocuind cu se obține

sau după reducere

Aceasta este o vedere generală a legii de bază a mecanicii pentru corpurile care se rotesc în jurul unei axe fixe; este aplicabilă și corpurilor care se deformează. La , formula (2.16) trece în formula (2.14).

Rețineți că pentru corpurile deformate, o modificare a vitezei unghiulare de rotație este posibilă chiar și în absența unui cuplu extern. Într-adevăr, ca - din formula (2.16) obținem:

În acest caz, viteza unghiulară de rotație ω se modifică numai datorită unei modificări a momentului de inerție a corpului cauzată de forțele interne.

Noțiuni de bază.

Moment de putere raportat la axa de rotație este produsul vectorial al vectorului rază de forță.

(1.14)

Momentul forței este un vector , a cărei direcție este determinată de regula ghișeului (șurubul din dreapta), în funcție de direcția forței care acționează asupra corpului. Momentul de forță este direcționat de-a lungul axei de rotație și nu are un punct de aplicare anume.

Valoarea numerică a acestui vector este determinată de formula:

M=r F păcat (1.15),

unde  - unghiul dintre vectorul rază și direcția forței.

Dacă =0 sau  , moment de putere M=0, adică forța care trece prin axa de rotație sau care coincide cu aceasta nu provoacă rotație.

Cel mai mare moment de cuplu este creat dacă forța acționează la un unghi  =  /2 (M 0) sau  =3  /2 (M 0).

Folosind conceptul de umăr de forță (umăr de forță d este o perpendiculară căzută de la centrul de rotație la linia de acțiune a forței), formula pentru momentul forței ia forma:

, Unde
(1.16)

Regulă de moment al forței(condiție de echilibru pentru un corp cu o axă fixă ​​de rotație):

Pentru ca un corp cu axa fixa de rotatie sa fie in echilibru, este necesar ca suma algebrica a momentelor fortelor care actioneaza asupra acestui corp sa fie egala cu zero.

 M i =0 (1.17)

Unitatea SI a momentului de forta este [Nm]

În timpul mișcării de rotație, inerția unui corp depinde nu numai de masa sa, ci și de distribuția sa în spațiu față de axa de rotație.

Inerția în timpul rotației este caracterizată de momentul de inerție al corpului față de axa de rotație J.

Moment de inerție a unui punct material în raport cu axa de rotație este o valoare egală cu produsul dintre masa punctului și pătratul distanței acestuia față de axa de rotație:

J  =m   r  2 (1.18)

Momentul de inerție al corpului față de axă este suma momentelor de inerție ale punctelor materiale care alcătuiesc corpul:

J= m   r  2 (1.19)

Momentul de inerție al unui corp depinde de masa și forma acestuia, precum și de alegerea axei de rotație. Pentru a determina momentul de inerție al unui corp în jurul unei anumite axe, se folosește teorema Steiner-Huygens:

J=J 0 +m d 2 (1.20),

Unde J 0 – moment de inerție în jurul unei axe paralele care trece prin centrul de masă al corpului, d – distanța dintre două axe paralele . Momentul de inerție în SI se măsoară în [kgm 2]

Momentul de inerție în timpul mișcării de rotație a trunchiului uman este determinat empiric și calculat aproximativ după formulele pentru un cilindru, o tijă rotundă sau o minge.

Momentul de inerție al unei persoane față de axa verticală de rotație, care trece prin centrul de masă (centrul de masă al corpului uman se află în planul sagital puțin înaintea celei de-a doua vertebre sacrale), în funcție de poziția persoana, are următoarele valori: la atenţie - 1,2 kg m 2; cu ipostaza „arabesc” - 8 kgm 2; în poziție orizontală - 17 kg  m 2.

Lucrați în mișcare rotativă apare atunci când un corp se rotește sub acțiunea unor forțe externe.

Lucrul elementar al forței în mișcarea de rotație este egal cu produsul dintre momentul forței și unghiul elementar de rotație al corpului:

dA  =M   d (1.21)

Dacă asupra corpului acționează mai multe forțe, atunci munca elementară a rezultantei tuturor forțelor aplicate este determinată de formula:

dA=M d (1.22),

Unde M- momentul total al tuturor fortelor externe care actioneaza asupra corpului.

Energia cinetică a unui corp în rotațieW La depinde de momentul de inerție al corpului și de viteza unghiulară de rotație a acestuia:

(1.23)

Moment unghiular (moment de impuls) – o cantitate egală numeric cu produsul dintre impulsul corpului și raza de rotație.

L=p r=m V r (1.24).

După transformările corespunzătoare, puteți scrie formula pentru determinarea momentului unghiular sub forma:

(1.25).

impuls unghiular este un vector a cărui direcție este determinată de regula șurubului drept. Unitatea de măsură a momentului unghiular în SI este kgm 2 /s

Legile de bază ale dinamicii mișcării de rotație.

Ecuația de bază pentru dinamica mișcării de rotație:

Accelerația unghiulară a unui corp în rotație este direct proporțională cu momentul total al tuturor forțelor externe și invers proporțională cu momentul de inerție al corpului.

(1.26).

Această ecuație joacă același rol în descrierea mișcării de rotație ca a doua lege a lui Newton pentru mișcarea de translație. Din ecuație se poate observa că sub acțiunea forțelor externe, accelerația unghiulară este cu atât mai mare, cu atât momentul de inerție al corpului este mai mic.

A doua lege a lui Newton pentru dinamica mișcării de rotație poate fi scrisă într-o formă diferită:

(1.27),

acestea. prima derivată a momentului unghiular al corpului în raport cu timpul este egală cu momentul total al tuturor forțelor externe care acționează asupra acestui corp.

Legea conservării impulsului corpului:

Dacă momentul total al tuturor forțelor externe care acționează asupra corpului este zero, adică.

 M  =0 , Apoi dL/dt=0 (1.28).

Prin urmare
sau
(1.29).

Această afirmație este esența legii conservării momentului unghiular al corpului, care este formulată după cum urmează:

Momentul unghiular al unui corp rămâne constant dacă momentul total al forțelor externe care acționează asupra unui corp în rotație este zero.

Această lege este valabilă nu numai pentru un corp absolut rigid. Un exemplu este un patinator care efectuează o rotație în jurul unei axe verticale. Prin apăsarea mâinilor, patinatorul reduce momentul de inerție și crește viteza unghiulară. Pentru a încetini rotația, dimpotrivă, își întinde brațele larg; ca urmare, momentul de inerție crește și viteza unghiulară de rotație scade.

În concluzie, oferim un tabel comparativ al principalelor mărimi și legi care caracterizează dinamica mișcărilor de translație și rotație.

Tabelul 1.4.

Fie ca un corp, sub acțiunea unei forțe F aplicată în punctul A, să intre în rotație în jurul axei OO" (Fig. 1.14).

Forța acționează într-un plan perpendicular pe axă. Perpendiculara p, coborâtă din punctul O (care se află pe axă) pe direcția forței, se numește umărul puterii. Produsul forței asupra umărului determină modulul momentului de forță relativ la punctul O:

M = Fp=Frsina.

Moment de putere este un vector determinat de produsul vectorial dintre raza-vector al punctului de aplicare a forței și vectorul forță:

(3.1) Unitatea de măsură a momentului de forță este newtonmetrul (N m).

Direcția M poate fi găsită folosind regula cu șurub potrivită.

impuls unghiular particula se numește produsul vectorial dintre vectorul razei particulei și impulsul acesteia:

sau în formă scalară L = gPsinα

Această mărime este vectorială și coincide în direcția cu vectorii ω.

§ 3.2 Momentul de inerție. teorema lui Steiner

O măsură a inerției corpurilor aflate în mișcare de translație este masa. Inerția corpurilor în timpul mișcării de rotație depinde nu numai de masă, ci și de distribuția acesteia în spațiu față de axa de rotație. Măsura inerției în timpul mișcării de rotație este o mărime numitămomentul de inerție al corpului despre axa de rotație.

Momentul de inerție al unui punct material raportat la axa de rotație este produsul dintre masa acestui punct și pătratul distanței acestuia față de axă:

I i =m i r i 2 (3.2)

Momentul de inerție al corpului față de axa de rotație Numiți suma momentelor de inerție ale punctelor materiale care alcătuiesc acest corp:

(3.3)

În cazul general, dacă corpul este solid și este o colecție de puncte cu mase mici dm, momentul de inerție este determinat prin integrare:

(3.4)

Dacă corpul este omogen şi densitatea lui
, apoi momentul de inerție al corpului

(3.5)

Momentul de inerție al unui corp depinde de ce axă se rotește și de modul în care masa corpului este distribuită pe volum.

Momentul de inerție al corpurilor care au forma geometrică corectă și o distribuție uniformă a masei în volum este cel mai simplu determinat.

Momentul de inerție al unei tije omogene faţă de axa care trece prin centrul de inerţie şi perpendicular pe tijă

(3.6)

Momentul de inerție al unui cilindru omogenîn jurul unei axe perpendiculare pe baza ei și care trece prin centrul de inerție,

(3.7)

Momentul de inerție al unui cilindru cu pereți subțiri sau un cerc în jurul unei axe perpendiculare pe planul bazei sale și care trece prin centrul său,

(3.8)

Moment de inerție bila raportat la diametru

(3.9)

Luați în considerare un exemplu . Să determinăm momentul de inerție al discului în jurul axei care trece prin centrul de inerție și perpendicular pe planul de rotație. Masa discului - m, raza - R.

Zona inelului (Fig. 3.2), închisă între

r și r + dr este egal cu dS = 2πr dr . Aria discului S = πR 2 .

Prin urmare,
. Apoi

sau

Conform

Formulele date pentru momentele de inerție ale corpurilor sunt date cu condiția ca axa de rotație să treacă prin centrul de inerție. Pentru a determina momentele de inerție ale unui corp în jurul unei axe arbitrare, ar trebui să folosiți teorema lui Steiner : momentul de inerție al corpului față de o axă de rotație arbitrară este egal cu suma momentului de inerție al corpului față de o axă paralelă cu cea dată și care trece prin centrul de masă al corpului și produsul dintre masa corpului după pătratul distanței dintre axe:

(3.11)

Unitatea de măsură a momentului de inerție este un kilogram-metru pătrat (kg m 2).

Deci, momentul de inerție al unei tije omogene în jurul axei care trece prin capătul ei, conform teoremei lui Steiner, este egal cu

(3.12)

Acest subiect va fi dedicat luării în considerare a unui tip special de forțe - forțele de inerție. Particularitatea acestor forțe este următoarea. Toate forțele mecanice - fie forțele gravitaționale, de interacțiune elastică sau forțele de frecare - apar atunci când corpul este afectat de alte corpuri. Cu forțele de inerție, situația este diferită.

În primul rând, să ne amintim ce este inerția. Inerția este un fenomen fizic, constând în faptul că organismul se străduiește mereu să-și mențină viteza inițială. Și forțele de inerție apar atunci când viteza corpului se schimbă - adică. are loc accelerația. În funcție de mișcarea la care ia parte corpul, acesta are una sau alta accelerație și generează una sau alta forță de inerție. Dar toate aceste forțe sunt unite după același model: forţa de inerţie este întotdeauna îndreptată opus acceleraţiei care a generat-o.

Prin natura lor, forțele inerțiale sunt diferite de alte forțe mecanice. Toate celelalte forțe mecanice apar ca urmare a acțiunii unui corp asupra altuia. În timp ce forțele de inerție se datorează proprietăților mișcării mecanice a corpului. Apropo, în funcție de mișcarea în care este implicat corpul, apare una sau alta forță de inerție:

Mișcarea poate fi simplă și apoi vom vorbi despre forța de inerție a mișcării de translație;

Mișcarea poate fi curbilinie și apoi vom vorbi despre forța centrifugă de inerție;

În cele din urmă, mișcarea poate fi atât dreaptă cât și curbilinie (dacă corpul se mișcă într-un sistem rotativ sau se mișcă în timp ce se rotește), iar atunci vom vorbi despre despre forța Coriolis.

Să luăm în considerare mai detaliat tipurile de forțe inerțiale și condițiile de apariție a acestora.

1. FORŢĂ DE INERTIE A MIŞCĂRII DE TRANSLAŢIE F i . Apare atunci când un corp se mișcă pe o cale dreaptă. Ne confruntăm constant cu acțiunea acestei forțe în vehiculele care se deplasează pe un drum drept, la frânare și la accelerare. La frânare suntem aruncați înainte, pentru că. viteza de mișcare scade brusc, iar corpul nostru încearcă să mențină viteza pe care o avea. Când luăm viteză, suntem apăsați în spătarul scaunului din același motiv. Pe fig. 2.1

Direcțiile de accelerație și forțele inerțiale ale mișcării de translație sunt prezentate în cazul scăderii vitezei: accelerația este direcționată opus mișcării, iar forța de inerție este îndreptată opus accelerației. Formula forței de inerție este dată de a doua lege a lui Newton: . Semnul minus se datorează faptului că vectorii și au direcții opuse. Valoarea numerică (modulul) acestei forțe se calculează, respectiv, prin formula:

F=ma (3.1)

2. FORTA CENTRIFUGA DE INERTIE F i . Pentru a înțelege cum apare această forță, luați în considerare Fig. 3.2, care prezintă un disc care se rotește într-un plan orizontal, cu o bilă atașată la centrul discului prin intermediul unei legături de tracțiune (cum ar fi o bandă de cauciuc). Când discul începe să se rotească, mingea tinde să se îndepărteze de

centrați și strângeți elasticul. În plus, cu cât discul se rotește mai repede, cu atât mingea se deplasează mai departe de centrul discului. O astfel de mișcare a bilei de-a lungul planului discului se datorează acțiunii unei forțe numite forța centrifugă de inerție (F cb) . Prin urmare, forta centrifuga apare in timpul rotatiei si este indreptata de-a lungul razei de la centrul de rotatie.F cb este forța de inerție, ceea ce înseamnă că apariția ei se datorează prezenței accelerației, care ar trebui direcționată opus acestei forțe. Dacă forța centrifugă este îndreptată departe de centru, atunci este evident că cauza acestei forțe este accelerația normală (centripetă). un n , deoarece este cea care este îndreptată spre centrul de rotație (vezi Subiectul 1, §1.2, punctul 3). Pe baza acesteia, obținem formula forței centrifuge. Conform celei de-a doua legi a lui Newton F=ma , Unde m - masa corpului. Atunci pentru forța centrifugă de inerție relația este adevărată:

F cb \u003d ma n.

Ținând cont de (1.18) și (1.19), obținem:

(3.2) și F cb \u003d mω 2 r (3.3).

3. CORIOLIS FORCE F K . Când sunt combinate două tipuri de mișcare: de rotație și de translație, apare o altă forță, numită forța Coriolis (sau forța Coriolis) numit după mecanicul francez Gustave Gaspard Coriolis (1792-1843), care a dat calculul acestei forțe.

Apariția forței Coriolis poate fi detectată prin exemplul experimentului prezentat în Fig. 3.3. Înfățișează un disc care se rotește pe orizontală

Orez. 3.3 vedere de sus

avioane. Să desenăm o linie dreaptă radială OA pe disc și să lansăm o minge cu viteza v în direcția de la O la A. Dacă discul nu se rotește, mingea se va rostogoli de-a lungul liniei drepte trasate de noi. Dacă discul este adus în rotație în direcția indicată de săgeată, atunci mingea se va rostogoli de-a lungul curbei OB indicată de linia punctată, iar viteza sa υ își va schimba direcția (vezi Fig. 3.3 (b)). În consecință, în raport cu cadrul de referință rotativ (și în acest caz este un disc), bila se comportă ca și cum ar fi acționată asupra ei de o forță perpendiculară pe viteza υ. Aceasta este forța Coriolis. F K . Ea este cea care face ca mingea să devieze de la traiectoria rectilinie OA. Formula care descrie această forță este din nou determinată de a doua lege a lui Newton, doar că de această dată așa-numita Accelerația Coriolis K : ,F K =2mυω (3,5).

Deci, așa cum am menționat deja, pentru ca forța Coriolis să se manifeste, este necesar să combinați 2 tipuri de mișcare. Și aici există două opțiuni: 1). Corpul se mișcă în raport cu cadrul de referință rotativ. Acest caz este prezentat în Figura 3.3. 2). Un corp rotativ se deplasează înainte Un exemplu sunt așa-numitele mingi „răucite” - o tehnică folosită în fotbal - atunci când mingea este lovită astfel încât să se rotească în timpul zborului.