Cosinus pătrat antiderivat x. Integrarea funcţiilor trigonometrice. Integrarea funcţiilor trigonometrice complexe

Sunt luate în considerare în detaliu exemple de soluții de integrale pe părți, al căror integrand este produsul unui polinom și o exponențială (e la puterea lui x) sau un sinus (sin x) sau un cosinus (cos x).

Conţinut

Vezi si: Metoda de integrare pe părți
Tabelul integralelor nedefinite
Metode de calcul a integralelor nedefinite
Funcții elementare de bază și proprietățile lor

Formula de integrare prin părți

La rezolvarea exemplelor din această secțiune se folosește formula de integrare pe părți:
;
.

Exemple de integrale care conțin produsul unui polinom și sin x, cos x sau e x

Iată exemple de astfel de integrale:
, , .

Pentru a integra astfel de integrale, polinomul se notează cu u, iar restul cu v dx . În continuare, se aplică formula de integrare pe părți.

Mai jos este o soluție detaliată a acestor exemple.

Exemple de rezolvare a integralelor

Exemplu cu exponent, e la puterea lui x

Definiți integrala:
.

Introducem exponentul sub semnul diferential:
e - x dx = - e - x d(-x) = - d(e - x).

Ne integrăm pe părți.

Aici
.
Integrala rămasă este, de asemenea, integrabilă prin părți.
.
.
.
În sfârșit avem:
.

Un exemplu de definire a unei integrale cu un sinus

Calculați integrala:
.

Introducem sinusul sub semnul diferenţialului:

Ne integrăm pe părți.

aici u = x 2 , v = cos(2x+3), du = ( x2 )′ dx

Integrala rămasă este, de asemenea, integrabilă prin părți. Pentru a face acest lucru, introducem cosinusul sub semnul diferenţialului.


aici u = x, v = sin(2x+3), du = dx

În sfârșit avem:

Un exemplu de produs al unui polinom și al cosinusului

Calculați integrala:
.

Introducem cosinusul sub semnul diferenţialului:

Ne integrăm pe părți.

aici u = x 2+3x+5, v = sin2x, du = ( x 2 + 3 x + 5 )′ dx

În practică, de multe ori trebuie să se calculeze integrale ale funcțiilor transcendentale care conțin funcții trigonometrice. În cadrul acestui material, vom descrie principalele tipuri de integranți și vom arăta ce metode pot fi utilizate pentru a le integra.

Integrarea sinusului, cosinusului, tangentei și cotangentei

Să începem cu metodele de integrare a principalului funcții trigonometrice– sin , cos , t g , c t g . Folosind tabelul cu antiderivate, notăm imediat că ∫ sin x d x \u003d - cos x + C și ∫ cos x d x \u003d sin x + C.

Pentru a calcula integralele nedefinite ale funcțiilor t g și c t g, puteți folosi suma sub semnul diferențial:

∫ tgxdx = ∫ sin x cos xdx = d (cos x) = - sin xdx = = - ∫ d (cos x) cos x = - ln cos x + C ∫ ctgxdx = ∫ cos x sin xdx = d (sin x) = cos xdx = = ∫ d (sin x) sin x = ln sin x + C

Cum am obținut formulele ∫ d x sin x \u003d ln 1 - cos x sin x + C și ∫ d x cos x \u003d ln 1 + sin x cos x + C, luate din tabelul cu antiderivate? Să explicăm un singur caz, deoarece al doilea va fi clar prin analogie.

Folosind metoda substituției, scriem:

∫ d x sin x = sin x = t ⇒ x = a r c sin y ⇒ d x = d t 1 - t 2 = d t t 1 - t 2

Aici trebuie să integrăm funcția irațională. Luăm aceeași metodă de înlocuire:

∫ dtt 1 - t 2 = 1 - t 2 = z 2 ⇒ t = 1 - z 2 ⇒ dt = - zdz 1 - z 2 = = ∫ - zdzz 1 - z 2 1 - z 2 = ∫ dzz 2 - 1 = ∫ dz (z - 1) (z +) = = 1 2 ∫ dzz - 1 - 1 2 ∫ dzz + 1 = 1 2 ln z - 1 - 1 2 z + 1 + C = = 1 2 ln z - 1 z + 1 + C = ln z - 1 z + 1 + C

Acum facem înlocuirea inversă z \u003d 1 - t 2 și t \u003d sin x:

∫ dx sin x = ∫ dtt 1 - t 2 = ln z - 1 z + 1 + C = = ln 1 - t 2 - 1 1 - t 2 + 1 + C = ln 1 - sin 2 x - 1 1 - sin 2 x + 1 + C = = ln cos x - 1 cos x + 1 + C = ln (cos x - 1) 2 sin 2 x + C = = ln cos x - 1 sin x + C

Separat, vom analiza cazuri cu integrale care conțin puteri ale funcțiilor trigonometrice, precum ∫ sin n x d x , ∫ cos n x d x , ∫ d x sin n x , ∫ d x cos n x .

Puteți citi despre cum să le calculați corect în articolul despre integrare folosind formule recursive. Dacă știți cum sunt derivate aceste formule, puteți lua cu ușurință integrale precum ∫ sin n x cos m x d x cu m și n natural.

Dacă avem o combinație de funcții trigonometrice cu polinoame sau funcții exponențiale, atunci acestea vor trebui integrate pe părți. Vă sfătuim să citiți articolul dedicat metodelor de găsire a integralelor ∫ P n (x) sin (ax) dx , ∫ P n (x) cos (ax) dx , ∫ ea x sin (ax) dx , ∫ ea x cos (ax) dx .

Cele mai dificile sunt problemele în care integrandul include funcții trigonometrice cu argumente diferite. Pentru a face acest lucru, trebuie să utilizați formulele de bază ale trigonometriei, așa că este recomandabil să le amintiți pe de rost sau să țineți o evidență la îndemână.

Exemplul 1

Găsiți un set funcții antiderivate y = sin (4 x) + 2 cos 2 (2 x) sin x cos (3 x) + 2 cos 2 x 2 - 1 sin (3 x) .

Soluţie

Folosim formulele de reducere a puterii și scriem că cos 2 x 2 \u003d 1 + cos x 2 și cos 2 2 x \u003d 1 + cos 4 x 2. Mijloace,

y = sin (4 x) + 2 cos 2 (2 x) sin x cos (3 x) + 2 cos 2 x 2 - 1 sin (3 x) = sin (4 x) + 2 1 + cos 4 x 2 sin x cos (3 x) + 2 1 + cos x 2 - 1 sin (3 x) = = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x)

La numitor avem formula pentru sinusul sumei. Apoi o poți scrie așa:

y = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x) = sin (4 x) + cos (4 x) + 1 sin (4 x ) = = 1 + cos (4 x) sin (4 x)

Avem suma a 3 integrale.

∫ sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x) dx = = ∫ dx + cos (4 x) dx sin (4 x) + ∫ dx sin (4 x) = = x + 1 4 ln ∫ d (sin (4 x)) sin (4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) = = 1 4 ln sin ( 4 x) ) + 1 4 ln cos (4 x) - 1 sin (4 x) + C = x + 1 4 ln cos 4 x - 1 + C

În unele cazuri, funcțiile trigonometrice care sunt sub integrală pot fi reduse la fracțional expresii rationale folosind metoda standard de substituție. Mai întâi, să luăm formule care exprimă sin, cos și t g prin tangenta unui semiargument:

sin x = 2 t g x 2 1 + t g 2 x 2 , sin x = 1 - t g 2 x 2 1 + t g 2 x 2 , t g x = 2 t g x 2 1 - t g 2 x 2

De asemenea, va trebui să exprimăm diferența d x în termenii tangentei semiunghiului:

Deoarece d t g x 2 \u003d t g x 2 "d x \u003d d x 2 cos 2 x 2, atunci

d x = 2 cos 2 x 2 d t g x 2 = 2 d t g x 2 1 cos 2 x 2 = 2 d t g x 2 cos 2 x 2 + sin 2 x 2 cos 2 x 2 = 2 d t g x 2 1 + t g 2 x 2

Astfel, sin x \u003d 2 z 1 + z 2, cos x 1 - z 2 1 + z 2, t g x 2 z 1 - z 2, d x \u003d 2 d z 1 + z 2 la z \u003d t g x 2.

Exemplul 2

Aflați integrala nedefinită ∫ d x 2 sin x + cos x + 2 .

Soluţie

Folosim metoda standard de substituție trigonometrică.

2 sin x + cos x + 2 = 2 2 z 1 + z 2 + 1 - z 2 1 + z 2 = z 2 + 4 z + 3 1 + z 2 ⇒ dx 2 sin x + cos x + 2 = 2 dz 1 + z 2 z 2 + 4 z + 3 1 + z 2 = 2 dzz 2 + 4 z + 3

Obținem că ∫ d x 2 sin x + cos x + 2 = 2 d z z 2 + 4 z + 3 .

Acum putem extinde integralul în fracții simple și obținem suma a două integrale:

∫ dx 2 sin x + cos x + 2 = 2 ∫ 2 dzz 2 + 4 z + 3 = 2 ∫ 1 2 1 z + 1 - 1 z + 3 dz = = ∫ dzz + 1 - ∫ C z + 3 = ln z + 1 - log z + 3 + C = log z + 1 z + 3 + C

∫ d x 2 sin x + cos x + 2 = ln z + 1 z + 3 + C = ln t g x 2 + 1 t g x 2 + 3 + C

Răspuns: ∫ d x 2 sin x + cos x + 2 = ln t g x 2 + 1 t g x 2 + 3 + C

Este important de remarcat că acele formule care exprimă funcții în termeni de tangente a unui semiargument nu sunt identități, prin urmare, expresia rezultată ln tgx 2 + 1 tgx 2 + 3 + C este mulțimea de antiderivate ale funcției y = 1 2 sin x + cos x + 2 numai pe domeniul definiției.

Pentru a rezolva alte tipuri de probleme, puteți utiliza metodele de bază de integrare.

Dacă observați o greșeală în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter

Integrale complexe

Acest articol completează subiectul integralelor nedefinite și include integrale pe care le consider destul de dificile. Lecția a fost creată la solicitarea repetată a vizitatorilor care și-au exprimat dorința ca pe site să fie analizate exemple mai dificile.

Se presupune că cititorul acestui text este bine pregătit și știe să aplice tehnicile de bază ale integrării. Manichinii și oamenii care nu sunt foarte încrezători în integrale ar trebui să se refere la prima lecție - Integrală nedefinită. Exemple de soluții unde poți învăța subiectul aproape de la zero. Studenții mai experimentați se pot familiariza cu tehnicile și metodele de integrare, care nu au fost încă întâlnite în articolele mele.

Ce integrale vor fi luate în considerare?

În primul rând, luăm în considerare integralele cu rădăcini, pentru soluția cărora o folosim succesiv substituție variabilăȘi integrare pe părți. Adică, într-un exemplu, două metode sunt combinate simultan. Și încă mai mult.

Apoi ne vom familiariza cu un interesant și original metoda de reducere a integralei la sine. Nu atât de puține integrale sunt rezolvate în acest fel.

Al treilea număr al programului va fi integrale ale fracțiilor complexe, care au trecut peste casa de marcat în articolele anterioare.

În al patrulea rând, vor fi analizate integrale suplimentare din funcțiile trigonometrice. În special, există metode care evită înlocuirea trigonometrică universală, consumatoare de timp.

(2) În integrand, împărțim numărătorul la numitor termen cu termen.

(3) Folosim proprietatea de liniaritate a integralei nedefinite. În ultima integrală, imediat aduceți funcția sub semnul diferenţialului.

(4) Luăm integralele rămase. Rețineți că puteți utiliza paranteze în logaritm și nu în modul, deoarece .

(5) Efectuăm substituția inversă, exprimând din substituția directă „te”:

Studenții masochiști pot diferenția răspunsul și pot obține integrandul original, așa cum tocmai am făcut eu. Nu, nu, am făcut verificarea în sensul corect =)

După cum puteți vedea, în cursul soluției, au trebuit folosite chiar și mai mult de două metode de soluție, așa că pentru a face față unor astfel de integrale, aveți nevoie de abilități de integrare încrezătoare și nu cea mai mică experiență.

În practică, desigur, rădăcina pătrată este mai comună, iată trei exemple pentru o soluție independentă:

Exemplul 2

Aflați integrala nedefinită

Exemplul 3

Aflați integrala nedefinită

Exemplul 4

Aflați integrala nedefinită

Aceste exemple sunt de același tip, astfel încât soluția completă de la sfârșitul articolului va fi doar pentru Exemplul 2, în Exemplele 3-4 - un singur răspuns. Ce înlocuitor să folosiți la începutul deciziilor cred că este evident. De ce am ales același tip de exemple? Deseori găsite în rolurile lor. Mai des, poate, doar ceva de genul .

Dar nu întotdeauna, atunci când rădăcina unei funcții liniare se află sub arc tangentă, sinus, cosinus, exponent și alte funcții, trebuie aplicate mai multe metode simultan. Într-un număr de cazuri, este posibil să „coborâți ușor”, adică imediat după înlocuire, se obține o integrală simplă, care este luată elementar. Cea mai ușoară dintre sarcinile propuse mai sus este Exemplul 4, în care, după înlocuire, se obține o integrală relativ simplă.

Metoda de reducere a integralei la sine

Metodă inteligentă și frumoasă. Să aruncăm o privire la clasicii genului:

Exemplul 5

Aflați integrala nedefinită

Există un binom pătrat sub rădăcină, iar atunci când încercați să integrați acest exemplu, ceainicul poate suferi ore întregi. O astfel de integrală este luată pe părți și se reduce la ea însăși. În principiu, nu este dificil. Dacă știi cum.

Să notăm integrala considerată printr-o literă latină și să începem soluția:

Integrarea pe părți:

(1) Pregătim integrantul pentru împărțirea termen cu termen.

(2) Împărțim termenul integrand cu termen. Poate că nu toată lumea înțelege, voi scrie mai detaliat:

(3) Folosim proprietatea de liniaritate a integralei nedefinite.

(4) Luăm ultima integrală (logaritmul „lung”).

Acum să ne uităm la începutul soluției:

Iar pentru final:

Ce s-a întâmplat? Ca urmare a manipulărilor noastre, integrala s-a redus la sine!

Echivalează începutul și sfârșitul:

Ne transferăm în partea stângă cu o schimbare de semn:

Și dărâmăm zeul în partea dreaptă. Ca rezultat:

Constanta, strict vorbind, ar fi trebuit adăugată mai devreme, dar am adăugat-o la sfârșit. Recomand cu tărie să citiți care este severitatea aici:

Notă: Mai strict, etapa finală a soluției arată astfel:

În acest fel:

Constanta poate fi redenumită cu . De ce poți redenumi? Pentru că mai trebuie orice valori, iar în acest sens nu există nicio diferență între constante și.
Ca rezultat:

Un truc similar cu redenumirea constantă este utilizat pe scară largă în ecuatii diferentiale. Și acolo voi fi strict. Și aici astfel de libertăți sunt permise de mine doar pentru a nu te confunda cu lucruri inutile și a te concentra pe însăși metoda de integrare.

Exemplul 6

Aflați integrala nedefinită

O altă integrală tipică pentru soluție independentă. Soluție completă și răspuns la sfârșitul lecției. Diferența cu răspunsul din exemplul anterior va fi!

Dacă sub rădăcina pătrată există un trinom pătrat, atunci soluția se reduce în orice caz la cele două exemple analizate.

De exemplu, luați în considerare integrala . Tot ce trebuie să faci este în avans selectați un pătrat complet:
.
În continuare, se efectuează o înlocuire liniară, care gestionează „fără consecințe”:
, rezultând o integrală . Ceva familiar, nu?

Sau acest exemplu, cu un binom pătrat:
Selectarea unui pătrat complet:
Și, după o înlocuire liniară, obținem integrala, care este rezolvată și de algoritmul deja considerat.

Luați în considerare încă două exemple tipice despre cum să reduceți o integrală la sine:
este integrala exponentului înmulțită cu sinusul;
este integrala exponentului înmulțită cu cosinusul.

În integralele enumerate pe părți, va trebui să integrați deja de două ori:

Exemplul 7

Aflați integrala nedefinită

Integrandul este exponentul înmulțit cu sinusul.

Integram de două ori pe părți și reducem integrala la sine:

Ca rezultat al dublei integrări pe părți, integrala se reduce la sine. Echivalează începutul și sfârșitul soluției:

Ne transferăm în partea stângă cu o schimbare de semn și ne exprimăm integrala:

Gata. Pe parcurs, este de dorit să pieptănați partea dreaptă, adică. scoateți exponentul din paranteze și puneți sinusul și cosinusul între paranteze într-o ordine „frumoasă”.

Acum să revenim la începutul exemplului sau, mai degrabă, la integrarea pe părți:

Căci am desemnat expozantul. Apare întrebarea, exponentul este întotdeauna notat cu ? Nu este necesar. De fapt, în integrala considerată fundamental nu contează, pentru ce să notăm, se poate merge în altă direcție:

De ce este posibil acest lucru? Deoarece exponentul se transformă în sine (când se diferențiază și se integrează), sinusul și cosinusul se transformă reciproc unul în celălalt (din nou, atât la diferențiere, cât și la integrare).

Adică se poate nota și funcția trigonometrică. Dar, în exemplul considerat, acest lucru este mai puțin rațional, deoarece vor apărea fracții. Dacă doriți, puteți încerca să rezolvați acest exemplu în al doilea mod, răspunsurile trebuie să fie aceleași.

Exemplul 8

Aflați integrala nedefinită

Acesta este un exemplu de do-it-yourself. Înainte de a decide, gândiți-vă la ce este mai profitabil să desemnați în acest caz, funcție exponențială sau trigonometrică? Soluție completă și răspuns la sfârșitul lecției.

Și, desigur, nu uitați că majoritatea răspunsurilor din această lecție sunt destul de ușor de verificat prin diferențiere!

Exemplele au fost considerate ca nu cele mai dificile. În practică, integralele sunt mai frecvente, unde constanta este atât în ​​exponent, cât și în argumentul funcției trigonometrice, de exemplu: . Mulți oameni vor trebui să se încurce într-o astfel de integrală, iar eu însumi deseori mă confund. Faptul este că în soluție există o probabilitate mare de apariție a fracțiilor și este foarte ușor să pierzi ceva din cauza neatenției. În plus, există o probabilitate mare de eroare în semne, rețineți că există un semn minus în exponent, iar acest lucru introduce o dificultate suplimentară.

În etapa finală, de multe ori se dovedește ceva de genul:

Chiar și la sfârșitul soluției, ar trebui să fii extrem de atent și să tratați corect fracțiile:

Integrarea fracțiilor complexe

Ne apropiem încet de ecuatorul lecției și începem să luăm în considerare integralele fracțiilor. Din nou, nu toate sunt super complexe, doar dintr-un motiv sau altul, exemplele au fost puțin „off topic” în alte articole.

Continuând tema rădăcinilor

Exemplul 9

Aflați integrala nedefinită

În numitorul de sub rădăcină există un trinom pătrat plus în afara rădăcinii „apendice” sub forma „x”. O integrală a acestei forme este rezolvată folosind o substituție standard.

Noi decidem:

Înlocuirea aici este simplă:

Privind viața după înlocuire:

(1) După înlocuire, reducem termenii de sub rădăcină la un numitor comun.
(2) O scoatem de sub rădăcină.
(3) Reducem numărătorul și numitorul cu . În același timp, sub rădăcină, am rearanjat termenii într-o ordine convenabilă. Cu ceva experiență, pașii (1), (2) pot fi săriți prin efectuarea orală a acțiunilor comentate.
(4) Integrala rezultată, după cum vă amintiți din lecție Integrarea unor fracții, este rezolvată metoda de selecție a pătratului complet. Selectați un pătrat complet.
(5) Prin integrare, obținem un logaritm „lung” obișnuit.
(6) Efectuăm înlocuirea inversă. Dacă inițial , apoi înapoi: .
(7) Acțiunea finală vizează coafarea rezultatului: sub rădăcină, aducem din nou termenii la un numitor comun și îi scoatem de sub rădăcină.

Exemplul 10

Aflați integrala nedefinită

Acesta este un exemplu de do-it-yourself. Aici, se adaugă o constantă la singurul x, iar înlocuirea este aproape aceeași:

Singurul lucru care trebuie făcut suplimentar este să exprimați „x” din înlocuire:

Soluție completă și răspuns la sfârșitul lecției.

Uneori într-o astfel de integrală poate exista un binom pătrat sub rădăcină, asta nu schimbă modul în care se rezolvă soluția, va fi chiar și mai simplu. Simte diferenta:

Exemplul 11

Aflați integrala nedefinită

Exemplul 12

Aflați integrala nedefinită

Scurte soluții și răspunsuri la sfârșitul lecției. Trebuie remarcat faptul că Exemplul 11 ​​este exact integrală binomială, a cărui metodă de rezolvare a fost luată în considerare în lecție Integrale ale funcțiilor iraționale.

Integrală a unui polinom necompunebil de gradul 2 la grad

(polinom la numitor)

O formă mai rară, dar, totuși, care apare în exemple practice a integralei.

Exemplul 13

Aflați integrala nedefinită

Dar să revenim la exemplul cu numărul norocos 13 (sincer, nu am ghicit). Această integrală este și din categoria celor cu care poți suferi destul de mult dacă nu știi să rezolvi.

Soluția începe cu o transformare artificială:

Cred că toată lumea înțelege deja cum se împarte numărătorul la numitor termen cu termen.

Integrala rezultată este luată în părți:

Pentru o integrală de forma ( este un număr natural), am derivat recurent formula de retrogradare:
, Unde este o integrală de grad inferior.

Să verificăm validitatea acestei formule pentru integrala rezolvată.
În acest caz: , , folosim formula:

După cum puteți vedea, răspunsurile sunt aceleași.

Exemplul 14

Aflați integrala nedefinită

Acesta este un exemplu de do-it-yourself. Soluția eșantion utilizează formula de mai sus de două ori consecutiv.

Dacă sub gradul este necompusa trinom pătrat, atunci soluția este redusă la un binom prin extragerea pătratului complet, de exemplu:

Ce se întâmplă dacă există un polinom suplimentar în numărător? În acest caz, se utilizează metoda coeficienților nedeterminați, iar integrandul este extins într-o sumă de fracții. Dar în practica mea a unui astfel de exemplu niciodată întâlnit, așa că am omis acest caz în articol Integrale ale unei funcții fracționale-raționale, îl voi omite acum. Dacă o astfel de integrală încă apare, consultați manualul - totul este simplu acolo. Nu consider oportună includerea materialului (chiar simplu), probabilitatea de întâlnire cu care tinde spre zero.

Integrarea funcţiilor trigonometrice complexe

Adjectivul „dificil” pentru majoritatea exemplelor este din nou în mare măsură condiționat. Să începem cu tangente și cotangente în puteri mari. Din punct de vedere al metodelor folosite pentru rezolvarea tangentei și cotangentei sunt aproape aceleași, așa că voi vorbi mai mult despre tangentă, adică metoda demonstrată de rezolvare a integralei este valabilă și pentru cotangente.

În lecția de mai sus, ne-am uitat la substituție trigonometrică universală pentru rezolvarea unui anumit tip de integrale ale funcţiilor trigonometrice. Dezavantajul substituției trigonometrice universale este că aplicarea acesteia duce adesea la integrale greoaie cu calcule dificile. Și în unele cazuri, înlocuirea trigonometrică universală poate fi evitată!

Luați în considerare un alt exemplu canonic, integrala unității împărțită la sinus:

Exemplul 17

Aflați integrala nedefinită

Aici puteți folosi substituția trigonometrică universală și puteți obține răspunsul, dar există o modalitate mai rațională. Voi oferi o soluție completă cu comentarii pentru fiecare pas:

(1) Folosim formula trigonometrică pentru sinusul unui unghi dublu.
(2) Efectuăm o transformare artificială: La numitor împărțim și înmulțim cu .
(3) De către formula binecunoscuta la numitor transformăm fracția într-o tangentă.
(4) Aducem funcția sub semnul diferenţialului.
(5) Luăm integrala.

Pereche exemple simple pentru solutie independenta:

Exemplul 18

Aflați integrala nedefinită

Sugestie: Primul pas este utilizarea formulei de reducere și efectuați cu atenție acțiuni similare cu exemplul anterior.

Exemplul 19

Aflați integrala nedefinită

Ei bine, acesta este un exemplu foarte simplu.

Soluții complete și răspunsuri la sfârșitul lecției.

Cred că acum nimeni nu va avea probleme cu integralele:
etc.

Care este ideea din spatele metodei? Ideea este de a folosi transformări, formule trigonometrice pentru a organiza doar tangente și derivata tangentei în integrand. Adică vorbim despre înlocuirea: . În exemplele 17-19, am folosit de fapt această înlocuire, dar integralele erau atât de simple încât s-a făcut cu o acțiune echivalentă - aducerea funcției sub semnul diferențial.

Raționament similar, așa cum am menționat deja, poate fi efectuat pentru cotangentă.

Există, de asemenea, o condiție prealabilă formală pentru aplicarea înlocuirii de mai sus:

Suma puterilor cosinusului și sinusului este un număr întreg negativ PAR, de exemplu:

pentru o integrală, un număr întreg negativ PAR.

! Notă : dacă integrandul conține DOAR sinus sau DOAR cosinus, atunci integrala se ia par cu un grad impar negativ (cele mai simple cazuri sunt în Exemplele nr. 17, 18).

Luați în considerare câteva sarcini mai semnificative pentru această regulă:

Exemplul 20

Aflați integrala nedefinită

Suma gradelor de sinus și cosinus: 2 - 6 \u003d -4 - un număr întreg negativ PAR, ceea ce înseamnă că integrala poate fi redusă la tangente și derivata sa:

(1) Să transformăm numitorul.
(2) Conform formulei binecunoscute, obținem .
(3) Să transformăm numitorul.
(4) Folosim formula .
(5) Aducem funcția sub semnul diferențial.
(6) Efectuăm înlocuirea. Este posibil ca studenții mai experimentați să nu efectueze înlocuirea, dar totuși este mai bine să înlocuiți tangenta cu o singură literă - există mai puțin risc de confuzie.

Exemplul 21

Aflați integrala nedefinită

Acesta este un exemplu de do-it-yourself.

Stai, încep rundele de campionat =)

Adesea, în integrand există un „mezul”:

Exemplul 22

Aflați integrala nedefinită

Această integrală conține inițial o tangentă, care sugerează imediat un gând deja familiar:

Voi lăsa transformarea artificială chiar de la început și restul pașilor fără comentarii, deoarece totul a fost deja spus mai sus.

Pereche exemple creative pentru solutie independenta:

Exemplul 23

Aflați integrala nedefinită

Exemplul 24

Aflați integrala nedefinită

Da, în ele, bineînțeles, puteți scădea gradele sinusului, cosinusului, folosiți substituția trigonometrică universală, dar soluția va fi mult mai eficientă și mai scurtă dacă este trasată prin tangente. Soluție completă și răspunsuri la sfârșitul lecției

Vor exista și sarcini pentru o soluție independentă, la care puteți vedea răspunsurile.

Integrandul poate fi convertit dintr-un produs de funcții trigonometrice într-o sumă

Luați în considerare integralele în care integrandul este produsul dintre sinusuri și cosinusuri de gradul întâi al lui x înmulțit cu diferiți factori, adică integrale de forma

Profitând de binecunoscutul formule trigonometrice

(2)
(3)
(4)
se poate transforma fiecare dintre produsele în integrale de forma (31) într-o sumă algebrică și se poate integra prin formulele

(5)

(6)

Exemplul 1 A găsi

Soluţie. Conform formulei (2) la

Exemplul 2 A găsi integrală a funcției trigonometrice

Soluţie. Conform formulei (3) la

Exemplul 3 A găsi integrală a funcției trigonometrice

Soluţie. Conform formulei (4) la obținem următoarea transformare a integrandului:

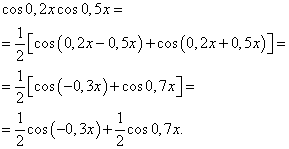
Aplicând formula (6), obținem

Integrală a produsului puterilor sinusului și cosinusului aceluiași argument

Să considerăm acum integralele funcțiilor care sunt produsul puterilor sinusului și cosinusului aceluiași argument, i.e.

(7)

În cazuri particulare, unul dintre indicatorii ( m sau n) poate fi zero.

La integrarea unor astfel de funcții, se folosește că puterea pară a cosinusului poate fi exprimată în termeni de sinus, iar diferența sinusului este egală cu cos x dx(sau o putere pară a sinusului poate fi exprimată în termeni de cosinus, iar diferența de cosinus este - sin x dx ) .

Trebuie distinse două cazuri: 1) cel puțin unul dintre indicatori mȘi n ciudat; 2) ambii indicatori sunt egali.

Să aibă loc primul caz, și anume exponentul n = 2k+ 1 - impar. Atunci, având în vedere că

Integrandul este prezentat în așa fel încât o parte a acestuia este o funcție doar a sinusului, iar cealaltă este diferențiala a sinusului. Acum cu schimbarea variabilei t= păcat X soluţia se reduce la integrarea polinomului în raport cu t. Dacă numai gradul m este impar, apoi procedați la fel, separând factorul sin X, exprimând restul integrandului în termeni de cos Xşi presupunând t= cos X. Această abordare poate fi folosită și atunci când integrarea puterilor parțiale ale sinusului și cosinusului , când cel puțin unul dintre indicatori este impar . Ideea este că câtul puterilor sinusului și cosinusului este un caz special al produsului lor : când funcția trigonometrică se află la numitorul integrandului, gradul acesteia este negativ. Dar există și cazuri de funcții trigonometrice parțiale, când gradele lor sunt doar pare. Despre ei - următorul paragraf.

Dacă ambii indicatori mȘi n sunt pare, folosind apoi formule trigonometrice

coborâți exponenții sinusului și cosinusului, după care se va obține o integrală de același tip ca mai sus. Prin urmare, integrarea ar trebui continuată în același mod. Dacă unul dintre indicatorii pare este negativ, adică se ia în considerare câtul puterilor pare ale sinusului și cosinusului, atunci această schemă nu este potrivită . Apoi se folosește o schimbare de variabilă, în funcție de modul în care poate fi transformat integrandul. Un astfel de caz va fi luat în considerare în secțiunea următoare.

Exemplul 4 A găsi integrală a funcției trigonometrice

Soluţie. Exponentul cosinusului este impar. Prin urmare, imaginați-vă

t= păcat X(apoi dt= cos X dx ). Apoi primim

Revenind la vechea variabilă, găsim în sfârșit

Exemplul 5 A găsi integrală a funcției trigonometrice

.

Soluţie. Exponentul cosinusului, ca în exemplul anterior, este impar, dar mai mult. Imagina

și faceți schimbarea variabilei t= păcat X(apoi dt= cos X dx ). Apoi primim

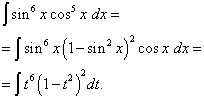
Să deschidem parantezele

si ia

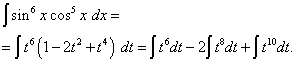
Revenind la vechea variabilă, obținem soluția

Exemplul 6 A găsi integrală a funcției trigonometrice

Soluţie. Exponenții sinusului și cosinusului sunt pari. Prin urmare, transformăm integrantul după cum urmează:

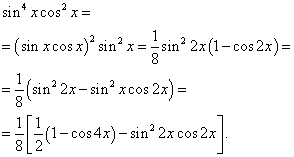
Apoi primim

În a doua integrală, facem o schimbare de variabilă, setare t= sin2 X. Apoi (1/2)dt= cos2 X dx . Prin urmare,

În sfârșit, obținem

Folosind metoda de înlocuire a variabilei

Metoda de înlocuire variabilă la integrarea funcțiilor trigonometrice, poate fi utilizat în cazurile în care în integrand este prezent doar un sinus sau numai un cosinus, produsul dintre sinus și cosinus, în care fie sinus, fie cosinus este de gradul I, tangent sau cotangent, de asemenea ca coeficientul puterilor pare ale sinusului si cosinusului unuia si aceluiasi argument. În acest caz, este posibil să se efectueze permutări nu numai păcat X = tși păcatul X = t, dar și tg X = t si ctg X = t .

Exemplul 8 A găsi integrală a funcției trigonometrice

.

Soluţie. Să schimbăm variabila: , apoi . Integrandul rezultat este ușor de integrat peste tabelul de integrale:

.

Exemplul 9 A găsi integrală a funcției trigonometrice

Soluţie. Să convertim tangenta la raportul dintre sinus și cosinus:

Să schimbăm variabila: , apoi . Integrandul rezultat este integral de tabel cu semnul minus:

.

Revenind la variabila inițială, obținem în sfârșit:

.

Exemplul 10 A găsi integrală a funcției trigonometrice

Soluţie. Să schimbăm variabila: , apoi .

Transformăm integrantul pentru a aplica identitatea trigonometrică :

Facem o schimbare de variabilă, fără a uita să punem semnul minus în fața integralei (vezi mai sus, ce este egal cu dt). În continuare, descompunem integrandul în factori și integrăm conform tabelului:

Revenind la variabila inițială, obținem în sfârșit:

.

Găsiți singur integrala funcției trigonometrice și apoi vedeți soluția

Substituție trigonometrică universală

Substituție trigonometrică universală poate fi folosit în cazurile în care integrantul nu se încadrează în cazurile discutate în paragrafele precedente. Practic atunci când sinusul sau cosinusul (sau ambele) se află în numitorul unei fracții. Se dovedește că sinusul și cosinusul pot fi înlocuite cu o altă expresie care conține tangenta jumătății unghiului inițial astfel:

Dar rețineți că substituția trigonometrică universală implică adesea transformări algebrice destul de complexe, deci este cel mai bine utilizată atunci când nicio altă metodă nu funcționează. Să ne uităm la exemple când, împreună cu substituția trigonometrică universală, se utilizează scăderea sub semnul diferențialei și metoda coeficienților nedeterminați.

Exemplul 12. A găsi integrală a funcției trigonometrice

.

Soluţie. Soluţie. Să folosim substituție trigonometrică universală. Apoi
.

Înmulțim fracțiile din numărător și numitor cu , și scoatem doi și îl punem în fața semnului integral. Apoi

Pentru a integra funcții raționale de forma R(sin x, cos x), se folosește o substituție, care se numește substituție trigonometrică universală. Apoi . Substituția trigonometrică universală duce adesea la calcule mari. Prin urmare, ori de câte ori este posibil, utilizați următoarele înlocuiri.

Integrarea funcţiilor dependente raţional de funcţiile trigonometrice

1. Integrale de forma ∫ sin n xdx , ∫ cos n xdx , n>0
a) Dacă n este impar, atunci o putere a lui sinx (sau cosx) ar trebui să fie plasată sub semnul diferenţialului, iar din puterea pară rămasă trebuie să treceţi la funcţia opusă.
b) Dacă n este par, atunci folosim formulele de reducere
2. Integrale de forma ∫ tg n xdx , ∫ ctg n xdx , unde n este un număr întreg.
Trebuie folosite formule

3. Integrale de forma ∫ sin n x cos m x dx
a) Fie m și n de paritate diferită. Aplicam substitutia t=sin x daca n este impar sau t=cos x daca m este impar.
b) Dacă m și n sunt pare, atunci folosim formulele de reducere
2sin 2 x=1-cos2x , 2cos 2 x=1+cos2x .
4. Integrale ale formei
Dacă numerele m și n au aceeași paritate, atunci folosim substituția t=tg x . Este adesea convenabil să se aplice tehnica unității trigonometrice.
5. ∫ sin(nx) cos(mx)dx , ∫ cos(mx) cos(nx)dx , ∫ sin(mx) sin(nx)dx

Să folosim formulele pentru conversia produsului funcțiilor trigonometrice în suma lor:

• sin α cos β = ½(sin(α+β)+sin(α-β))
• cos α cos β = ½(cos(α+β)+cos(α-β))
• sin α sin β = ½(cos(α-β)-cos(α+β))

Exemple
1. Calculați integrala ∫ cos 4 x sin 3 xdx .
Facem substituția cos(x)=t . Atunci ∫ cos 4 x sin 3 xdx =
2. Calculați integrala.
Făcând substituția sin x=t , obținem

3. Aflați integrala.
Facem înlocuirea tg(x)=t . Înlocuind, obținem

Integrarea expresiilor de forma R(sinx, cosx)

Exemplul #1. Calculați integralele:

Soluţie.
a) Integrarea expresiilor de forma R(sinx, cosx) , unde R este o funcție rațională a sin x și cos x , sunt convertite în integrale ale funcțiilor raționale folosind substituția trigonometrică universală tg(x/2) = t .
Atunci noi avem

Substituția trigonometrică universală face posibilă trecerea de la o integrală de forma ∫ R(sinx, cosx) dx la o integrală a unei funcții rațional-fracționale, dar o astfel de înlocuire duce adesea la expresii greoaie. În anumite condiții, substituțiile mai simple se dovedesc a fi eficiente:

• Dacă egalitatea R(-sin x, cos x) = -R(sin x, cos x)dx este adevărată, atunci se aplică substituția cos x = t.
• Dacă R(sin x, -cos x) = -R(sin x, cos x)dx este adevărată, atunci substituția sin x = t .
• Dacă R(-sin x, -cos x) = R(sin x, cos x)dx este adevărată, atunci substituția este tgx = t sau ctg x = t .

În acest caz, pentru a găsi integrala
aplicăm substituția trigonometrică universală tg(x/2) = t .
Apoi raspunde: