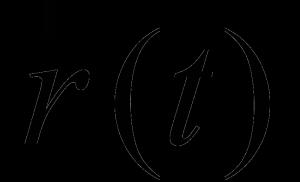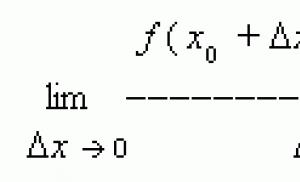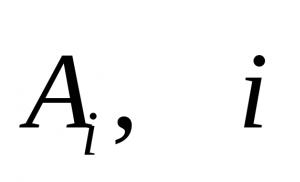Definirea unei integrale curbilinii pe lungimea unui arc. Calculați integrala curbilinie de primul fel peste arcul L. Curba este dată în formă parametrică

Integrala curbilinie de al 2-lea fel se calculează la fel ca integrala curbilinie de primul fel prin reducere la una definită. Pentru a face acest lucru, toate variabilele sub semnul integral sunt exprimate în termenii unei singure variabile, folosind ecuația dreptei de-a lungul căreia se realizează integrarea.

a) Dacă linia AB dat de sistemul de ecuaţii atunci

(10.3)

Pentru cazul plan, când curba este dată de ecuație integrala curbilinie se calculează prin formula: . (10.4)

Dacă linia AB dat de ecuaţii parametrice atunci

(10.5)

Pentru carcasa plată, dacă linia AB dat de ecuaţii parametrice , integrala curbilinie se calculează cu formula:

, (10.6)

unde - valorile parametrilor t, corespunzătoare punctelor de început și de sfârșit ale traseului de integrare.

Dacă linia AB netedă pe bucăți, atunci ar trebui să se folosească proprietatea de aditivitate a integralei curbilinii, divizare AB pe curbe netede.

Exemplul 10.1 Se calculează integrala curbilinie de-a lungul unui contur format dintr-o parte dintr-o curbă dintr-un punct inainte de și arcurile unei elipse din punct de vedere inainte de .

Deoarece conturul constă din două părți, folosim proprietatea de aditivitate a integralei curbilinii: . Reducem ambele integrale la unele definite. O parte a conturului este dată de ecuația față de variabilă . Să folosim formula (10.4 ), în care schimbăm rolurile variabilelor. Acestea.

. După calcul, obținem .

Pentru a calcula integrala conturului soare să trecem la forma parametrică de scriere a ecuației elipsei și să folosim formula (10.6).

Acordați atenție limitelor integrării. punct corespunde valorii și punctului corespunde Răspuns:
.

Exemplul 10.2. Calculați de-a lungul unui segment de dreaptă AB, Unde A(1,2,3), B(2,5,8).

Soluţie. Este dată o integrală curbilinie de al 2-lea fel. Pentru a-l calcula, trebuie să îl convertiți într-unul anume. Să facem ecuații ale unei linii drepte. Vectorul său de direcție are coordonate .

Ecuații canonice ale dreptei AB: .

Ecuații parametrice ale acestei linii drepte: ,

La
.

Să folosim formula (10.5) :

După ce calculăm integrala, obținem răspunsul: .

5. Lucrul unei forțe atunci când se deplasează un punct material al unei unități de masă dintr-un punct în altul de-a lungul unei curbe .

Lăsați în fiecare punct al curbei netede pe bucăți se da un vector care are functii-coordonate continue: . Să împărțim această curbă în părți mici pe puncte astfel încât în ​​punctele fiecărei părți valoarea functiei
ar putea fi considerat permanent și piesa în sine ar putea fi luat ca un segment de linie dreaptă (vezi Fig. 10.1). Apoi . Produsul scalar al unei forțe constante, al cărei rol este jucat de un vector , pe un vector de deplasare rectiliniu este numeric egal cu munca pe care o face forța atunci când se deplasează un punct material de-a lungul . Să facem o sumă integrală . În limită, cu o creștere nelimitată a numărului de partiții, obținem o integrală curbilinie de felul 2

. (10.7) Astfel, sensul fizic al integralei curbilinii de felul al 2-lea - este o muncă făcută cu forța la mutarea unui punct material din A La ÎN de-a lungul conturului L.

Exemplul 10.3. Calculați munca efectuată de vector când se deplasează un punct de-a lungul părții curbei Viviani, dat ca intersecție a emisferei si cilindru mergând în sens invers acelor de ceasornic când este privit din partea pozitivă a axei BOU.

Soluţie. Să construim o curbă dată ca o linie de intersecție a două suprafețe (vezi Fig. 10.3).

.

Pentru a reduce integrantul la o singură variabilă, să trecem la un sistem de coordonate cilindric: .

Deoarece punctul se deplasează de-a lungul curbei , atunci este convenabil să alegeți ca parametru variabila , care se modifică de-a lungul conturului astfel încât . Apoi obținem următoarele ecuații parametrice pentru această curbă:

.Unde
.

Inlocuim expresiile obtinute in formula de calcul a circulatiei:

(- semnul + indică faptul că mișcarea punctului de-a lungul conturului este în sens invers acelor de ceasornic)

Calculăm integrala și obținem răspunsul: .

Lecția 11.

Formula lui Green pentru un domeniu simplu conectat. Independența integralei curbilinii față de calea integrării. formula Newton-Leibniz. Găsirea unei funcții prin diferența sa totală folosind o integrală curbilinie (cazuri plane și spațiale).

OL-1 cap.5, OL-2 cap.3, OL-4 cap.3 § 10, p. 10.3, 10.4.

Practică : OL-6 nr. 2318 (a, b, e), 2319 (a, c), 2322 (a, d), 2327, 2329 sau OL-5 nr. 10.79, 82, 133, 135, 139.

Construirea casei pentru lecția 11: OL-6 nr. 2318 (c, d), 2319 (c, d), 2322 (b, c), 2328, 2330 sau OL-5 nr. 10.80, 134, 136, 140

Formula lui Green.

Lasă în avion dat un domeniu simplu conectat delimitat de un contur închis neted pe bucăți. (Un domeniu se numește simplu conectat dacă orice contur închis din el poate fi contractat la un punct din acest domeniu).

Teorema. Dacă funcţiile și derivatele lor parțiale G, Acea

Figura 11.1

- Formula lui Green . (11.1)

Indică direcția pozitivă de traversare (în sens invers acelor de ceasornic).

Exemplul 11.1. Folosind formula lui Green, calculăm integrala de-a lungul unui contur format din segmente OA, OBși un arc de cerc mai mare puncte de legătură AȘi b, Dacă , , .

Soluţie. Să construim un contur (vezi fig. 11.2). Să calculăm derivatele necesare.

Figura 11.2

, ; , . Funcțiile și derivatele lor sunt continue într-o regiune închisă delimitată de un contur dat. Conform formulei lui Green, această integrală este .

După înlocuirea derivatelor calculate, obținem

. Calculăm integrala dublă trecând la coordonatele polare:
.

Să verificăm răspunsul calculând integrala direct peste contur ca o integrală curbilinie de al 2-lea fel.
.

Răspuns:
.

2. Independenta Integralei Curbilinii de Calea de Integrare.

Lăsa Și - puncte arbitrare ale unei arii simplu conexate pl. . Integrale curbilinii calculate din diferite curbe care leagă aceste puncte au în general valori diferite. Dar, în anumite condiții, toate aceste valori pot fi aceleași. Apoi integrala nu depinde de forma traseului, ci depinde doar de punctele de început și de sfârșit.

Următoarele teoreme sunt valabile.

Teorema 1. Pentru ca integrala
nu depinde de forma traseului care leagă punctele și , este necesar și suficient ca această integrală peste orice contur închis să fie egală cu zero.

Teorema 2.. Pentru ca integrala
este egal cu zero de-a lungul oricărui contur închis, este necesar și suficient ca funcțiile și derivatele lor parțiale au fost continue într-o regiune închisă Gși astfel încât starea ( 11.2)

Astfel, dacă sunt îndeplinite condițiile de independență a integralei față de forma căii (11.2) , atunci este suficient să specificați doar punctele de început și de sfârșit: (11.3)

Teorema 3. Dacă condiția este îndeplinită într-un domeniu simplu conectat, atunci există o funcție astfel încât . (11.4)

Această formulă se numește formulă Newton-Leibniz pentru integrala curbilinie.

Cometariu. Amintiți-vă că egalitatea este o condiție necesară și suficientă pentru expresie
.

Atunci din teoremele formulate mai sus rezultă că dacă funcţiile și derivatele lor parțiale continuă într-o regiune închisă G, în care sunt date puncte Și , și apoi

a) există o funcție , astfel încât ,

nu depinde de forma căii, ,

c) formula este valabilă Newton-Leibniz .

Exemplul 11.2. Să ne asigurăm că integrala
nu depinde de forma căii și calculează-l.

Soluţie. .

Figura 11.3

Să verificăm îndeplinirea condiției (11.2) .
. După cum puteți vedea, condiția este îndeplinită. Valoarea integralei nu depinde de calea de integrare. Alegem calea integrării. Cel mai

o modalitate simplă de a calcula este o linie întreruptă DIA care leagă punctele de început și de sfârșit ale căii. (Vezi fig. 11.3)

Apoi .

3. Găsirea unei funcții prin diferența sa totală.

Cu ajutorul unei integrale curbilinii, care nu depinde de forma traseului, se poate găsi funcția cunoscându-i diferența totală. Această problemă este rezolvată în felul următor.

Dacă funcţiile și derivatele lor parțiale continuă într-o regiune închisă Gși , atunci expresia este diferența totală a unei funcții . În plus, integrala
, în primul rând, nu depinde de forma căii și, în al doilea rând, poate fi calculat folosind formula Newton-Leibniz.

Calcula
doua feluri.

Figura 11.4

a) Alegeți un punct din regiune cu coordonate specifice și un punct cu coordonate arbitrare. Să calculăm integrala curbilinie de-a lungul unei linii întrerupte constând din două segmente de drepte care leagă aceste puncte, unul dintre segmente fiind paralel cu axa și celălalt cu axa. Apoi . (Vezi fig. 11.4)

Ecuația .

Ecuația .

Obținem: După ce am calculat ambele integrale, obținem o funcție în răspuns.

b) Acum putem calcula aceeași integrală folosind formula Newton-Leibniz.

Acum să comparăm două rezultate ale calculării aceleiași integrale. Partea funcțională a răspunsului de la paragraful a) este funcția dorită , iar partea numerică - valoarea sa în punct .

Exemplul 11.3. Să ne asigurăm că expresia
este diferența totală a unei funcții si hai sa-l gasim. Să verificăm rezultatele calculului exemplului 11.2 folosind formula Newton-Leibniz.

Soluţie. Funcție Condiție de existență (11.2) a fost verificat în exemplul anterior. Să găsim această funcție, pentru care vom folosi Figura 11.4, și vom lua pentru punct . Compuneți și calculați integrala peste linia întreruptă DIA, Unde :

După cum sa menționat mai sus, partea funcțională a expresiei rezultate este funcția dorită
.

Să verificăm rezultatul calculelor din exemplul 11.2 folosind formula Newton-Leibniz:

Rezultatele s-au potrivit.

Cometariu. Toate afirmațiile luate în considerare sunt valabile și pentru cazul spațial, dar cu un număr mare de condiții.

Fie ca o curbă netedă pe bucăți să aparțină unui domeniu în spațiu . Atunci, dacă funcțiile și derivatele lor parțiale sunt continue într-o regiune închisă în care sunt date puncte si si
(11.5 ), Acea

a) expresia este diferenta totala a unei functii ,

b) o integrală curbilinie a diferenţialului total al unei funcţii nu depinde de forma căii și,

c) formula este valabilă Newton-Leibniz .(11.6 )

Exemplul 11.4. Să ne asigurăm că expresia este diferența totală a unei funcții si hai sa-l gasim.

Soluţie. Pentru a răspunde la întrebarea dacă o expresie dată este diferența totală a unei funcții , calculați derivatele parțiale ale funcțiilor , , . (Cm. (11.5) ) ; ; ; ; ; .

Aceste funcții sunt continue împreună cu derivatele lor parțiale în orice punct din spațiu.

Vedem că condițiile necesare și suficiente pentru existența : , , , h.t.d.

Pentru a calcula funcția folosim faptul că integrala dreaptă nu depinde de calea de integrare și poate fi calculată folosind formula Newton-Leibniz. Lasă punctul - începutul căii și un punct - Sfarsit de drum . Calculăm integrala

de-a lungul unui contur format din segmente de linie paralele cu axele de coordonate. (vezi fig. 11.5).

.

Figura 11.5

Ecuații ale părților de contur: , ,
.

Apoi

, X fixat aici, deci ,

S-a rezolvat aici y, De aceea .

Ca rezultat, obținem:

Acum putem calcula aceeași integrală folosind formula Newton-Leibniz.

Să comparăm rezultatele: .

Din egalitatea rezultată rezultă că , și

Lecția 12.

Integrală de suprafață de primul fel: definiție, proprietăți de bază. Reguli pentru calcularea integralei de suprafață de primul fel folosind o integrală dublă. Aplicații ale integralei de suprafață de primul fel: aria suprafeței, masa suprafeței materialului, momentele statice despre planuri de coordonate, momentele de inerție și coordonatele centrului de greutate. OL-1 cap.6, OL 2 cap.3, OL-4 § 11.

Practică: OL-6 nr. 2347, 2352, 2353 sau OL-5 nr. 10.62, 65, 67.

Tema pentru lecția 12:

OL-6 nr. 2348, 2354 sau OL-5 nr. 10.63, 64, 68.

Pentru cazul în care aria de integrare este un segment al unei curbe situate într-un plan. Notația generală a integralei curbilinie este următoarea:

Unde f(X, y) este o funcție a două variabile și L- curba, pe segment ABîn care are loc integrarea. Dacă integrandul este egal cu unu, atunci integrala curbilinie este egală cu lungimea arcului AB .

Ca întotdeauna în calculul integral, integrala curbilinie este înțeleasă ca limita sumelor integrale ale unor părți foarte mici ale ceva foarte mare. Ce se rezumă în cazul integralelor curbilinii?

Să fie un segment în plan AB vreo curbă L, și funcția a două variabile f(X, y) definite în punctele curbei L. Să realizăm următorul algoritm cu acest segment al curbei.

1. Curba împărțită AB pe partea cu puncte (figurile de mai jos).
2. În fiecare parte, alegeți liber un punct M.
3. Găsiți valoarea funcției în punctele selectate.
4. Înmulțiți valorile funcției cu
   • lungimea pieselor in caz integrală curbilinie de primul fel ;
   • proiecții ale pieselor pe axa de coordonate în caz integrală curbilinie de al doilea fel .
5. Găsiți suma tuturor produselor.
6. Aflați limita sumei integrale găsite cu condiția ca lungimea celei mai lungi părți a curbei să tinde spre zero.

Dacă această limită există, atunci aceasta limita sumei integrale și se numește integrală curbilinie a funcției f(X, y) de-a lungul curbei AB .

primul fel

Caz integral curbiliniu
al doilea fel

Să introducem următoarea notație.

Meu ( ζ eu ; η i)- un punct cu coordonatele selectate pe fiecare secțiune.

feu ( ζ eu ; η i)- valoarea funcției f(X, y) în punctul ales.

Δ si- lungimea unei părți dintr-un segment al curbei (în cazul unei integrale curbilinii de primul fel).

Δ Xi- proiecția unei părți a segmentului de curbă pe axă Bou(în cazul unei integrale curbilinii de al doilea fel).

d= maxΔ s i este lungimea celei mai lungi părți a segmentului de curbă.

Integrale curbilinii de primul fel

Pe baza celor de mai sus despre limita sumelor integrale, integrala curbilinie de primul fel se scrie astfel:

.

Integrala curbilinie de primul fel are toate proprietăţile care integrala definita. Cu toate acestea, există o diferență importantă. Pentru o integrală definită, atunci când limitele integrării sunt schimbate, semnul se schimbă la opus:

În cazul unei integrale curbilinii de primul fel, nu contează care dintre punctele curbei AB (A sau B) luați în considerare începutul segmentului și care sfârșit, adică

.

Integrale curbilinii de al doilea fel

Pe baza celor spuse despre limita sumelor integrale, integrala curbilinie de al doilea fel se scrie astfel:

.

În cazul unei integrale curbilinii de al doilea fel, când începutul și sfârșitul unui segment al curbei sunt inversate, semnul integralei se modifică:

.

La compilarea sumei integrale a unei integrale curbilinii de al doilea fel, valorile funcției feu ( ζ eu ; η i) poate fi înmulțit și cu proiecția părților segmentului de curbă pe axă Oi. Apoi obținem integrala

.

În practică, se utilizează de obicei unirea integralelor curbilinie de al doilea fel, adică două funcții f = P(X, y) Și f = Q(X, y) și integrale

,

și suma acestor integrale

numit integrală curbilinie generală de al doilea fel .

Calculul integralelor curbilinie de primul fel

Calculul integralelor curbilinie de primul fel se reduce la calculul integralelor definite. Să luăm în considerare două cazuri.

Să fie dată o curbă pe plan y = y(X) și un segment de curbă AB corespunde cu schimbarea variabilei X din A inainte de b. Apoi în punctele curbei integrandul f(X, y) = f(X, y(X)) ("y" trebuie exprimat prin "x") și diferența de arc iar integrala curbilinie poate fi calculată prin formula

.

Dacă integrala este mai ușor de integrat peste y, apoi din ecuația curbei trebuie exprimat X = X(y) ("x" prin "y"), unde și integrala se calculează prin formula

.

Exemplul 1

Unde AB- segment de linie între puncte A(1; −1) și B(2; 1) .

Soluţie. Compuneți ecuația unei linii drepte AB, folosind formula (ecuația unei drepte care trece prin două puncte date A(X1 ; y 1 ) Și B(X2 ; y 2 ) ):

Din ecuația unei drepte exprimăm y prin X :

Atunci și acum putem calcula integrala, deoarece ne rămâne doar „x”:

Să fie dată o curbă în spațiu

Apoi, în punctele curbei, funcția trebuie exprimată în termeni de parametru t() și diferența de arc , deci integrala curbilinie poate fi calculată prin formula

În mod similar, dacă este dată o curbă pe plan

,

atunci integrala curbilinie se calculează prin formula

.

Exemplul 2 Calculați integrala curbilinie

Unde L- parte a liniei cercului

situat în primul octant.

Soluţie. Această curbă este un sfert din linia cercului, situată în plan z= 3 . Corespunde cu valorile parametrilor. Deoarece

apoi diferenţialul arcului

Să exprimăm integrandul în termeni de parametru t :

Acum că avem totul exprimat printr-un parametru t, putem reduce calculul acestei integrale curbilinie la o integrală definită:

Calculul integralelor curbilinii de al doilea fel

La fel ca în cazul integralelor curbilinii de primul fel, calculul integralelor de al doilea fel se reduce la calculul integralelor definite.

Curba este dată în coordonate dreptunghiulare carteziene

Fie o curbă pe un plan dată de ecuația funcției „y”, exprimată prin „x”: y = y(X) iar arcul curbei AB corespunde schimbarea X din A inainte de b. Apoi substituim expresia „y” prin „x” în integrand și determinăm diferența acestei expresii „y” față de „x”: . Acum, când totul este exprimat prin „x”, integrala curbilinie de al doilea fel este calculată ca o integrală definită:

În mod similar, o integrală curbilinie de al doilea fel este calculată atunci când curba este dată de ecuația funcției „x”, exprimată prin „y”: X = X(y) , . În acest caz, formula de calcul a integralei este următoarea:

Exemplul 3 Calculați integrala curbilinie

, Dacă

A) L- segment de linie dreaptă OA, Unde DESPRE(0; 0) , A(1; −1) ;

b) L- arc de parabolă y = X² de la DESPRE(0; 0) la A(1; −1) .

a) Calculați integrala curbilinie pe un segment de dreaptă (albastru în figură). Să scriem ecuația unei linii drepte și să exprimăm „Y” prin „X”:

.

Primim dy = dx. Rezolvăm această integrală curbilinie:

b) dacă L- arc de parabolă y = X², primim dy = 2xdx. Calculăm integrala:

În exemplul tocmai rezolvat, am obținut același rezultat în două cazuri. Și aceasta nu este o coincidență, ci rezultatul unui model, deoarece această integrală satisface condițiile următoarei teoreme.

Teorema. Dacă funcţiile P(X,y) , Q(X,y) şi derivatele lor parţiale , - continuu în regiune D funcții și în punctele acestei regiuni, derivatele parțiale sunt egale, atunci integrala curbilinie nu depinde de calea de integrare de-a lungul liniei L situat în regiune D .

Curba este dată sub formă parametrică

Să fie dată o curbă în spațiu

.

iar în integranţi substituim

expresii ale acestor funcţii printr-un parametru t. Obținem formula pentru calcularea integralei curbilinii:

Exemplul 4 Calculați integrala curbilinie

,

Dacă L- parte a unei elipse

îndeplinirea condiției y ≥ 0 .

Soluţie. Această curbă este partea elipsei care se află în plan z= 2 . Ea corespunde valorii parametrului.

putem reprezenta integrala curbilinie ca o integrală definită și o putem calcula:

Având în vedere o integrală curbilinie și L- o linie închisă, atunci o astfel de integrală se numește integrală peste un contur închis și este mai ușor să o calculezi folosind Formula lui Green .

Mai multe exemple de calcul a integralelor curbilinie

Exemplul 5 Calculați integrala curbilinie

Unde L- un segment de dreaptă între punctele sale de intersecție cu axele de coordonate.

Soluţie. Să determinăm punctele de intersecție ale dreptei cu axele de coordonate. Înlocuirea dreptei în ecuație y= 0 , obținem , . Înlocuind X= 0 , obținem , . Astfel, punctul de intersecție cu axa Bou - A(2; 0) , cu axa Oi - B(0; −3) .

Din ecuația unei drepte exprimăm y :

.

, .

Acum putem reprezenta integrala curbilinie ca o integrală definită și începem să o calculăm:

În integrand, selectăm factorul , îl scoatem din semnul integral. În integrantul rezultat, aplicăm aducând sub semnul diferenţialuluiși în sfârșit obținem.

Definiție: Lăsați în fiecare punct al unei curbe netede L=AB in avion Oxy dată o funcţie continuă a două variabile f(x,y). Să împărțim curba în mod arbitrar L pe n piese puncte A \u003d M 0, M 1, M 2, ... M n \u003d B. Apoi, pe fiecare dintre părțile obținute \(\bar((M)_(i-1)(M)_(i))\) alegeți orice punct \(\bar((M)_(i))\left (\ bar((x)_(i)),\bar((y)_(i))\right)\) și faceți suma $$(S)_(n)=\sum_(i=1) ^(n )f\left(\bar((x)_(i)),\bar((y)_(i))\right)\Delta (l)_(i)$$ unde \(\Delta (l) _(i)=(M)_(i-1)(M)_(i)\) - arc de arc \(\bar((M)_(i-1)(M)_(i ))\) . Se numește suma primită suma integrală de primul fel pentru funcție f(x,y) , dat pe curba L.

Notează prin d cea mai mare dintre lungimile arcului \(\bar((M)_(i-1)(M)_(i))\) (astfel d = \(max_(i)\Delta(l)_(i)\) )). Daca pentru d? 0 există o limită a sumelor integrale S n (care nu depind de metoda de împărțire a curbei L în părți și de alegerea punctelor \(\bar((M)_(i))\)), atunci această limită se numește integrală curbilinie de ordinul întâi din functie f(x,y) de-a lungul curbei L și notat cu $$\int_(L)f(x,y)dl$$

Se poate arăta că dacă funcţia f(x,y) este continuă, atunci integrala curbilinie \(\int_(L)f(x,y)dl\) există.

Proprietățile unei integrale curbilinii de primul fel

Integrala curbilinie de primul fel are proprietăți similare cu proprietățile corespunzătoare ale integralei definite:

• aditivitate,
• liniaritate,
• evaluarea modulului,
• teorema valorii medii.

Cu toate acestea, există o diferență: $$\int_(AB)f(x,y)dl=\int_(BA)f(x,y)dl$$ adică. integrala curbilinie de primul fel nu depinde de sensul de integrare.

Calculul integralelor curbilinie de primul fel

Calculul unei integrale curbilinii de primul fel se reduce la calculul unei integrale definite. Și anume:

1. Dacă curba L este dată de o funcție diferențiabilă continuu y=y(x), x \(\in \) , atunci $$(\int\limits_L (f\left((x,y) \right)dl) ) = (\int \limits_a^b (f\left((x,y\left(x \right)) \right)\sqrt (1 + ((\left((y"\left(x \right))) \ dreapta))^ 2)) dx) ;)$$ în timp ce expresia \(dl=\sqrt((1 + ((\left((y"\left(x \right))) \right))^2)) ) dx \) se numește diferența de lungime a arcului.
2. Dacă curba L este dată parametric, i.e. în forma x=x(t), y=y(t), unde x(t), y(t) sunt funcții diferențiabile continuu pe un anumit segment \(\left [ \alpha ,\beta \right ]\), apoi $$ (\int\limits_L (f\left((x,y) \right)dl) ) = (\int\limits_\alpha ^\beta (f\left ((x\left(t \right),), y \left(t \right)) \right)\sqrt (((\left((x"\left(t \right)) \right))^2) + ((\left((y"\left() t \right)) \right))^2)) dt)) $$ Această egalitate se extinde la cazul unei curbe spațiale L definită parametric: x=x(t), y=y(t), z=z( t), \(t\in \left [ \alpha ,\beta \right ]\). În acest caz, dacă f(x,y,z) este o funcție continuă de-a lungul curbei L, atunci $$ (\int\limits_L (f\left((x,y,z) \right)dl) ) = ( \int \limits_\alpha ^\beta (f\left [ (x\left(t \right),y\left(t \right),z\left(t \right)) \right ]\sqrt ((( \left ((x"\left(t \right)) \right))^2) + ((\left((y"\left(t \right)) \right))^2) + ((\left) (( z"\stânga(t\dreapta)) \dreapta))^2)) dt)) $$
3. Dacă curba plană L este dată de ecuația polară r=r(\(\varphi \)), \(\varphi \in\left [ \alpha ,\beta \right ] \), atunci $$ (\int\ limits_L (f\ left((x,y) \right)dl) ) = (\int\limits_\alpha ^\beta (f\left((r\cos \varphi ,r\sin \varphi ) \right)\ sqrt ((r ^2) + (((r)")^2)) d\varphi)) $$

Integrale curbilinii de primul fel - exemple

Exemplul 1

Calculați o integrală curbilinie de primul fel

$$ \int_(L)\frac(x)(y)dl $$ unde L este arcul parabolei y 2 =2x între punctele (2,2) și (8,4).

Soluție: Găsiți diferența de arc dl pentru curba \(y=\sqrt(2x)\). Avem:

\((y)"=\frac(1)(\sqrt(2x)) \) $$ dl=\sqrt(1+\left ((y)" \right)^(2)) dx= \sqrt( 1+\left (\frac(1)(\sqrt(2x)) \right)^(2)) dx = \sqrt(1+ \frac(1)(2x)) dx $$ Prin urmare, această integrală este: $ $\int_(L)\frac(x)(y)dl=\int_(2)^(8)\frac(x)(\sqrt(2x))\sqrt(1+\frac(1)(2x) ) )dx= \int_(2)^(8)\frac(x\sqrt(1+2x))(2x)dx= $$ $$ \frac(1)(2)\int_(2)^(8 ) \sqrt(1+2x)dx = \frac(1)(2).\frac(1)(3)\left (1+2x \right)^(\frac(3)(2))|_( 2 )^(8)= \frac(1)(6)(17\sqrt(17)-5\sqrt(5)) $$

Exemplul 2

Calculați integrala curbilinie de primul fel \(\int_(L)\sqrt(x^2+y^2)dl \), unde L este cercul x 2 +y 2 =ax (a>0).

Rezolvare: Să introducem coordonatele polare: \(x = r\cos \varphi \), \(y=r\sin \varphi \). Atunci, deoarece x 2 +y 2 =r 2 , ecuația cercului are forma: \(r^(2)=arcos\varphi \), adică \(r=acos\varphi \), iar diferența de arc $$ dl = \ sqrt(r^2+(2)"^2)d\varphi = $$ $$ =\sqrt(a^2cos^2\varphi=a^2sin^2\varphi )d\varphi=ad\varphi $$ .

Astfel \(\varphi\in \left [- \frac(\pi )(2) ,\frac(\pi )(2) \right ] \). Prin urmare, $$ \int_(L)\sqrt(x^2+y^2)dl=a\int_(-\frac(\pi )(2))^(\frac(\pi )(2))acos \varphi d\varphi =2a^2 $$