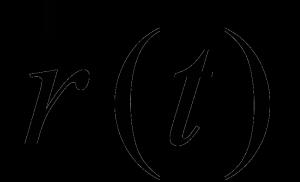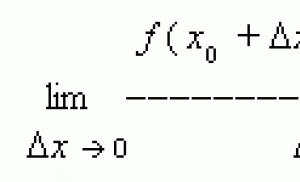Calcule pentru funcții de argument vectorial. Specificarea unei funcții folosind un vector adevăr. Specificarea utilizării unui arbore binar complet

Descărcați din Depositfiles

GEOMETRIE DIFERENȚIALĂ

eu. FUNCȚIA VECTORALĂ A ARGUMENTULUI SCALAR

Funcția vectorială (definiția 1.1), metode de specificare a acesteia.

Vector de rază și hodograf, specificație parametrică odograf.

Derivată a unei funcții vectoriale (Definiția 1.6).

Semnificația geometrică a derivatei unei funcții vectoriale.

Reguli de diferențiere a funcțiilor vectoriale.

1.1. DEFINIȚIA FUNCȚIEI VECTORALE

Definiție 1.1Dacă fiecare valoare a argumentului scalarvector potrivit
spatiu tridimensional R3 , atunci ei spun că o funcție vectorială (sau funcție vectorială) a unui argument scalar este dată pe mulțimea Xt .

Dacă în spațiu R3 este specificat un sistem de coordonate cartezieneDESPRE xyz , atunci sarcina este un vector - funcție
,
este echivalent cu specificarea a trei funcții scalareX( t ), y ( t ), z ( t ) – coordonate vectoriale:

= { X ( t ), y ( t ), z ( t )} (1.1)

sau , (1.2)

Unde
— vectori unitari de coordonate.

1.2. LINIA SPAȚIALĂ CA O HODOGRAFĂ A VECTORULUI DE RAZĂ

Definiție 1.2 Dacă începutul tuturor vectorilor este ,plasate la origine, se numesc vectori cu raza.

Definiție 1.3 Linia care este locul geometric al capetelor vectorilor cu rază , , se numește hodograful funcției vectoriale, iar începutul lor comun este polul hodograf.

Dacă parametrul t este timpul și este vectorul rază al punctului în mișcare, atunci hodograful funcției este traiectoria punctului în mișcare.

Ecuația hodografă poate fi scrisă sub formă vectorială (1.2) sau sub formă parametrică:

(1.3)

În special, dacă funcția vectorialăcu o schimbare a argumentului, se schimbă doar modulul său, dar direcția nu se schimbă (), atunci hodograful unei astfel de funcție vectorială va fi o rază rectilinie care emană de la origine; dacă doar direcția vectorului se schimbă, dar mărimea acestuia rămâne neschimbată (
), atunci hodograful funcției vectoriale va fi o curbă situată pe o sferă cu un centru la pol și o rază egală cu modulul constant al vectorului.

Poza 1.

1.3. LIMITĂ, CONTINUITATE ȘI DERIVAT AL VECTOR-FUNȚII

Definiția 1. 4 Vector se numește limita funcției vectorialela
, Dacă

. (1.4)

Definiția 1.5 Funcția vectorială este numită continuu la un punctt 0, dacă are o limită în acest punct egală cu valoarea funcției vectoriale în acest punct:

. (1.5)

Definiția 1.6Derivată a unei funcții vectoriale la punct t se numește limita raportului dintre incrementul unei funcții vectoriale și incrementul argumentului
la
:

(1.6)

1.4. SEMNIFICAȚIA GEOMETRICĂ ȘI MECANICĂ A PRIMULUI DERIVAT AL FUNCȚIEI VECTORALE

Sensul geometric al primei derivate a funcției vectoriale a argumentului scalar este că această derivată este un vector nou direcționat tangențial la hodograf:
. Să o arătăm.

Figura 2

Vom presupune că hodograful funcției vectoriale luate în considerare este o linie continuă care are o tangentă în orice punct.

Să dăm argumentul t increment, apoi geometric raportul
este un vector
, culcat pe secanta MM’. Când acest vector se rotește și se transformă într-un vector
, culcat pe tangentă și îndreptat spre creșteret . Deci vectorul

(1.7)

va fi un vector tangent unitar orientat în direcția creșterii parametruluit .

Prin urmare, vectorul
poate fi luat ca un vector de direcție tangent la curba în punctul ), (sau
) și scrieți ecuația tangentei sub forma:

(1.8)

Dacă t – timp și — vectorul rază al unui punct
, deplasându-se în spațiul tridimensional, apoi aproximativrelația se numește viteza medie a unui punct de pe segment [t; t+t].

Sensul mecanicprima derivată a funcției vectoriale este că această derivată reprezintă viteza punctului M în momentul de fațăt :

Reguli de diferențiere a funcțiilor vectoriale

Să demonstrăm regula 1 folosind regulile pentru scăderea vectorilor și împărțirea unui vector la un număr:

Dovada regulilor rămase se bazează pe regula 1 și pe regulile de operare cu vectori.

Exemplul 1.1: Având în vedere o funcție vectorială.Construiți odograful său și creați o ecuație pentru tangenta sa într-un punct arbitrar.

Soluţie. Pentru orice punct ( X , y , z ) vector hodograf – funcții avem:X = cost ; y = asint ; z = bt si deci pentru orice
egalitatea este valabilăX 2 + y 2 = A 2 , iar generatoarea este paralelă cu axa Oz. Dacă parametrul t interpretat ca timp, apoi cu mișcare uniformă în jurul unui cerc proiecția capătului vectorului rază pe planOxy proiecția sa pe axăOz se va mișca uniform și rectiliniu cu vitezăb . Cu alte cuvinte, aplicarea unui punct hodograf al unei funcții vectoriale crește proporțional cu unghiul de rotație al proiecției sale pe plan.Oxy . Prin urmare, hodograful dorit va avea forma prezentată în Fig. 3 și se numește linie elicoială. Pentru a găsi tangentele la hodograf (linia elicoidală), găsim derivata funcției vectoriale.

Soluţie. Deoarece, apoi

Definiția 1. Vectorul g se numește funcție vectorială a argumentului scalar t dacă fiecare valoare a scalarului din intervalul de valori admisibile corespunde unei anumite valori a vectorului r. O vom scrie astfel: Dacă vectorul r este o funcție a argumentului scalar t, atunci coordonatele x, y, z ale vectorului g sunt și funcții ale argumentului t: Funcția vectorială a argumentului scalar. Hodograf. Limita și continuitatea funcției vectoriale a unui argument scalar.În schimb, dacă coordonatele vectorului g sunt funcții ale lui t%, atunci vectorul g însuși va fi o funcție a lui t: Astfel, specificând funcția vectorială r(f) este echivalent cu specificarea a trei funcții scalare y(t), z(t). Definiția 2. Hodograful unei funcții vectoriale r(t) a unui argument scalar este locul punctelor care descrie sfârșitul vectorului r(*) când scalarul t se modifică, când începutul vectorului r(f) este plasat într-un punct fix O în spațiu (Fig. I ). Hodograf de dragul mișcării vectorului mustață r = g(*) Fig. 1 punct de ardere va fi traiectoria L a acestui punct în sine. Hodograful vitezei v = v(J) a acestui punct va fi o altă linie L\ (Fig. 2). Deci, dacă un punct material se mișcă într-un cerc cu o viteză constantă |v| = const, atunci hodograful său de viteză este tot un cerc cu centrul în punctul 0\ și cu raza egală cu |v|. Exemplul 1. Construiți o hodografă a vectorului r = ti + t\ + t\. Soluţie. 1. Aceasta constructie se poate face punct cu punct, alcatuind un tabel: Fig. 3 2i La fel puteti face. Notând coordonatele vectorului V cu x, y, z, vom avea Hts Și cheie din aceste ecuații este parametrul 1Y obținem ecuațiile suprafețelor y - z = x1, a căror linie de intersecție L va determina hodograful a vectorului z() (Fig. 3). D> Sarcini pentru soluție independentă. Construiți hodografe de vectori: Fie ca funcția vectorială r = argument scalar t să fie definită într-o vecinătate a valorii to a argumentului t, cu excepția, poate, pentru aceeași valoare, extensia 1. Vectorul constant А se numește limita vector r(t) at, dacă pentru orice e > 0 există b > 0 astfel încât pentru tot t φ până la satisfacerea condiției 11, inegalitatea este valabilă. Ca și în analiza convențională, scrieți limr(0=A. Fig. 4 Geometric, aceasta înseamnă că vectorul) ca t -* to tinde spre vectorul Și atât în ​​lungime cât și în direcție (Fig. 4). Definiția 2. Se spune că vectorul a(£) este infinitezimal la t -» to dacă a(£) are o limită la t -* to și această limită este egală cu zero: Funcția vectorială a unui argument scalar. Hodograf. Limita și continuitatea unei funcții vectoriale a unui argument scalar sau, care este același, pentru orice e există 6 > 0 astfel încât pentru tot t Ф la îndeplinirea condiției, inegalitatea |a(£)| exemplu 1. Arătați că vectorul este un vector infinit stacojiu pentru t -* 0. Soluție. Avem unde este clar că dacă pentru orice e 0 luăm 6 = ~, atunci la -0| vom marca |. Conform definiției, aceasta înseamnă că a(t) este un vector infinit la t 0. 1> probleme pentru rezolvarea independentă a lui r. Să se arate că limita modulului unui vector este egală cu modulul limitei sale dacă ultima limită există. . Demonstrați că pentru ca funcția vectorială r(*) să aibă o limită A este necesar și suficient ca r(să poată fi reprezentat sub forma Funcție vectorială a unui argument scalar. Hodograf. Limita și continuitatea unei funcții vectoriale a unui argument scalar de a( t) - muta vectorul la nesfârșit pentru t -* t0. 14. Funcția vectorială a+ b(*) este continuă pentru t = t0. Rezultă de aici că vectorii a(t) și b( J) sunt de asemenea continue pentru t - la ? 15. Demonstrați că dacă a( sunt funcții vectoriale continue, atunci produsul lor scalar (a(*),b(f)) și produsul vectorial |a(f),b(t )] sunt de asemenea continue.

și diferențierea acesteia.

Una dintre cele mai simple moduri de a specifica o curbă spațială este de a specifica o ecuație vectorială:

Unde este vectorul rază al punctului curbei și - parametru care determină poziția punctului.

Acea. vector variabil există o funcție scalară . În analiza matematică, astfel de funcții sunt numite funcții vectoriale ale unui argument scalar.

În descompunere folosind vectori unitari, ecuația (1) poate fi dată sub forma:

Această expansiune face posibilă trecerea la ecuația parametrică a curbei:

Cu alte cuvinte, specificarea unei funcții vectoriale este echivalentă cu specificarea a trei funcții scalare.

În raport cu funcția vectorială (1) care definește această curbă, curba însăși se numește hodograful acestei funcții. Originea coordonatelor se numește în acest caz polul hodografului.

Lasă-l acum
Și
- puncte ale curbei definite de ecuația (1). Și
, A
Vectorii de rază ai acestor puncte vor fi

Și
.

Vector
numită incrementul unei funcții vectoriale
, corespunzător incrementului
argumentul său și este notat cu
,

Funcția vectorială
va fi o funcție continuă , Dacă

.

Pentru a găsi derivata lui
hai sa procedam dupa cum urmeaza -

.

Acum să stabilim direcția
. Este evident că coliniar cu
iar la
îndreptată în aceeaşi direcţie ca
iar la
- în sens invers. Dar în primul caz
iar în al doilea
Acea. vector întotdeauna îndreptată de-a lungul odografului secant
în sus .

Dacă folosim expansiunea Și prin orts, atunci

De aici împărțind (*) la
și mergând la limită
Pentru
primim

Pe baza (4), se poate demonstra că următoarele formule sunt valabile:

(5)

(6)

- functie scalara.

Dovada (7).

Să examinăm acum câteva proprietăți
. În primul rând, să-i găsim modulul:

.

Deoarece atunci considerăm că arcul hodograf este rectificabil
- este lungimea coardei și
- lungimea arcului. De aceea

Acea. modulul derivatei funcției vectoriale a unui argument scalar este egal cu derivata arcului odograf față de același argument.

Corolarul 1. Dacă - vector unitar îndreptat tangenţial la hodograf în sensul creşterii , Acea

Corolarul 2. Dacă lungimea arcului odograf este luată ca argument al funcției vectoriale , Acea

(deoarece
)

Acea. derivata funcției vectoriale de-a lungul lungimii arcului hodografului este egală cu vectorul unitar al tangentei la hodograf, îndreptată spre creșterea lungimii arcului.

Corolarul 3. Dacă hodograful unei funcții vectoriale este considerat ca traiectoria unui punct și - ca timp de mișcare, numărat de la un anumit , Acea
coincide ca mărime și direcție cu vectorul viteză a mișcării
.

De fapt, valoarea scalară a vitezei este egală cu derivata căii în raport cu timpul:

În plus, vectorul îndreptate tangenţial la traiectoria în direcţia de mişcare, care corespunde direcţiei de creştere , adică corespunde directiei .

Acea.
.

Luați în considerare acum
, a cărui lungime este constantă,
, adică

(*)
Unde

Diferențiând (*), găsim:

Acestea.

În special, derivata unui vector a oricărei variabile în direcția unității Mereu
.

Lasă-l acum
unghiul dintre razele sferei unitare trasate la puncte
Și
odograf
. Apoi lungimea acordului
dintr-un triunghi
va fi egal

Mărimea derivatei unui vector variabil unitar este egală cu viteza unghiulară de rotație a acestui vector.

În ceea ce privește funcțiile scalare, diferența unei funcții vectoriale se scrie ca

Dar chiar și atunci

Curbura unei curbe spațiale.

Triedrul însoțitor.

Conform Corolarul 2, pt putem scrie formula:

Schimbarea direcției , asociat cu o modificare a tangentei la curba spațială, caracterizează curbura curbei. Ca măsură a curburii unei curbe spațiale, ca și pentru o curbă plană, se ia limita raportului dintre unghiul de adiacentă și lungimea arcului, când

curbură,
unghiul de adiacenta,
lungimea arcului.

Pe de alta parte,
vector unitar și vectorul său derivat este perpendicular pe acesta și modulul său
Diferențierea De și intrând
vector unitar cu direcție , găsim:

Vector
vector de curbură al unei curbe spațiale. Direcția sa, perpendiculară pe direcția tangentei, este direcția normală a curbei spațiului. Dar o curbă spațială are în orice punct un număr infinit de normale, care se află toate într-un plan care trece printr-un punct dat al curbei și perpendiculare pe tangenta într-un punct dat. Acest plan se numește planul normal al curbei spațiale.

Definiție. Normala curbei de-a lungul căreia este îndreptat vectorul de curbură al curbei într-un punct dat este normala principală a curbei spațiale. Acea.
vectorul normal principal al unității.

Să construim acum al treilea vector unitar egal cu produsul încrucișat Și

Vector , ca de asemenea perpendicular acestea. se află în plan normal. Direcția sa se numește direcția binormalului curbei spațiale într-un punct dat. Vector
Și constituie un trio de vectori unitari reciproc perpendiculari, a căror direcție depinde de poziția punctului pe curba spațială și variază de la un punct la altul. Acești vectori formează așa-numitul. triedrul însoțitor (triedrul Frenet) al unei curbe spațiale. Vector
Și formează un triplu drept, la fel ca vectorii unitari
în sistemul de coordonate corect.

Luat în perechi
definiți trei plane care trec prin același punct de pe curbă și formează fețele triedrului însoțitor. în care Și determinați planul osculator (arcul unei curbe în vecinătatea unui punct dat este arcul unei curbe plane în planul osculator cu o precizie de ordin superior);

Și - plan de îndreptare;

Și - plan normal.

Ecuații tangente, normale și binormale.

Ecuațiile planelor triedrului însoțitor.

știind
Și , sau orice vector non-unitar coliniar cu acestea T, NȘi B Să derivăm ecuațiile numite în această secțiune.

Pentru a face acest lucru, în ecuația canonică a dreptei

iar în ecuaţia planului care trece printr-un punct dat

a lua pentru
coordonatele punctului selectat pe curbă, pt
sau respectiv pentru
se iau coordonatele celei ale vectorilor
sau
, care determină direcția dreptei dorite sau normală la planul dorit:

sau - pentru un plan tangent sau normal,

sau - pentru planul normal principal și de îndreptare,

sau - pentru plan binormal si osculator.

Dacă curba este dată de ecuația vectorială
sau
apoi pentru vector
dirijate tangențial pot fi luate

A găsi
Și să găsim mai întâi descompunerea
prin vectori
Anterior (Corolarul 1) am constatat că
Diferențierea prin , primim:

Dar, pentru că

Să înmulțim acum vectorial Și

(*)

Pe baza (*) pe vector , având o direcție binormală, am putea lua vectorul

Dar apoi, pentru
putem lua produsul vectorial al acestora din urmă:

Acea. în orice punct al unei curbe arbitrare putem determina toate elementele triedrului însoțitor.

Exemplu. Ecuația tangentei, normale și binormale la helixul drept în orice punct.

Tangentă

Acasă normală

Binormal

Să se reducă setul de valori ale funcției vectoriale a argumentului scalar la o origine comună în punctul 0. Să potrivim originea sistemului de coordonate carteziene cu acest punct. Apoi, pentru orice vector poate fi extins în vectori unitari

Astfel, specificarea unei funcții vectoriale a unui argument scalar înseamnă specificarea a trei funcții scalare Când valoarea argumentului se schimbă, sfârșitul vectorului va descrie o curbă în spațiu, care se numește hodograf vectorial

Să existe o valoare apropiată pentru Apoi derivata unei funcții vectoriale la un argument scalar este numită

Nr. 17 Viteza și accelerația unui punct în mișcare curbilinie

Viteză

Viteza este introdusă ca o caracteristică a mișcării unui punct material. Viteza este o mărime vectorială, care se caracterizează atât prin viteza de mișcare (mărimea vectorului viteză), cât și prin direcția acesteia (direcția vectorului viteză) la un moment dat. Fie ca un punct material să se deplaseze de-a lungul unei traiectorii curbilinii, iar în momentul de timp t corespunde vectorului rază r0 (Fig. 1). Într-o perioadă scurtă de timp Δt, punctul va călători Δs și, în același timp, va primi o deplasare elementară (infinitesimală) Δr.

Vector viteză medie se numește raportul dintre incrementul Δr al vectorului rază al unui punct și intervalul de timp Δt:

Direcția vectorului viteză medie coincide cu direcția lui Δr. Cu o scădere infinită a Δt, viteza medie tinde către o valoare numită viteza instantanee v:

Aceasta înseamnă că viteza instantanee v este o mărime vectorială, care este egală cu prima derivată a vectorului rază a punctului în mișcare în raport cu timpul. Deoarece în limită, secanta coincide cu tangenta, apoi vectorul viteză v este direcționat tangent la traiectorie în sensul deplasării (fig. 2).

Fig.2

Pe măsură ce Δt scade, Δs se va apropia din ce în ce mai mult de |Δr|, astfel încât modulul de viteză instantanee

Aceasta înseamnă că valoarea absolută a vitezei instantanee este egală cu prima derivată a căii în raport cu timpul:

Cu o mișcare neuniformă, modulul de viteză instantanee este diferit în momente diferite. În acest caz, utilizați mărimea scalară - viteza medie a mișcării inegale:

Dacă integrăm expresia ds=vdt în timp în intervalul de la t la t+Δt (vezi formula (2)), vom găsi lungimea drumului parcurs de punct în timpul Δt:

În cazul mișcării uniforme, valoarea numerică a vitezei instantanee este constantă; Atunci expresia (3) va lua forma

Lungimea traseului parcurs de un punct în perioada de timp de la t1 la t2 este dată de integrală

ACCELERARE

Când conduceți neuniform, este adesea necesar să știți cât de repede se schimbă viteza în timp. O mărime fizică care caracterizează rata de schimbare a vitezei în mărime și direcție se numește accelerație. Să considerăm mișcarea plană - mișcare în care traiectoriile fiecărui punct al sistemului luat în considerare se află în același plan. Fie vectorul v viteza punctului A la momentul t. În timpul Δt, punctul s-a mutat în poziția B și a primit o viteză diferită de v atât ca mărime, cât și ca direcție și egală cu v1 + Δv. Să mutăm vectorul v1 în punctul A și să găsim Δv (Fig. 1).

Accelerația medie a mișcării neuniforme în intervalul de la t la t+Δt este o mărime vectorială egală cu raportul dintre modificarea vitezei Δv și intervalul de timp Δt:

Accelerația instantanee a (accelerația) a unui punct material la momentul t va fi o mărime vectorială:

egală cu derivata întâi a vitezei în raport cu timpul.

Să descompunăm vectorul Δv în două componente. Pentru a face acest lucru, din punctul A (Fig. 1) în direcția vitezei v, trasăm vectorul AD, al cărui modul este egal cu v1. Evident, vectorul CD egal cu Δvτ determină modificarea vitezei în timp Δt modulo: Δvτ=v1-v. A doua componentă Δvn a vectorului Δv caracterizează schimbarea vitezei în timp Δt în direcție.

Componenta accelerației tangențiale:

adică este egal cu prima derivată în raport cu timpul modulului de viteză, determinând astfel rata de schimbare a vitezei în modul.

Căutăm a doua componentă a accelerației. Presupunem că punctul B este foarte aproape de punctul A, deci Δs poate fi considerat un arc de cerc cu o rază r, ușor diferită de coarda AB. Triunghiul AOB este similar cu triunghiul EAD, din care rezultă Δvn/AB=v1/r, dar deoarece AB=vΔt, atunci

În limita la Δt→0 obținem v1→v.

Deoarece v1→v, unghiul EAD tinde spre zero, iar din moment ce triunghiul EAD este isoscel, atunci unghiul ADE dintre v și Δvn tinde spre un unghi drept. În consecință, la Δt→0 vectorii Δvn și v devin reciproc perpendiculari. Deoarece vectorul viteză este direcționat tangențial la traiectorie, apoi vectorul Δvn, perpendicular pe vectorul viteză, este direcționat către centrul de curbură al traiectoriei punctului. A doua componentă a accelerației, egală cu

se numeste componenta normala a acceleratiei si este indreptata de-a lungul unei drepte perpendiculare pe tangenta traiectoriei (numita normala) la centrul curburii acesteia (de aceea se mai numeste si acceleratie centripeta).

Accelerația totală a corpului este suma geometrică a componentelor tangențiale și normale (Fig. 2):

Aceasta înseamnă că componenta tangenţială a acceleraţiei este o caracteristică a ratei de schimbare a vitezei în valoare absolută (direcţionată tangenţial la traiectorie), iar componenta normală a acceleraţiei este o caracteristică a ratei de schimbare a vitezei în direcţie (direcţionată către centrul de curbură al traiectoriei). În funcție de componentele tangențiale și normale ale accelerației, mișcarea poate fi clasificată după cum urmează:

1)aτ=0, an=0 - mișcare uniformă rectilinie;

2)aτ=an=const, аn=0 - mișcare uniformă rectilinie. Cu acest tip de mișcare

Dacă timpul inițial t1 = 0, iar viteza inițială v1 = v0, atunci, notând t2=t și v2 = v, obținem a=(v-v0)/t, din care

După ce am integrat această formulă în intervalul de la zero la un moment arbitrar de timp t, aflăm că lungimea drumului parcurs de un punct în cazul mișcării uniform variabile

3)aτ=f(t), an=0 - mișcare rectilinie cu accelerație variabilă;

4)aτ=0, an=const. Când aτ=0, viteza nu se modifică în valoare absolută, ci se schimbă în direcție. Din formula an=v2/r rezultă că raza de curbură trebuie să fie constantă. Prin urmare, mișcarea circulară este uniformă, mișcarea curbilinie uniformă;

5)aτ=0, an≠0 mișcare curbilinie uniformă;

6)aτ=const, an≠0 - mișcare uniformă curbilinie;

7)aτ=f(t), an≠0 - mișcare curbilinie cu accelerație variabilă.

Nr. 18 Ecuațiile planului tangent și ale normalei la suprafață

Definiție. Fie dată o funcție a două variabile z =f(x,y) pe un domeniu D, M0(x0;y0) este un punct intern al domeniului D, M(x0+Δx;y+Δy) este un punct în D „învecinat” M0.

Luați în considerare creșterea completă a funcției:

Dacă Δz este reprezentat ca:

unde A, B sunt constante (independente de Δx, Δy), - distanta dintre M si M0, α(Δ x,Δy) - infinitezimal la Δx 0, Δy 0; atunci functia z =f(x,y) se numeste diferentiabila in punctul M0, iar expresia

se numeste diferenta totala a functiei z =f(x;y) in punctul M0.

Teorema 1.1. Dacă z =f(x;y) este diferențiabilă în punctul M0, atunci

Dovada

Deoarece în (1.16) Δx, Δy sunt infinitezimale arbitrare, putem lua Δy =0, Δx≠0, Δx 0, atunci

după care din (1.16) rezultă

În mod similar, este dovedit că

și Teorema 1.1. dovedit.

Notă: diferențiabilitatea lui z =f(x,y) în punctul M0 implică existența derivatelor parțiale. Afirmația inversă este falsă (existența derivatelor parțiale în punctul M0 nu implică diferențiabilitate în punctul M0).

Ca rezultat, luând în considerare teorema 1.1, formula (1.18) va lua forma:

Consecinţă. O funcție diferențiabilă în punctul M0 este continuă în acest punct (deoarece din (1.17) rezultă că pentru Δx 0, Δy 0: Δz 0, z(M) z(M0)).

Notă: În mod similar, în cazul a trei sau mai multe variabile. Expresia (1.17) va lua forma:

Folosind semnificația geometrică (Fig. 1.3) a derivatelor parțiale, putem obține următoarea ecuație (1.24) a planului tangent πcass la suprafață: z =f(x,y) în punctul C0(x0,y0,z0), z0=z(M):

Dintr-o comparație a (1.24) și (1.21) obținem semnificația geometrică a diferenţialului total al unei funcţii a două variabile:

Creșterea aplicației z când punctul C se mișcă de-a lungul unui plan tangent de la punctul C0 la punctul

unde este de la (1.24).

Ecuația normalei Lн la suprafață: z = f(x,y) în punctul C0 se obține ca ecuație a unei drepte care trece prin C0 perpendicular pe planul tangent:

Nr. 19 Derivată direcțională. Gradient

Fie dată o funcție într-un anumit domeniu și punct . Să desenăm un vector din punctul a cărui direcție cosinus . Pe vectorul , la o distanță de originea lui, se consideră punctul , i.e. .

Vom presupune că funcția iar derivatele sale parțiale de ordinul întâi sunt continue în domeniu.

Limita relației la se numește derivată a funcției la punct în direcția vectorului și se notează cu , i.e. .

Pentru a găsi derivata unei funcții la un punct dat în direcția vectorului utilizați formula:

Unde sunt cosinusurile de direcție ale vectorului , care sunt calculate prin formulele:
.

Lasă funcția .

Un vector ale cărui proiecții pe axele de coordonate sunt valorile derivatelor parțiale ale acestei funcții în punctul corespunzător se numește gradient al funcției și este desemnată sau (a se citi „nabla u”): .

În acest caz, ei spun că un câmp vectorial de gradienți este definit în regiune.

Pentru a găsi gradientul unei funcții la un punct dat utilizați formula: .

Nr. 22 proprietăți de bază ale integralei nedefinite

Integrală nedefinită

unde F este antiderivată a funcției f (pe interval); C este o constantă arbitrară.

Proprietăți de bază

1.

2.

3. Dacă Acea

24)

25)

28)

Această metodă este utilizată în cazurile în care integrandul este un produs sau un coeficient de funcții eterogene. În acest caz, V’(x) este considerat a fi partea care este ușor de integrat.

29)

32) Descompunerea unei fracții raționale în fracții simple.

Orice fracție rațională adecvată
poate fi reprezentat ca suma unui număr finit de fracții raționale simple ale primului – al patrulea tip. Pentru descompunere
este necesară extinderea numitorului în fracții simple Qm(x)în factori liniari și pătrați, pentru care trebuie să rezolvați ecuația:

- (5)

Teorema.Fracția rațională proprie
, Unde
, poate fi descompus în mod unic într-o sumă de fracții simple:

- (6)

(A 1 , A 2 , …, A k , B 1 , B 2 , …, B 1 , M 1 , N 1 , M 2 , M 2 , …, M s , N s – unele numere reale).

33) Descompunerea unei fracții proprii în fracții simple cu rădăcini complexe ale numitorului

Formularea problemei. Aflați integrala nedefinită

1 . Să introducem următoarea notație:

Să comparăm gradele numărătorului și numitorului.

Dacă integrandul este o fracție rațională improprie, i.e. gradul de numărătorn mai mare sau egală cu puterea numitoruluim , apoi selectăm mai întâi întreaga parte a funcției raționale împărțind numărătorul la numitor:

Aici polinomul este restul împărțirii prin și gradulPk(x) grad mai micQm

2 . Să extindem fracția rațională adecvată

la fracții elementare.

Dacă numitorul său are rădăcini complexe simple i.e.

atunci expansiunea are forma

3 . Pentru a calcula coeficienți nesiguri,A1,A2,A3...B1,B1,B3... aducem fracția din dreapta identității la un numitor comun, după care echivalăm coeficienții la aceleași puteriX în numărătorii din stânga și din dreapta. Să luăm sistemul 2 S ecuatii cu 2 S necunoscut, care are o soluție unică.

4 Integram fractii elementare ale formei

47) Dacă există o limită finită I a sumei integrale ca λ → 0, și nu depinde de metoda de alegere a punctelor ξ i, metoda de împărțire a segmentului, atunci această limită se numește integrală definită a funcției f ( x) peste segment și se notează după cum urmează:

În acest caz, se spune că funcția f (x) este integrabilă pe . Numerele a și b se numesc limitele inferioare și superioare ale integrării, respectiv, f (x) este integrandul, x este variabila integrării. Trebuie remarcat că nu contează ce literă denotă variabila de integrare a unei integrale definite

întrucât modificarea notaţiilor de acest fel nu afectează în niciun fel comportamentul sumei integrale. În ciuda asemănării în notație și terminologie, integralele definite și nedefinite sunt diferite

48) Teoremă privind existența unei integrale definite

Să împărțim segmentul în părți prin punctele x1,x2,x3... deci

Să notăm cu deltaX lungimea piesei i-a și cu maximul acestor lungimi.

Să selectăm în mod arbitrar un anumit punct pe fiecare segment, astfel încât (se numește „punctul de mijloc”) și să compunem

o cantitate numită sumă integrală

Să găsim limita acum

Definiție. Dacă există și nu depinde de

a) metoda de împărțire a unui segment în părți și din

b) metoda de alegere a punctului de mijloc,

este o integrală definită a funcției f(x) peste segmentul .

Funcția f(x) se numește în acest caz integrabilă pe interval. Mărimile a și b se numesc limite inferioară și, respectiv, superioară de integrare.

50) Proprietățile de bază ale unei integrale definite

1) Dacă intervalul de integrare este împărțit într-un număr finit de intervale parțiale, atunci integrala definită preluată în interval este egală cu suma integralelor definite preluate în toate intervalele sale parțiale.

2) teorema valorii medii.

Fie funcția y = f(x) integrabilă pe intervalul ,m=min f(x) și M=max f(x), atunci există un astfel de număr

Consecinţă.

Dacă funcția y = f(x) este continuă pe intervalul , atunci există un număr astfel încât.

3) La rearanjarea limitelor integrării, integrala definită își schimbă semnul în opus.

4) O integrală definită cu aceleași limite de integrare este egală cu zero.

5) Integrarea modulului funcțional

Dacă funcția f(x) este integrabilă, atunci modulul său este și integrabil pe interval.

6) Integrarea inegalității

Dacă f(x) și q(x) sunt integrabile pe un interval și căreia x îi aparține

Acea

7) Linearitate

Factorul constant poate fi luat dincolo de semnul integralei definite

dacă f(x) există și este integrabil pe interval, A=const

Dacă funcția y=f(x) este continuă pe un interval și F(x) este oricare dintre antiderivatele sale pe (F’(x)=f(x)), atunci formula este valabilă

Să se facă substituția x=α(t) pentru a calcula integrala unei funcții continue.

1) Funcția x=α(t) și derivata ei x’=α’(t) sunt continue pentru t aparținând lui

2) Mulțimea de valori ale funcției x=α(t) la t aparține segmentului

3) A α(c)=a și α(v)=b

Fie funcția f(x) continuă pe interval și are o discontinuitate infinită la x=b. Dacă există o limită, atunci se numește integrală improprie de al doilea fel și se notează cu .

Astfel, prin definiție,

Dacă există limita din partea dreaptă, atunci integrala necorespunzătoare converge. Dacă limita specificată nu există sau este infinită, atunci ei spun că integrala diverge.

Exemplul 2 Luați în considerare, de exemplu, o funcție a trei variabile f(X,la,z), având următorul tabel de adevăr:

Cu ordinea lexicografică a vectorilor de valori variabile  X n acestea pot fi omise și funcția va fi complet specificată de ea vector al valorilor de adevăr f= (10110110).

Metoda matricei

Ideea este că multe variabile  X n se desparte în două părți  la mȘi  z n–m astfel încât toate valorile de adevăr posibile ale vectorului  la m sunt reprezentate de-a lungul rândurilor matricei și toate valorile de adevăr posibile ale vectorului  z n - m- pe coloane. Valori de adevăr ale funcției f pe fiecare set   n = ( 1 , ...,  m ,  m+ 1 ,...,  n) plasate în celulele formate prin intersecţia liniei ( 1 , ...,  m) si coloana ( m+ 1 ,...,  n).

În Exemplul 2 discutat mai sus, în cazul variabilelor de partiționare ( x, y, z) în subseturi ( X) Și ( y,z) matricea ia forma:

	y,z

O caracteristică esențială a metodei matricei este aceea că se completează seturi de variabile  X n, corespunzătoare celulelor învecinate (atât pe verticală, cât și pe orizontală) diferă într-o coordonată.

Specificarea utilizării unui arbore binar complet

Pentru descriere n-functie locala f( X n) se folosește proprietatea de înălțime a unui arbore binar n, care constă în faptul că fiecare vârf de pandantiv din el corespunde unu-la-unu unui anumit set de valori vectoriale  X n. În consecință, acestui vârf suspendat i se poate atribui aceeași valoare de adevăr pe care o are funcția pe acest set f. Ca exemplu (Fig. 1.3), prezentăm o sarcină folosind un arbore binar al funcției ternare discutate mai sus f =(10110110).

Primul rând de numere atribuite vârfurilor suspendate ale arborelui denotă numărul lexicografic al setului, al doilea - setul în sine, iar al treilea - valoarea funcției de pe acesta.

Utilizarea sarciniin - cub de unitate dimensionalăÎN n

De la vârfuri ÎN n poate fi, de asemenea, mapat unu-la-unu la setul de toate seturile  X n, Acea n-functie locala f(X n) poate fi specificat prin atribuirea valorilor sale de adevăr la vârfurile corespunzătoare ale cubului ÎN n . Figura 1.4 arată setarea funcției f= (10110110) în Cuba ÎN 3 . Valorile de adevăr sunt atribuite vârfurilor cubului.

Definiție . Algebra logicii numiți un set de constante și variabile booleene împreună cu conexiunile logice introduse pe ele.

Sarcină de formulă

Funcțiile de algebră logică pot fi specificate ca expresii analitice.

Definiție. Lăsa X― alfabetul variabilelor și constantelor utilizate în algebra logică, F― un set de notații pentru toate funcțiile elementare și generalizările acestora cu un număr de variabile care depășește 2.

Formula peste X,F(formula de algebră logică) să apelăm toate înregistrările din formularul:

A) X, Unde X X;

b)  F 1 , F 1 &F 2 ,F 1 F 2 , F 1 F 2 , F 1  F 2 , F 1 F 2 ,F 1 F 2 ,F 1 F 2 , Unde F 1 , F 2 - formule peste X, F;

V) h(F 1 , … ,F n ), Unde n > 2, F 1 ,… ,F n- formule peste X,F, h ― denotarea funcţiei de prag generalizat din F .

După cum reiese din definiție, pentru funcțiile elementare cu două locuri se folosește forma de notație infixă, în care simbolul funcțional este plasat între argumente; pentru funcțiile de negație și generalizate se folosește forma de notație prefixă, în care simbolul funcțional. este plasat înaintea listei de argumente.

Exemplul 3

1. Expresii X(laz); ( X, y, z  u) sunt formule ale algebrei logicii, deoarece satisfac definiția dată mai sus.

2. Expresia  X (la z) nu este o formulă de algebră logică deoarece operația  a fost aplicată incorect .

Definiție. Funcția implementată prin formula F, este funcția obținută prin înlocuirea valorilor variabilelor în F. Să o notăm f(F).

Exemplul 4 Luați în considerare formula F=hu (Xz). Pentru a construi tabelul de adevăr al funcției implementate, este necesar să se efectueze înmulțirea logică secvențială, ținând cont de puterea conectivelor logice. hu, apoi implicația ( Xz), apoi adăugați valorile de adevăr rezultate în modulul 2. Rezultatul acțiunilor este afișat în tabel:

				X z

Reprezentarea prin formulare a funcțiilor permite evaluarea a priori a multor proprietăți ale funcțiilor. Trecerea de la o sarcină formulă la un tabel de adevăr poate fi întotdeauna realizată prin substituții succesive ale valorilor de adevăr în funcții elementare incluse în formulă. Tranziția inversă este ambiguă, deoarece aceeași funcție poate fi reprezentată prin formule diferite. Este nevoie de o analiză separată.