Acasă » clasa a 8-a » Ce înseamnă să exprimi un vector în termenii altor doi. Vectori pentru manechine. Acțiuni cu vectori. Coordonatele vectoriale. Cele mai simple probleme cu vectorii. Cum se află lungimea sumei vectorilor

Ce înseamnă să exprimi un vector în termenii altor doi. Vectori pentru manechine. Acțiuni cu vectori. Coordonatele vectoriale. Cele mai simple probleme cu vectorii. Cum se află lungimea sumei vectorilor

Într-un paralelogram, un punct se află pe latura , . Exprimați vectorul în termeni de vectori și .

Rezolvarea problemei

Această lecție arată cum se exprimă un segment arbitrar prin vectorii cunoscuți sub forma laturilor unui paralelogram ca o compoziție a vectorilor originali. Aceasta sarcina nu am putea avea o soluție dacă nu am ști în ce raport se împarte una dintre laturile paralelogramului la un punct aparținând segmentului dorit. Acțiunile ulterioare se reduc la determinarea începutului și sfârșitului vectorilor dați și a vectorilor în care este împărțită latura. Toate acestea sunt necesare pentru a utiliza corect semnele la combinarea vectorilor. La urma urmei, este necesar să ne amintim regulile de adunare a vectorilor: suma vectorilor dă un al treilea vector, începutul căruia coincide cu începutul primului vector și sfârșitul cu sfârșitul celui de-al doilea; iar regula de scădere a vectorilor: diferența a doi vectori este al treilea vector, începutul căruia coincide cu capetele celui de-al doilea vector, iar sfârșitul cu sfârșitul primului vector. Pe baza acestor reguli simple, putem obține combinația de care avem nevoie.

Vor exista și sarcini pentru o soluție independentă, la care puteți vedea răspunsurile.

Concept de vector

Înainte de a afla totul despre vectori și operațiunile pe ei, acordați-vă pentru a rezolva o problemă simplă. Există un vector al întreprinderii tale și un vector al abilităților tale inovatoare. Vectorul antreprenoriatului te conduce la Scopul 1, iar vectorul abilităților inovatoare - la Scopul 2. Regulile jocului sunt de așa natură încât să nu te poți deplasa în direcțiile acestor doi vectori deodată și să atingi două obiective deodată. Vectorii interacționează sau, vorbind matematic, se efectuează o operațiune asupra vectorilor. Rezultatul acestei operațiuni este vectorul „Rezultat”, care vă duce la Obiectivul 3.

Acum spuneți-mi: rezultatul cărei operațiuni pe vectorii „Întreprindere” și „Abilități inovatoare” este vectorul „Rezultat”? Dacă nu poți spune imediat, nu te descuraja. Pe măsură ce studiezi această lecție, vei putea răspunde la această întrebare.

După cum am văzut mai sus, vectorul vine în mod necesar dintr-un punct Aîn linie dreaptă până la un punct B. În consecință, fiecare vector are nu numai o valoare numerică - lungime, ci și o direcție fizică și geometrică. Din aceasta se derivă prima, cea mai simplă definiție a unui vector. Deci, un vector este un segment direcționat care merge dintr-un punct A până la punctul B. Este marcat astfel:

Și să încep altfel operații vectoriale , trebuie să ne familiarizăm cu încă o definiție a unui vector.

Un vector este un fel de reprezentare a unui punct care trebuie atins dintr-un punct de plecare. De exemplu, un vector tridimensional este de obicei scris ca (x, y, z) . Mai simplu spus, aceste numere reprezintă cât de departe trebuie să mergi în trei direcții diferite pentru a ajunge la obiect.

Fie dat un vector. în care X = 3 (mâna dreaptă arată spre dreapta) y = 1 (mâna stângă puncte înainte) z = 5 (sub punct există o scară care duce sus). Din aceste date, vei găsi punctul mergând 3 metri în direcția indicată de mâna dreaptă, apoi 1 metru în direcția indicată de mâna stângă, iar apoi te așteaptă o scară și, urcând 5 metri, vei găsi în sfârșit. tu însuți la punctul final.

Toți ceilalți termeni sunt perfecționări ale explicației prezentate mai sus, necesare pentru diferite operații pe vectori, adică pentru rezolvarea unor probleme practice. Să trecem prin aceste definiții mai riguroase, insistând asupra problemelor tipice vectoriale.

Exemple fizice cantitățile vectoriale pot servi drept părtinire punct material deplasarea în spațiu, viteza și accelerația acestui punct, precum și forța care acționează asupra acestuia.

vector geometric reprezentat în spaţiu bidimensional şi tridimensional în formă segment dirijat. Acesta este un segment care are un început și un sfârșit.

Dacă A este începutul vectorului și B este sfârșitul său, atunci vectorul este notat cu simbolul sau o singură literă minusculă . În figură, sfârșitul vectorului este indicat printr-o săgeată (Fig. 1)

Lungime(sau modul) a unui vector geometric este lungimea segmentului care îl generează

Cei doi vectori se numesc egal , dacă pot fi combinate (când direcţiile coincid) prin translaţie paralelă, adică. dacă sunt paralele, punctează în aceeași direcție și au lungimi egale.

În fizică, este adesea luat în considerare vectori fixați, punct aplicații, lungime și direcție. Dacă punctul de aplicare al vectorului nu contează, atunci acesta poate fi transferat, păstrând lungimea și direcția în orice punct din spațiu. În acest caz, vectorul este numit gratuit. Suntem de acord să luăm în considerare numai vectori liberi.

Operații liniare pe vectori geometrici

Înmulțiți un vector cu un număr

Produs vectorial pe număr Un vector se numește vector obținut dintr-un vector prin întindere (la ) sau micșorare (la ) ori, iar direcția vectorului este păstrată dacă , și inversată dacă . (Fig. 2)

Din definiție rezultă că vectorii și = sunt întotdeauna situați pe una sau drepte paralele. Astfel de vectori se numesc coliniare. (De asemenea, se poate spune că acești vectori sunt paraleli, dar în algebra vectorială se obișnuiește să se spună „coliniar”.) Este adevărat și invers: dacă vectorii și sunt coliniari, atunci ei sunt legați prin relația

Prin urmare, egalitatea (1) exprimă condiția de coliniaritate a doi vectori.

Adunarea și scăderea vectorului

Când adăugați vectori, trebuie să știți asta sumă vectori și se numește vector al cărui început coincide cu începutul vectorului, iar sfârșitul coincide cu sfârșitul vectorului, cu condiția ca începutul vectorului să fie atașat de sfârșitul vectorului. (Fig. 3)

Această definiție poate fi distribuită pe orice număr finit de vectori. Lăsați în spațiu dat n vectori liberi. Când se adună mai mulți vectori, suma lor este luată ca vector de închidere, începutul căruia coincide cu începutul primului vector și sfârșitul cu sfârșitul ultimului vector. Adică, dacă începutul vectorului este atașat la sfârșitul vectorului, iar începutul vectorului la sfârșitul vectorului etc. și, în sfârșit, până la sfârșitul vectorului - începutul vectorului, apoi suma acestor vectori este vectorul de închidere , al cărui început coincide cu începutul primului vector și al cărui sfârșit coincide cu sfârșitul ultimului vector . (Fig. 4)

Termenii se numesc componente ale vectorului, iar regula formulată este regula poligonului. Este posibil ca acest poligon să nu fie plat.

Când un vector este înmulțit cu numărul -1, se obține vectorul opus. Vectorii și au aceeași lungime și direcții opuse. Suma lor dă vector nul, a cărui lungime este zero. Direcția vectorului nul nu este definită.

În algebra vectorială, nu este nevoie să se ia în considerare separat operația de scădere: a scădea un vector dintr-un vector înseamnă a adăuga vectorul opus la vector, i.e.

Exemplul 1 Simplificați expresia:

adică vectorii pot fi adunați și înmulțiți cu numere în același mod ca polinoamele (în special, de asemenea, probleme pentru simplificarea expresiilor). De obicei, necesitatea de a simplifica expresii similare liniar cu vectori apare înainte de a calcula produsele vectorilor.

Exemplul 2 Vectorii și servesc drept diagonale ale paralelogramului ABCD (Fig. 4a). Exprimați în termeni de și vectorii , , și , care sunt laturile acestui paralelogram.

Soluţie. Punctul de intersecție al diagonalelor unui paralelogram bisectează fiecare diagonală. Lungimile vectorilor solicitați în starea problemei se găsesc fie ca jumătate din sumele vectorilor care formează un triunghi cu cei doriti, fie ca jumătate din diferențe (în funcție de direcția vectorului care servește drept diagonală), sau, ca și în ultimul caz, jumătate din suma luată cu semnul minus. Rezultatul sunt vectorii necesari în starea problemei:

Există toate motivele să credem că acum ați răspuns corect la întrebarea despre vectorii „Întreprindere” și „Abilități inovatoare” de la începutul acestei lecții. Răspuns corect: acești vectori sunt supuși unei operații de adunare.

Rezolvați singur problemele pe vectori, apoi uitați-vă la soluții

Cum se află lungimea sumei vectorilor?

Această problemă ocupă un loc aparte în operațiile cu vectori, deoarece implică utilizarea proprietăților trigonometrice. Să presupunem că aveți o sarcină ca următoarea:

Având în vedere lungimea vectorilor iar lungimea sumei acestor vectori . Aflați lungimea diferenței acestor vectori.

Soluții la aceasta și alte probleme similare și explicații despre cum să le rezolvi - în lecția " Adunarea vectorială: lungimea sumei vectorilor și teorema cosinusului ".

Și puteți verifica soluția unor astfel de probleme pe Calculator online „Latura necunoscută a unui triunghi (adunare vectorială și teorema cosinusului)” .

Unde sunt produsele vectorilor?

Produsele unui vector de la un vector nu sunt operații liniare și sunt considerate separat. Și avem lecții „Produsul punctual al vectorilor” și „Produsul vectorial și mixt al vectorilor”.

Proiecția unui vector pe o axă

Proiecția unui vector pe o axă este egală cu produsul dintre lungimea vectorului proiectat și cosinusul unghiului dintre vector și axă:

După cum se știe, proiecția unui punct A pe linie (plan) este baza perpendicularei coborâte din acest punct la dreapta (plan).

Fie - un vector arbitrar (Fig. 5) și și - proiecții ale începutului său (puncte A) și sfârșit (puncte B) pe axă l. (Pentru a construi proiecția unui punct A) trage direct prin punct A plan perpendicular pe dreapta. Intersecția unei linii și a unui plan va determina proiecția necesară.

Componentă a vectorului pe axa l numit un astfel de vector situat pe această axă, începutul căruia coincide cu proiecția începutului, iar sfârșitul - cu proiecția sfârșitului vectorului.

Proiecția vectorului pe axă l numit un număr

egală cu lungimea vectorului component pe această axă, luată cu semnul plus dacă direcția componentei coincide cu direcția axei l, și cu semnul minus dacă aceste direcții sunt opuse.

Principalele proprietăți ale proiecțiilor vectoriale pe axă:

1. Proiecțiile vectorilor egali pe aceeași axă sunt egale între ele.

2. Când un vector este înmulțit cu un număr, proiecția lui este înmulțită cu același număr.

3. Proiecția sumei vectorilor pe orice axă este egală cu suma proiecțiilor pe aceeași axă a termenilor vectorilor.

4. Proiecția unui vector pe o axă este egală cu produsul dintre lungimea vectorului proiectat și cosinusul unghiului dintre vector și axă:

Soluţie. Să proiectăm vectorii pe axă l așa cum este definit în referința teoretică de mai sus. Din Fig.5a este evident că proiecția sumei vectorilor este egală cu suma proiecțiilor vectorilor. Calculăm aceste proiecții:

Găsim proiecția finală a sumei vectorilor:

Relația unui vector cu un sistem de coordonate carteziene dreptunghiulare în spațiu

Cunoștință cu Sistemul de coordonate carteziene dreptunghiulare în spațiu a avut loc în lecția corespunzătoare, de preferință deschideți-l într-o fereastră nouă.

Într-un sistem ordonat de axe de coordonate 0xyz axă Bou numit axa x, axa 0y – axa y, și axa 0z – aplica axa.

cu punct arbitrar M vector de legătură spațială

numit vector rază puncte Mși proiectați-l pe fiecare dintre axele de coordonate. Să notăm valorile proiecțiilor corespunzătoare:

Numerele x, y, z numit coordonatele punctului M, respectiv abscisă, ordonatăȘi aplicatie, și sunt scrise ca un punct ordonat de numere: M(x; y; z)(Fig. 6).

Se numește un vector de unitate de lungime a cărui direcție coincide cu direcția axei vector unitar(sau ortom) topoare. Notează prin

În consecință, vectorii unitari ai axelor de coordonate Bou, Oi, Oz

Teorema. Orice vector poate fi descompus în vectorii unitari ai axelor de coordonate:

(2)

Egalitatea (2) se numește expansiunea vectorului de-a lungul axelor de coordonate. Coeficienții acestei expansiuni sunt proiecțiile vectorului pe axele de coordonate. Astfel, coeficienții de expansiune (2) ai vectorului de-a lungul axelor de coordonate sunt coordonatele vectorului.

După alegerea unui anumit sistem de coordonate în spațiu, vectorul și triplul coordonatelor sale se determină în mod unic unul pe celălalt, astfel încât vectorul poate fi scris sub forma

Reprezentările vectoriale în forma (2) și (3) sunt identice.

Condiția vectorilor coliniari în coordonate

După cum am observat deja, vectorii sunt numiți coliniari dacă sunt legați prin relație

Să vectori . Acești vectori sunt coliniari dacă coordonatele vectorilor sunt legate prin relație

adică coordonatele vectorilor sunt proporţionale.

Exemplul 6 Vectori dați . Acești vectori sunt coliniari?

Soluţie. Să aflăm raportul dintre coordonatele acestor vectori:

Coordonatele vectorilor sunt proporționale, prin urmare, vectorii sunt coliniari sau, ceea ce este același, paraleli.

Lungimea vectorului și cosinusurile de direcție

Datorită perpendicularității reciproce a axelor de coordonate, lungimea vectorului

egală cu lungimea diagonalei cuboid, construit pe vectori

și se exprimă prin egalitate

(4)

Un vector este complet definit prin specificarea a două puncte (început și sfârșit), astfel încât coordonatele vectorului pot fi exprimate în termeni de coordonatele acestor puncte.

Fie începutul vectorului în sistemul de coordonate dat să fie în punctul

iar sfârșitul este la punct

Din egalitate

Urmează asta

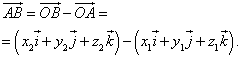
sau sub formă de coordonate

Prin urmare, coordonatele vectorului sunt egale cu diferențele dintre coordonatele cu același nume ale sfârșitului și începutului vectorului . Formula (4) în acest caz ia forma

Se determină direcția vectorului cosinus de direcție . Acestea sunt cosinusurile unghiurilor pe care le face vectorul cu axele Bou, OiȘi Oz. Să desemnăm, respectiv, aceste unghiuri α , β Și γ . Atunci cosinusurile acestor unghiuri pot fi găsite prin formule

Cosinusurile de direcție ale unui vector sunt, de asemenea, coordonatele vectorului vectorului și, prin urmare, vectorului vectorului

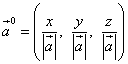
Având în vedere că lungimea vectorului vector este egală cu o unitate, adică

obținem următoarea egalitate pentru cosinusurile direcției:

Exemplul 7 Aflați lungimea unui vector X = (3; 0; 4).

Soluţie. Lungimea vectorului este

Exemplul 8 Puncte date:

Aflați dacă triunghiul construit pe aceste puncte este isoscel.

Soluţie. Folosind formula de lungime vectorială (6), găsim lungimile laturilor și aflăm dacă sunt două dintre ele egale:

Au fost găsite două laturi egale, deci nu este nevoie să căutați lungimea celei de-a treia laturi, iar triunghiul dat este isoscel.

Exemplul 9 Aflați lungimea unui vector și cosinusurile direcției acestuia dacă .

Soluţie. Coordonatele vectoriale sunt date:

Lungimea vectorului este egală cu rădăcina pătrată a sumei pătratelor coordonatelor vectorului:

Găsirea cosinusurilor direcției:

Rezolvați singur problema pe vectori și apoi uitați-vă la soluție

Operații pe vectori dați sub formă de coordonate

Fie doi vectori și dați de proiecțiile lor:

Să indicăm acțiunile asupra acestor vectori.

În cele din urmă, am pus mâna pe un subiect amplu și mult așteptat geometrie analitică. În primul rând, puțin despre această secțiune de matematică superioară... Cu siguranță că acum ți-ai amintit cursul de geometrie școlară cu numeroase teoreme, dovezile lor, desene etc. Ce să ascunzi, un subiect neiubit și adesea obscur pentru o proporție semnificativă de studenți. Geometria analitică, destul de ciudat, poate părea mai interesantă și mai accesibilă. Ce înseamnă adjectivul „analitic”? Imediat îmi vin în minte două întorsături matematice ștampilate: „metoda grafică de soluție” și „metoda analitică de soluție”. Metoda grafică, desigur, este asociat cu construcția de grafice, desene. Analitic la fel metodă presupune rezolvarea problemelor predominant prin operatii algebrice. În acest sens, algoritmul pentru rezolvarea aproape a tuturor problemelor de geometrie analitică este simplu și transparent, de multe ori este suficient să aplicați cu exactitate formulele necesare - iar răspunsul este gata! Nu, desigur, nu se va lipsi deloc de desene, în plus, pentru o mai bună înțelegere a materialului, voi încerca să le aduc peste nevoie.

Cursul deschis de lecții de geometrie nu pretinde a fi complet teoretic, este axat pe rezolvarea problemelor practice. Voi include în prelegerile mele doar ceea ce, din punctul meu de vedere, este important din punct de vedere practic. Dacă aveți nevoie de o referință mai completă la orice subsecțiune, vă recomand următoarea literatură destul de accesibilă:

1) Un lucru care, fără glumă, este familiar mai multor generații: Manual școlar de geometrie, autorii - L.S. Atanasyan și Compania. Acest cuier al vestiarului școlii a rezistat deja la 20 (!) reeditări, ceea ce, desigur, nu este limita.

2) Geometrie în 2 volume. Autorii L.S. Atanasyan, Bazylev V.T.. Aceasta este literatura pentru liceu, vei avea nevoie primul volum. Sarcinile care apar rar pot cădea în afara câmpului meu vizual și tutorial va oferi un ajutor neprețuit.

Ambele cărți pot fi descărcate gratuit online. În plus, puteți folosi arhiva mea cu soluții gata făcute, care se găsesc pe pagină Descărcați exemple de matematică superioară .

Dintre instrumente, ofer din nou propria mea dezvoltare - pachete software pe geometria analitică, care va simplifica foarte mult viața și va economisi mult timp.

Se presupune că cititorul este familiarizat cu conceptele și figurile geometrice de bază: punct, dreaptă, plan, triunghi, paralelogram, paralelipiped, cub etc. Este indicat să vă amintiți unele teoreme, cel puțin teorema lui Pitagora, salut repetitoare)

Și acum vom lua în considerare secvențial: conceptul de vector, acțiuni cu vectori, coordonate vectoriale. Mai departe recomand lectura cel mai important articol Produsul punctual al vectorilor , precum și Vector și produsul mixt al vectorilor . O sarcină locală nu va fi de prisos - Divizarea segmentului în acest sens. Pe baza informațiilor de mai sus, puteți ecuația unei drepte într-un plan din cele mai simple exemple de soluții , ceea ce va permite învață cum să rezolvi probleme de geometrie . Următoarele articole sunt de asemenea utile: Ecuația unui plan în spațiu , Ecuațiile unei linii drepte în spațiu , Sarcini de bază pe o linie dreaptă și un plan, alte ramuri ale geometriei analitice. Desigur, sarcinile standard vor fi luate în considerare pe parcurs.

Conceptul de vector. vector liber

Mai întâi, să repetăm definiția școlară a unui vector. Vector numit regizat un segment pentru care sunt indicate începutul și sfârșitul:

În acest caz, începutul segmentului este punctul , sfârșitul segmentului este punctul . Vectorul însuși este notat cu . Direcţie este esențial, dacă rearanjați săgeata la celălalt capăt al segmentului, obțineți un vector și acesta este deja vector complet diferit. Este convenabil să identifici conceptul de vector cu mișcarea unui corp fizic: trebuie să recunoști că intrarea pe ușile unui institut sau părăsirea ușilor unui institut sunt lucruri complet diferite.

Este convenabil să luați în considerare punctele individuale ale unui plan, spațiul așa-numitul vector zero. Un astfel de vector are același capăt și același început.

!!! Notă: Aici și mai jos, puteți presupune că vectorii se află în același plan sau puteți presupune că sunt localizați în spațiu - esența materialului prezentat este valabilă atât pentru plan, cât și pentru spațiu.

Denumiri: Mulți au atras imediat atenția asupra unui băț fără săgeată în denumire și au spus că au pus și o săgeată în vârf! Așa e, poți scrie cu o săgeată: , dar admisibil și înregistrare pe care o voi folosi mai târziu. De ce? Aparent, un astfel de obicei s-a dezvoltat din considerente practice, împușcătorii mei de la școală și universitate s-au dovedit a fi prea diverși și plini. În literatura educațională, uneori nu se deranjează deloc cu cuneiformul, ci evidențiază literele cu caractere aldine: , implicând astfel că acesta este un vector.

Acesta a fost stilul și acum despre modalitățile de scriere a vectorilor:

1) Vectorii se pot scrie cu două litere mari latine:
etc. În timp ce prima literă neapărat indică punctul de început al vectorului, iar a doua literă indică punctul final al vectorului.

2) Vectorii se scriu și cu litere mici latine:
În special, vectorul nostru poate fi redesemnat pentru concizie printr-o literă latină mică.

Lungime sau modul vectorul diferit de zero se numește lungimea segmentului. Lungimea vectorului nul este zero. Logic.

Lungimea unui vector se notează prin semnul modulo: ,

Cum să găsim lungimea unui vector, vom învăța (sau vom repeta, pentru cine cum) puțin mai târziu.

Era o informație elementară despre vector, familiară tuturor școlarilor. În geometria analitică, așa-numita vector liber.

Dacă e destul de simplu - vectorul poate fi desenat din orice punct:

Obișnuiam să numim astfel de vectori egali (definiția vectorilor egali va fi dată mai jos), dar din punct de vedere pur matematic, acesta este ACEȘI VECTOR sau vector liber. De ce gratuit? Pentru că în cursul rezolvării problemelor puteți „atașa” unul sau altul vector „școală” la ORICE punct al planului sau spațiului de care aveți nevoie. Aceasta este o proprietate foarte cool! Imaginați-vă un segment direcționat de lungime și direcție arbitrară - poate fi „clonat” de un număr infinit de ori și în orice punct al spațiului, de fapt, există ORIUNDE. Există un astfel de proverb al elevului: Fiecare lector în f ** u în vector. La urma urmei, nu este doar o rimă plină de duh, totul este aproape corect - un segment regizat poate fi atașat și acolo. Dar nu vă grăbiți să vă bucurați, elevii înșiși suferă mai des =)

Asa de, vector liber- acest Multe segmente direcţionale identice. Definiția școlară a unui vector, dată la începutul paragrafului: „Un segment direcționat se numește vector...”, implică specific un segment direcționat luat dintr-o mulțime dată, care este atașat unui anumit punct din plan sau spațiu.

De remarcat că din punct de vedere al fizicii, conceptul de vector liber este în general incorect, iar punctul de aplicare contează. Într-adevăr, o lovitură directă cu aceeași forță pe nas sau pe frunte este suficientă pentru a dezvolta exemplul meu stupid atrage consecințe diferite. In orice caz, nu este gratis vectori întâlniși în cursul vyshmat (nu mergeți acolo :)).

Acțiuni cu vectori. Coliniaritatea vectorilor

ÎN curs şcolar geometria ia în considerare o serie de acțiuni și reguli cu vectori: adunarea după regula triunghiului, adunarea după regula paralelogramului, regula diferenței vectorilor, înmulțirea unui vector cu un număr, produsul scalar al vectorilor etc. Ca sămânță, repetăm două reguli care sunt deosebit de relevante pentru rezolvarea problemelor de geometrie analitică.

Regula adunării vectorilor după regula triunghiurilor

Luați în considerare doi vectori arbitrari nenuli și:

Este necesar să se găsească suma acestor vectori. Datorită faptului că toți vectorii sunt considerați liberi, amânăm vectorul de la Sfârșit vector:

Suma vectorilor este vectorul. Pentru o mai bună înțelegere a regulii, este recomandabil să îi puneți un sens fizic: lăsați un corp să facă o cale de-a lungul vectorului și apoi de-a lungul vectorului. Atunci suma vectorilor este vectorul drumului rezultat care începe în punctul de plecare și se termină în punctul de sosire. O regulă similară este formulată pentru suma oricărui număr de vectori. După cum se spune, corpul își poate merge puternic în zig-zag, sau poate pe pilot automat - de-a lungul vectorului sumă rezultat.

Apropo, dacă vectorul este amânat de la start vector , atunci obținem echivalentul regula paralelogramului adaos de vectori.

În primul rând, despre coliniaritatea vectorilor. Cei doi vectori se numesc coliniare dacă se află pe aceeaşi linie sau pe drepte paralele. În linii mari, vorbim despre vectori paraleli. Dar în raport cu ele, se folosește întotdeauna adjectivul „coliniar”.

Imaginează-ți doi vectori coliniari. Dacă săgețile acestor vectori sunt îndreptate în aceeași direcție, atunci se numesc astfel de vectori co-directional. Dacă săgețile arată în direcții diferite, atunci vectorii vor fi îndreptat opus.

Denumiri: coliniaritatea vectorilor este scrisă cu pictograma obișnuită de paralelism: , în timp ce detalierea este posibilă: (vectorii sunt co-direcționați) sau (vectorii sunt direcționați opus).

muncă a unui vector diferit de zero printr-un număr este un vector a cărui lungime este egală cu , iar vectorii și sunt co-direcționați către și direcționați opus către .

Regula pentru înmulțirea unui vector cu un număr este mai ușor de înțeles cu o imagine:

Înțelegem mai detaliat:

1) Direcția. Dacă multiplicatorul este negativ, atunci vectorul schimbă direcția spre opus.

2) Lungimea. Dacă factorul este conținut în sau , atunci lungimea vectorului scade. Deci, lungimea vectorului este de două ori mai mică decât lungimea vectorului. Dacă multiplicatorul modulo este mai mare decât unu, atunci lungimea vectorului crește la timp.

3) Vă rugăm să rețineți că toți vectorii sunt coliniari, în timp ce un vector este exprimat prin altul, de exemplu, . Este adevărat și invers: dacă un vector poate fi exprimat în termenii altuia, atunci astfel de vectori sunt în mod necesar coliniari. În acest fel: dacă înmulțim un vector cu un număr, obținem coliniari(față de original) vector.

4) Vectorii sunt codirectionali. Vectorii și sunt, de asemenea, codirecționali. Orice vector al primului grup este opus oricărui vector al celui de-al doilea grup.

Ce vectori sunt egali?

Doi vectori sunt egali daca sunt codirectionali si au aceeasi lungime. Rețineți că co-direcția implică faptul că vectorii sunt coliniari. Definiția va fi inexactă (redundantă) dacă spuneți: „Doi vectori sunt egali dacă sunt coliniari, co-direcționați și au aceeași lungime”.

Din punctul de vedere al conceptului de vector liber, vectori egali este același vector ca cel discutat în paragraful anterior.

Coordonate vectoriale în plan și în spațiu

Primul punct este să luăm în considerare vectorii pe un plan. Desenați un sistem de coordonate dreptunghiular cartezian și lăsați-l deoparte de origine singur vectori și:

Vectori și ortogonală. Ortogonal = Perpendicular. Vă recomand să vă obișnuiți încet cu termenii: în loc de paralelism și perpendicularitate, folosim cuvintele respectiv coliniaritateȘi ortogonalitatea.

Desemnare: ortogonalitatea vectorilor se scrie cu semnul perpendicular obișnuit, de exemplu: .

Vectorii considerați sunt numiți vectori de coordonate sau orts. Acești vectori se formează bază la suprafata. Care este baza, cred, este intuitiv clar pentru mulți, informații mai detaliate pot fi găsite în articol Dependența liniară (non) a vectorilor. Baza vectorială .În cuvinte simple, baza și originea coordonatelor definesc întregul sistem - acesta este un fel de fundație pe care fierbe o viață geometrică plină și bogată.

Uneori se numește baza construită ortonormal baza planului: „orto” - deoarece vectorii de coordonate sunt ortogonali, adjectivul „normalizat” înseamnă unitate, i.e. lungimile vectorilor de bază sunt egale cu unu.

Desemnare: baza este de obicei scrisă între paranteze, în interiorul cărora în ordine strictă vectorii de bază sunt listați, de exemplu: . Vectori de coordonate este interzis schimba locurile.

Orice vector plan singura cale exprimat ca:
, Unde - numerele, care se numesc coordonate vectorialeîn această bază. Dar expresia în sine numit descompunere vectorialăbază .

Cina servita:

Să începem cu prima literă a alfabetului: . Desenul arată clar că atunci când se descompune vectorul din punct de vedere al bazei, se folosesc cele luate în considerare:
1) regula înmulțirii unui vector cu un număr: și ;
2) adunarea vectorilor după regula triunghiului: .

Acum lăsați mental deoparte vectorul din orice alt punct al planului. Este destul de evident că corupția lui îl va „urma neîncetat”. Iată, libertatea vectorului - vectorul „poartă totul cu tine”. Această proprietate, desigur, este adevărată pentru orice vector. Este amuzant că vectorii de bază (liberi) în sine nu trebuie să fie puși deoparte de origine, unul poate fi desenat, de exemplu, în stânga jos, iar celălalt în dreapta sus, și nimic nu se va schimba! Adevărat, nu trebuie să faceți acest lucru, deoarece profesorul va arăta, de asemenea, originalitate și vă va trage un „permis” într-un loc neașteptat.

Vectori , ilustrează exact regula de înmulțire a unui vector cu un număr, vectorul este co-direcționat cu vectorul de bază, vectorul este direcționat opus vectorului de bază. Pentru acești vectori, una dintre coordonate este egală cu zero, poate fi scrisă meticulos după cum urmează:

Și vectorii de bază, apropo, sunt așa: (de fapt, ei sunt exprimați prin ei înșiși).

Și, în sfârșit: , . Apropo, ce este scăderea vectorială și de ce nu ți-am spus despre regula scăderii? Undeva în algebra liniară, nu-mi amintesc unde, am observat că scăderea este un caz special de adunare. Deci, expansiunile vectorilor „de” și „e” sunt scrise calm ca o sumă: . Urmăriți desenul pentru a vedea cât de bine funcționează adunarea veche a vectorilor conform regulii triunghiului în aceste situații.

Considerată descompunerea formei numită uneori descompunere vectorială în sistem ort(adică în sistemul de vectori unitari). Dar aceasta nu este singura modalitate de a scrie un vector, următoarea opțiune este comună:

Sau cu semnul egal:

Vectorii de bază înșiși sunt scriși după cum urmează: și

Adică, coordonatele vectorului sunt indicate în paranteze. ÎN sarcini practice Sunt utilizate toate cele trei opțiuni.

Mă îndoiam dacă să vorbesc, dar totuși voi spune: coordonatele vectoriale nu pot fi rearanjate. Strict pe primul loc notează coordonatele care corespund vectorului unitar, strict pe locul doi notează coordonata care corespunde vectorului unitar . Într-adevăr, și sunt doi vectori diferiți.

Ne-am dat seama de coordonatele din avion. Acum luați în considerare vectorii din spațiul tridimensional, totul este aproape la fel aici! Va fi adăugată doar o singură coordonată. Este dificil de realizat desene tridimensionale, așa că mă voi limita la un vector, pe care pentru simplitate îl voi amâna de la origine:

Orice vector spațial 3d singura cale se extinde pe o bază ortonormală:
, unde sunt coordonatele vectorului (numărului) în baza dată.

Exemplu din imagine: . Să vedem cum funcționează aici regulile de acțiune vectorială. În primul rând, înmulțind un vector cu un număr: (săgeată roșie), (săgeată verde) și (săgeată magenta). În al doilea rând, iată un exemplu de adăugare a mai multor, în acest caz trei, vectori: . Vectorul sumă începe la punctul de plecare (începutul vectorului) și se termină în punctul final de sosire (sfârșitul vectorului).

Toți vectorii spațiului tridimensional, desigur, sunt și ei liberi, încercați să amânați mental vectorul din orice alt punct și veți înțelege că expansiunea lui „rămâne cu el”.

Similar cu cazul avionului, pe lângă scris versiunile cu paranteze sunt utilizate pe scară largă: fie .

Dacă unul (sau doi) vectori de coordonate lipsesc în expansiune, atunci se pun zerouri. Exemple:
vector (minuțios ) - scrie ;
vector (minuțios) - notează;
vector (minuțios ) - scrie .

Vectorii de bază se scriu după cum urmează:

Aici, poate, sunt toate cunoștințele teoretice minime necesare pentru a rezolva probleme de geometrie analitică. Poate că există prea mulți termeni și definiții, așa că recomand manechine pentru a reciti și a înțelege aceasta informatie din nou. Și va fi util oricărui cititor să se refere din când în când la lecția de bază pentru o mai bună asimilare a materialului. Coliniaritate, ortogonalitate, bază ortonormală, descompunere vectorială - acestea și alte concepte vor fi adesea folosite în cele ce urmează. Remarc că materialele site-ului nu sunt suficiente pentru a trece un test teoretic, un colocviu de geometrie, din moment ce criptez cu grijă toate teoremele (în afară de fără dovezi) - în detrimentul stilului științific de prezentare, dar un plus pentru înțelegerea dvs. a subiectului. Pentru a primi informații teoretice detaliate, vă rog să vă înclinați în fața profesorului Atanasyan.

Acum să trecem la partea practică:

Cele mai simple probleme de geometrie analitică.
Acțiuni cu vectori în coordonate

Sarcinile care vor fi luate în considerare, este foarte de dorit să învățați cum să le rezolvați complet automat și formulele memora, nici nu-l amintesc intenționat, își vor aminti ei înșiși =) Acest lucru este foarte important, deoarece alte probleme de geometrie analitică se bazează pe cele mai simple exemple elementare și va fi enervant să petreci timp suplimentar mâncând pioni. Nu trebuie să-ți închizi nasturii de sus pe cămașă, multe lucruri îți sunt familiare de la școală.

Prezentarea materialului va urma un curs paralel - atât pentru avion, cât și pentru spațiu. Din motivul că toate formulele... veți vedea singur.

Cum să găsiți un vector având două puncte?

Dacă sunt date două puncte ale planului și, atunci vectorul are următoarele coordonate:

Dacă sunt date două puncte în spațiu și, atunci vectorul are următoarele coordonate:

adica de la coordonatele capătului vectorului trebuie să scazi coordonatele corespunzătoare pornire vectorială.

Sarcina: Pentru aceleași puncte, scrieți formulele pentru găsirea coordonatelor vectorului. Formule la sfârșitul lecției.

Exemplul 1

Având în vedere două puncte în plan și . Găsiți coordonatele vectoriale

Soluţie: după formula corespunzătoare:

În mod alternativ, se poate folosi următoarea notație:

Esteții vor decide astfel:

Personal, m-am obișnuit cu prima versiune a discului.

Răspuns:

Conform condiției, nu a fost necesar să se construiască un desen (ceea ce este tipic pentru problemele de geometrie analitică), dar pentru a explica unele puncte manechinilor, nu voi fi prea leneș:

Trebuie inteles diferența dintre coordonatele punctului și coordonatele vectoriale:

Coordonatele punctului sunt coordonatele obișnuite într-un sistem de coordonate dreptunghiular. Pune deoparte puncte pentru plan de coordonate Cred că toată lumea o poate face din clasa 5-6. Fiecare punct are un loc strict în avion și nu pot fi mutați nicăieri.

Coordonatele aceluiasi vector este extinderea sa în raport cu baza , în acest caz . Orice vector este liber, prin urmare, dacă se dorește sau este necesar, îl putem amâna cu ușurință dintr-un alt punct din plan. Interesant, pentru vectori, nu puteți construi deloc axe, un sistem de coordonate dreptunghiular, aveți nevoie doar de o bază, în acest caz, de o bază ortonormală a planului.

Înregistrările coordonatelor punctului și ale coordonatelor vectoriale par a fi similare: , și simțul coordonatelor absolut diferit, și ar trebui să fiți bine conștienți de această diferență. Această diferență, desigur, este valabilă și pentru spațiu.

Doamnelor și domnilor, ne umplem mâinile:

Exemplul 2

a) Punctele date și . Găsiți vectori și .
b) Se acordă puncte Și . Găsiți vectori și .
c) Punctele date și . Găsiți vectori și .
d) Se acordă puncte. Găsiți Vectori .

Poate suficient. Acestea sunt exemple pentru o decizie independentă, încearcă să nu le neglijezi, va da roade ;-). Desenele nu sunt necesare. Soluții și răspunsuri la sfârșitul lecției.

Ce este important în rezolvarea problemelor de geometrie analitică? Este important să fii EXTREM DE ATENȚIE pentru a evita eroarea magistrală „doi plus doi egal zero”. Îmi cer scuze anticipat dacă am greșit =)

Cum se află lungimea unui segment?

Lungimea, așa cum sa menționat deja, este indicată de semnul modulului.

Dacă sunt date două puncte ale planului și, atunci lungimea segmentului poate fi calculată prin formula

Dacă sunt date două puncte în spațiu și, atunci lungimea segmentului poate fi calculată prin formula

Notă: Formulele vor rămâne corecte dacă coordonatele corespunzătoare sunt schimbate: și , dar prima opțiune este mai standard

Exemplul 3

Soluţie: după formula corespunzătoare:

Răspuns:

Pentru claritate, voi face un desen

Secțiune - nu este un vector, și nu o poți muta nicăieri, desigur. În plus, dacă completați desenul la scară: 1 unitate. \u003d 1 cm (două celule tetrade), atunci răspunsul poate fi verificat cu o riglă obișnuită, măsurând direct lungimea segmentului.

Da, soluția este scurtă, dar există câteva puncte importante pe care aș dori să le clarific:

În primul rând, în răspuns am stabilit dimensiunea: „unități”. Condiția nu spune CE este, milimetri, centimetri, metri sau kilometri. Prin urmare, formularea generală va fi o soluție competentă din punct de vedere matematic: „unități” - abreviat ca „unități”.

În al doilea rând, să repetăm materialul școlar, care este util nu numai pentru problema luată în considerare:

fi atent la truc tehnic important – scotând multiplicatorul de sub rădăcină. Ca rezultat al calculelor, am obținut rezultatul și un stil matematic bun implică scoaterea factorului de sub rădăcină (dacă este posibil). Procesul arată astfel mai detaliat: . Bineînțeles, lăsarea răspunsului în formă nu va fi o greșeală - dar este cu siguranță un defect și un argument serios pentru stricaciune din partea profesorului.

Iată și alte cazuri comune:

Adesea sub rădăcină se dovedește suficient număr mare, de exemplu . Cum să fii în astfel de cazuri? Pe calculator, verificăm dacă numărul este divizibil cu 4:. Da, împărțiți complet, astfel: . Sau poate numărul poate fi împărțit din nou la 4? . În acest fel: . Ultima cifră a numărului este impară, deci împărțirea la 4 pentru a treia oară nu este în mod clar posibilă. Încercarea de a împărți la nouă: . Ca rezultat:
Gata.

Ieșire: dacă sub rădăcină obținem un număr întreg care nu poate fi extras, atunci încercăm să scoatem factorul de sub rădăcină - pe calculator verificăm dacă numărul este divizibil cu: 4, 9, 16, 25, 36, 49 , etc.

În cursul rezolvării diverselor probleme se găsesc adesea rădăcini, încercați întotdeauna să extrageți factori de sub rădăcină pentru a evita un scor mai mic și probleme inutile la finalizarea soluțiilor conform observației profesorului.

Să repetăm în același timp pătrarea rădăcinilor și a altor puteri:

Regulile pentru acțiunile cu grade în formă generală se găsesc într-un manual școlar de algebră, dar cred că totul sau aproape totul este deja clar din exemplele date.

Sarcina pentru o soluție independentă cu un segment în spațiu:

Exemplul 4

Puncte date și . Aflați lungimea segmentului.

Soluție și răspuns la sfârșitul lecției.