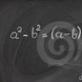Acasă » V.V. Apicultor » Calculator curbiliniu pentru suprafața trapezoidală. Calculați aria exemplelor de figuri. Deci, sistematizăm punctele importante ale acestei sarcini.

Calculator curbiliniu pentru suprafața trapezoidală. Calculați aria exemplelor de figuri. Deci, sistematizăm punctele importante ale acestei sarcini.

Începem să luăm în considerare procesul real de calcul al integralei duble și să ne familiarizăm cu semnificația ei geometrică.

Integrala dublă este numeric egală cu aria unei figuri plate (regiunea de integrare). Aceasta este cea mai simplă formă a integralei duble, când funcția a două variabile este egală cu una: .

Să luăm mai întâi în considerare problema în termeni generali. Acum vei fi surprins cât de simplu este cu adevărat! Să calculăm aria unei figuri plate delimitate de linii. Pentru certitudine, presupunem că pe intervalul . Aria acestei figuri este numeric egală cu:

Să descriem zona din desen:

Să alegem prima modalitate de a ocoli zona:

Prin urmare:

Și imediat un truc tehnic important: integralele iterate pot fi considerate separat. Mai întâi integrala interioară, apoi integrala exterioară. Această metodă este foarte recomandată pentru începătorii în tema ceainicelor.

1) Calculați integrala internă, în timp ce integrarea se realizează peste variabila „y”:

Integrala nedefinită aici este cea mai simplă, iar apoi se folosește formula banală Newton-Leibniz, cu singura diferență că limitele integrării nu sunt numerele, ci funcțiile. În primul rând, am înlocuit limita superioară în „y” (funcția antiderivată), apoi limita inferioară

2) Rezultatul obţinut la primul paragraf trebuie înlocuit în integrala externă:

O notație mai compactă pentru întreaga soluție arată astfel:

Formula rezultată este exact formula de lucru pentru calcularea ariei unei figuri plate folosind integrala definită „obișnuită”! Vezi lecția Calcularea ariei folosind o integrală definită, acolo este ea la fiecare pas!

Acesta este, problema calculării ariei folosind o integrală dublă putin diferit din problema găsirii zonei folosind o integrală definită! De fapt, sunt una și aceeași!

Prin urmare, nu ar trebui să apară dificultăți! Nu voi lua în considerare foarte multe exemple, deoarece, de fapt, ați întâmpinat această problemă în mod repetat.

Exemplul 9

Soluţie: Să descriem zona din desen:

Să alegem următoarea ordine de parcurgere a regiunii:

Aici și mai jos, nu voi intra în modul de a traversa o zonă pentru că primul paragraf a fost foarte detaliat.

Prin urmare:

După cum am menționat deja, este mai bine pentru începători să calculeze integrale iterate separat, voi adera la aceeași metodă:

1) În primul rând, folosind formula Newton-Leibniz, ne ocupăm de integrala internă:

2) Rezultatul obținut la prima etapă este înlocuit în integrala exterioară:

Punctul 2 este de fapt găsirea aria unei figuri plate folosind o integrală definită.

Răspuns:

Iată o sarcină atât de stupidă și naivă.

Un exemplu curios pentru o soluție independentă:

Exemplul 10

Folosind integrala dublă, calculați aria unei figuri plane delimitată de liniile , ,

Un exemplu de soluție finală la sfârșitul lecției.

În exemplele 9-10, este mult mai profitabil să folosiți prima modalitate de a ocoli zona, cititorii curioși, apropo, pot schimba ordinea ocolirii și pot calcula zonele în al doilea mod. Dacă nu greșești, atunci, firește, se obțin aceleași valori de suprafață.

Dar, în unele cazuri, a doua modalitate de a ocoli zona este mai eficientă și, în încheierea cursului tânărului tocilar, să ne uităm la câteva exemple pe acest subiect:

Exemplul 11

Folosind integrala dublă, calculați aria unei figuri plane delimitate de linii.

Soluţie: aşteptăm cu nerăbdare două parabole cu o briză care stau pe partea lor. Nu este nevoie să zâmbești, lucruri similare în integrale multiple sunt adesea întâlnite.

Care este cel mai simplu mod de a face un desen?

Să reprezentăm parabola ca două funcții:
- ramura superioară și - ramura inferioară.

În mod similar, reprezentăm parabola ca ramurile superioare și inferioare.

Aria figurii este calculată folosind integrala dublă conform formulei:

Ce se întâmplă dacă alegem prima modalitate de a ocoli zona? În primul rând, această zonă va trebui împărțită în două părți. Și în al doilea rând, vom observa această imagine tristă: . Integralele, desigur, nu sunt de un nivel supercomplex, dar... există o veche zicală matematică: cine este prietenos cu rădăcinile, nu are nevoie de o compensație.

Prin urmare, din neînțelegerea dată în condiție, exprimăm funcțiile inverse:

Funcțiile inverse din acest exemplu au avantajul că stabilesc imediat întreaga parabolă fără frunze, ghinde, ramuri și rădăcini.

Conform celei de-a doua metode, traversarea zonei va fi după cum urmează:

Prin urmare:

După cum se spune, simți diferența.

1) Ne ocupăm de integrala internă:

Înlocuim rezultatul în integrala exterioară:

Integrarea peste variabila „y” nu ar trebui să fie jenantă, dacă ar exista o litera „zyu” - ar fi grozav să o integrezi peste ea. Deși cine a citit al doilea paragraf al lecției Cum se calculează volumul unui corp de revoluție, nu mai simte nici cea mai mică jenă cu integrarea peste „y”.

De asemenea, acordați atenție primului pas: integrandul este par, iar segmentul de integrare este simetric față de zero. Prin urmare, segmentul poate fi înjumătățit, iar rezultatul poate fi dublat. Această tehnică este comentată în detaliu în lecție. Metode eficiente de calcul a integralei definite.

Ce să adaugi…. Toate!

Răspuns:

Pentru a vă testa tehnica de integrare, puteți încerca să calculați . Răspunsul ar trebui să fie exact același.

Exemplul 12

Folosind integrala dublă, calculați aria unei figuri plane delimitate de linii

Acesta este un exemplu de do-it-yourself. Este interesant de remarcat faptul că, dacă încercați să utilizați prima modalitate de a ocoli zona, atunci figura nu va mai fi împărțită în două, ci în trei părți! Și, în consecință, obținem trei perechi de integrale iterate. Uneori se întâmplă.

Clasa de master s-a încheiat și este timpul să trecem la nivelul de mare maestru - Cum se calculează integrala dublă? Exemple de soluții. Voi încerca să nu fiu atât de maniac în al doilea articol =)

Vă doresc succes!

Solutii si raspunsuri:

Exemplul 2:Soluţie: Desenați o zonă pe desen:

Să alegem următoarea ordine de parcurgere a regiunii:

Prin urmare:
Să trecem la funcțiile inverse:

Prin urmare:
Răspuns:

Exemplul 4:Soluţie: Să trecem la funcțiile directe:

Să executăm desenul:

Să schimbăm ordinea de parcurgere a zonei:

Răspuns:

Ordinea de traversare a zonei:

Prin urmare:

1)
2)

Răspuns:

În această lecție vom învăța cum să calculăm zone de figuri plate, care se numesc trapezoizi curbilinii .

Exemple de astfel de cifre sunt în figura de mai jos.

Pe de o parte, găsirea ariei unei figuri plate folosind o integrală definită este extrem de simplă. Vorbim despre aria figurii, care este limitată de sus de o anumită curbă, de jos - de axa absciselor ( Bou), iar în stânga și în dreapta sunt niște linii drepte. Simplitatea este că integrala definită a funcției căreia îi este dată curba și există aria unei astfel de figuri(trapez curbiliniu).

Pentru a calcula aria unei figuri, avem nevoie de:

Integrală definită a funcției care definește curba , care limitează de sus trapezul curbiliniu. Și aici vine prima nuanță semnificativă: un trapez curbiliniu poate fi limitat de o curbă nu numai de sus, ci și de jos . Cum sa actionezi in acest caz? Simplu, dar important de reținut: integrala în acest caz este luată cu semnul minus .
Limitele integrării AȘi b, pe care îl găsim din ecuațiile dreptelor care delimitează figura din stânga și dreapta: X = A , X = b, Unde AȘi b- numere.

Separat, mai multe nuanțe.

Curba care limitează trapezul curbiliniu de sus (sau de jos) trebuie să fie graficul unei funcții continue și nenegative y = f(X) .

Valorile X trebuie să aparțină segmentului [A, b] . Adică, nu sunt luate în considerare, de exemplu, linii ca o secțiune a unei ciuperci, în care piciorul se potrivește perfect în acest segment, iar capacul este mult mai lat.

Segmentele laterale pot degenera în puncte . Dacă ați văzut o astfel de figură în desen, acest lucru nu ar trebui să vă încurce, deoarece acest punct are întotdeauna propria sa valoare pe axa x. Deci totul este în ordine cu limitele integrării.

Acum puteți trece la formule și calcule. Deci zona s trapezul curbiliniu poate fi calculat prin formula

Dacă f(X) ≤ 0 (graficul funcției este situat sub axă Bou), Acea zona unui trapez curbat poate fi calculat prin formula

Există, de asemenea, cazuri când atât granițele superioare, cât și cele inferioare ale figurii sunt funcții y = f(X) Și y = φ (X) , atunci aria unei astfel de cifre este calculată prin formula

. (3)

Rezolvăm probleme împreună

Să începem cu cazurile în care aria unei figuri poate fi calculată folosind formula (1).

Exemplul 1Bou) și direct X = 1 , X = 3 .

Soluţie. Deoarece y = 1/X> 0 pe segment, atunci aria trapezului curbiliniu se găsește cu formula (1):

Exemplul 2 Găsiți aria figurii delimitată de graficul funcției , linie dreaptă X= 1 și axa x ( Bou ).

Soluţie. Rezultatul aplicării formulei (1):

Daca atunci s= 1/2; daca atunci s= 1/3 etc.

Exemplul 3 Găsiți aria figurii delimitată de graficul funcției, axa x ( Bou) și direct X = 4 .

Soluţie. Figura corespunzătoare stării problemei este un trapez curbiliniu, în care segmentul din stânga a degenerat într-un punct. Limitele de integrare sunt 0 și 4. Deoarece, conform formulei (1), găsim aria trapezului curbiliniu:

Exemplul 4 Găsiți aria figurii delimitată de liniile , , și situată în primul sfert.

Soluţie. Pentru a folosi formula (1), reprezentăm aria figurii dată de condițiile exemplului ca suma ariilor unui triunghi OAB iar trapezul curbiliniu ABC. Când se calculează aria unui triunghi OAB limitele integrării sunt abscisele punctelor OȘi A, iar pentru figură ABC- abscisele punctelor AȘi C (A este punctul de intersecție al dreptei OAși parabole și C- punctul de intersecție al parabolei cu axa Bou). Rezolvând împreună (ca sistem) ecuațiile unei drepte și ale unei parabole, obținem (abscisa punctului A) și (abscisa altui punct de intersecție a dreptei și a parabolei, care nu este necesară pentru soluție). În mod similar, obținem , (abscise de puncte CȘi D). Acum avem totul pentru a găsi zona figurii. Găsim:

Exemplul 5 Găsiți aria unui trapez curbiliniu ACDB, dacă ecuația curbei CD si abscisa AȘi B respectiv 1 și 2.

Soluţie. Exprimăm această ecuație a curbei prin Y: aria trapezului curbiliniu se găsește prin formula (1):

Să trecem la cazurile în care aria unei figuri poate fi calculată folosind formula (2).

Exemplul 6 Găsiți aria figurii delimitată de parabolă și de axa x ( Bou ).

Soluţie. Această cifră este situată sub axa x. Prin urmare, pentru a calcula aria sa, folosim formula (2). Limitele de integrare sunt abscisele și punctele de intersecție ale parabolei cu axa Bou. Prin urmare,

Exemplul 7 Găsiți aria dintre axa x ( Bou) și două unde sinusoidale învecinate.

Soluţie. Aria acestei figuri poate fi găsită prin formula (2):

Să găsim fiecare termen separat:

În sfârșit găsim zona:

Exemplul 8 Găsiți aria figurii cuprinsă între parabolă și curbă.

Soluţie. Să exprimăm ecuațiile dreptelor în termenii lui Y:

Suprafaţa conform formulei (2) se va obţine ca

Unde AȘi b- abscisele punctelor AȘi B. Le găsim rezolvând împreună ecuațiile:

În sfârșit găsim zona:

Și, în sfârșit, există cazuri în care aria unei figuri poate fi calculată folosind formula (3).

Exemplul 9 Găsiți aria figurii cuprinsă între parabole Și .

Exemplul 1 . Calculați aria figurii mărginite de linii: x + 2y - 4 = 0, y = 0, x = -3 și x = 2

Să construim o figură (vezi fig.) Construim o linie dreaptă x + 2y - 4 \u003d 0 de-a lungul a două puncte A (4; 0) și B (0; 2). Exprimând y în termeni de x, obținem y \u003d -0,5x + 2. Conform formulei (1), unde f (x) \u003d -0,5x + 2, a \u003d -3, b \u003d 2, vom găsi

S \u003d \u003d [-0,25 \u003d 11,25 mp. unitati

Exemplul 2 Calculați aria figurii mărginite de linii: x - 2y + 4 \u003d 0, x + y - 5 \u003d 0 și y \u003d 0.

Soluţie. Să construim o figură.

Să construim o dreaptă x - 2y + 4 = 0: y = 0, x = - 4, A (-4; 0); x = 0, y = 2, B(0; 2).

Să construim o dreaptă x + y - 5 = 0: y = 0, x = 5, С(5; 0), x = 0, y = 5, D(0; 5).

Aflați punctul de intersecție al dreptelor rezolvând sistemul de ecuații:

x = 2, y = 3; M(2; 3).

Pentru a calcula aria necesară, împărțim triunghiul AMC în două triunghiuri AMN și NMC, deoarece atunci când x se schimbă de la A la N, aria este limitată de o linie dreaptă, iar când x se schimbă de la N la C, este o linie dreaptă.

Pentru triunghiul AMN avem: ; y \u003d 0,5x + 2, adică f (x) \u003d 0,5x + 2, a \u003d - 4, b \u003d 2.

Pentru triunghiul NMC avem: y = - x + 5, adică f(x) = - x + 5, a = 2, b = 5.

Calculând aria fiecărui triunghi și adunând rezultatele, găsim:

mp unitati

9 + 4, 5 = 13,5 mp. unitati Verificați: = 0,5AC = 0,5 sq. unitati

Exemplul 3 Calculați aria unei figuri mărginite de drepte: y = x 2 , y=0, x=2, x=3.

În acest caz, este necesar să se calculeze aria unui trapez curbiliniu mărginit de o parabolă y = x 2 , linii drepte x \u003d 2 și x \u003d 3 și axa Ox (a se vedea fig.) Conform formulei (1), găsim aria unui trapez curbiliniu

= = 6kv. unitati

Exemplul 4 Calculați aria unei figuri mărginite de drepte: y \u003d - x 2 + 4 și y = 0

Să construim o figură. Zona dorită este închisă între parabola y \u003d - x 2 + 4 și axa Oh.

Aflați punctele de intersecție ale parabolei cu axa x. Presupunând y \u003d 0, găsim x \u003d Deoarece această cifră este simetrică față de axa Oy, calculăm aria figurii situate în dreapta axei Oy și dublăm rezultatul: \u003d + 4x] mp. unitati 2 = 2 mp. unitati

Exemplul 5 Calculați aria unei figuri delimitate de drepte: y 2 = x, yx = 1, x = 4

Aici este necesar să se calculeze aria trapezului curbiliniu delimitată de ramura superioară a parabolei y 2 \u003d x, axa Ox și liniile drepte x \u003d 1x \u003d 4 (vezi fig.)

Conform formulei (1), unde f(x) = a = 1 și b = 4, avem = (= unități sq.

Exemplul 6 . Calculați aria figurii mărginite de drepte: y = sinx, y = 0, x = 0, x= .

Zona dorită este limitată de o sinusoidă cu jumătate de undă și de axa Ox (vezi Fig.).

Avem - cosx \u003d - cos \u003d 1 + 1 \u003d 2 metri pătrați. unitati

Exemplul 7 Calculați aria figurii mărginite de linii: y \u003d - 6x, y \u003d 0 și x \u003d 4.

Figura este situată sub axa Ox (vezi Fig.).

Prin urmare, aria sa este găsită prin formula (3)

= =

Exemplul 8 Calculați aria figurii delimitată de liniile: y \u003d și x \u003d 2. Vom construi curba y \u003d de puncte (a se vedea fig.). Astfel, aria figurii se găsește prin formula (4)

Exemplul 9 .

X 2 + y 2 = r 2 .

Aici trebuie să calculați aria delimitată de cercul x 2 + y 2 = r 2 , adică aria unui cerc de rază r centrat la origine. Să găsim a patra parte a acestei zone, luând limitele integrării de la 0

dor; avem: 1 = = [

Prin urmare, 1 =

Exemplul 10 Calculați aria figurii mărginite de linii: y \u003d x 2 și y = 2x

Această cifră este limitată de parabola y \u003d x 2 și linie dreaptă y \u003d 2x (vezi Fig.) Pentru a determina punctele de intersecție ale dreptelor date, rezolvăm sistemul de ecuații: x 2 – 2x = 0 x = 0 și x = 2

Folosind formula (5) pentru a găsi aria, obținem

= graficul funcției y = X 2 + 2 localizate peste axăBOU, De aceea:

Răspuns: .

Care are dificultăți în calcularea integralei definite și aplicarea formulei Newton-Leibniz

consultați prelegerea Integrala definita. Exemple de soluții. După ce sarcina este finalizată, este întotdeauna util să priviți desenul și să vă dați seama dacă răspunsul este real. În acest caz, „cu ochi” numărăm numărul de celule din desen - ei bine, aproximativ 9 vor fi tastate, se pare că este adevărat. Este destul de clar că dacă am avea, să zicem, răspunsul: 20 de unități pătrate, atunci, evident, s-a făcut o greșeală undeva - 20 de celule evident nu se încadrează în figura în cauză, cel mult o duzină. Dacă răspunsul s-a dovedit a fi negativ, atunci și sarcina a fost rezolvată incorect.

Exemplul 2

Calculați aria unei figuri delimitate de linii X y = 4, X = 2, X= 4 și axa BOU.

Acesta este un exemplu de do-it-yourself. Soluție completă și răspuns la sfârșitul lecției.

Ce trebuie făcut dacă este localizat trapezul curbiliniu sub axăBOU?

Exemplul 3

Calculați aria unei figuri delimitate de linii y = e-x, X= 1 și axele de coordonate.

Soluție: Să facem un desen:

Dacă un trapez curbiliniu complet sub ax BOU , atunci aria sa poate fi găsită prin formula:

În acest caz:

Atenţie! Cele două tipuri de sarcini nu trebuie confundate:

1) Dacă vi se cere să rezolvați doar o integrală definită fără nicio semnificație geometrică, atunci aceasta poate fi negativă.

2) Dacă vi se cere să găsiți aria unei figuri folosind o integrală definită, atunci aria este întotdeauna pozitivă! De aceea, în formula luată în considerare apare minusul.

În practică, cel mai adesea figura este situată atât în semiplanul superior, cât și în cel inferior și, prin urmare, de la cele mai simple probleme școlare, trecem la exemple mai semnificative.

Exemplul 4

Găsiți aria unei figuri plane delimitată de drepte y = 2X – X 2 , y = -X.

Soluție: Mai întâi trebuie să faci un desen. Când construim un desen în probleme de zonă, suntem cel mai interesați de punctele de intersecție ale liniilor. Aflați punctele de intersecție ale parabolei y = 2X – X 2 și drept y = -X. Acest lucru se poate face în două moduri. Prima modalitate este analitică. Rezolvam ecuatia:

Deci limita inferioară a integrării A= 0, limita superioară a integrării b= 3. Este adesea mai profitabil și mai rapid să construiești linii punct cu punct, în timp ce limitele integrării sunt descoperite ca „de la sine”. Cu toate acestea, metoda analitică de găsire a limitelor mai trebuie folosită uneori dacă, de exemplu, graficul este suficient de mare sau construcția filetată nu a evidențiat limitele integrării (acestea pot fi fracționale sau iraționale). Ne întoarcem la sarcina noastră: este mai rațional să construim mai întâi o linie dreaptă și abia apoi o parabolă. Hai sa facem un desen:

Repetăm că în construcția punctuală, limitele integrării sunt cel mai adesea descoperite „automat”.

Și acum formula de lucru:

Dacă pe segmentul [ A; b] oarecare funcție continuă f(X) mai mare sau egal vreo funcție continuă g(X), atunci aria figurii corespunzătoare poate fi găsită prin formula:

Aici nu mai este necesar să ne gândim unde se află figura - deasupra axei sau sub axa, dar contează ce diagramă este SUS(față de alt grafic), si care este JOS.

În exemplul luat în considerare, este evident că pe segment parabola este situată deasupra liniei drepte și, prin urmare, de la 2 X – X 2 trebuie scazut - X.

Finalizarea soluției ar putea arăta astfel:

Cifra dorită este limitată de o parabolă y = 2X – X 2 de sus și drepte y = -X de desubt.

Pe segmentul 2 X – X 2 ≥ -X. Conform formulei corespunzătoare:

Răspuns: .

De fapt, formula școlară pentru aria unui trapez curbiliniu în semiplanul inferior (a se vedea exemplul nr. 3) este un caz special al formulei

Din moment ce axa BOU este dat de ecuație y= 0 și graficul funcției g(X) este situat sub axă BOU, Acea

Și acum câteva exemple pentru o soluție independentă

Exemplul 5

Exemplul 6

Găsiți aria unei figuri delimitate de linii

În cursul rezolvării problemelor pentru calcularea ariei folosind o anumită integrală, se întâmplă uneori un incident amuzant. Desenul a fost făcut corect, calculele au fost corecte, dar, din cauza neatenției, ... a găsit zona figurii greșite.

Exemplul 7

Să desenăm mai întâi:

Figura a cărei zonă trebuie să o găsim este umbrită în albastru.(uitați-vă cu atenție la starea - cum este limitată cifra!). Dar, în practică, din cauza neatenției, ei decid adesea că trebuie să găsească zona figurii care este umbrită în verde!

Acest exemplu este, de asemenea, util prin faptul că în el aria figurii este calculată folosind două integrale definite. Într-adevăr:

1) Pe segmentul [-1; 1] deasupra axei BOU graficul este drept y = X+1;

2) Pe segmentul de deasupra axei BOU se localizează graficul hiperbolei y = (2/X).

Este destul de evident că zonele pot (și ar trebui) să fie adăugate, prin urmare:

Răspuns:

Exemplul 8

Calculați aria unei figuri delimitate de linii

Să prezentăm ecuațiile sub forma „școală”.

și faceți desenul:

Din desen se poate observa că limita noastră superioară este „bună”: b = 1.

Dar care este limita inferioară? Este clar că acesta nu este un număr întreg, dar ce?

Pot fi, A=(-1/3)? Dar unde este garanția că desenul este realizat cu acuratețe perfectă, s-ar putea dovedi că A=(-1/4). Dacă nu am înțeles deloc graficul corect?

În astfel de cazuri, trebuie să petrecem timp suplimentar și să rafinați limitele integrării analitic.

Găsiți punctele de intersecție ale graficelor

Pentru a face acest lucru, rezolvăm ecuația:

Prin urmare, A=(-1/3).

Soluția ulterioară este banală. Principalul lucru este să nu vă confundați în înlocuiri și semne. Calculele de aici nu sunt cele mai simple. Pe segment

, ,

după formula corespunzătoare:

Răspuns:

În încheierea lecției, vom considera două sarcini mai dificile.

Exemplul 9

Calculați aria unei figuri delimitate de linii

Soluție: Desenați această figură în desen.

Pentru a desena un desen punct cu punct, trebuie să cunoașteți aspectul sinusoidei. În general, este util să cunoașteți graficele tuturor funcțiilor elementare, precum și unele valori ale sinusului. Ele pot fi găsite în tabelul de valori funcții trigonometrice. În unele cazuri (de exemplu, în acest caz), este permisă construirea unui desen schematic, pe care graficele și limitele de integrare trebuie să fie afișate în principiu corect.

Nu există probleme cu limitele de integrare aici, acestea decurg direct din condiția:

- „x” se schimbă de la zero la „pi”. Luăm o altă decizie:

Pe segment, graficul funcției y= păcatul 3 X situat deasupra axei BOU, De aceea:

(1) Puteți vedea cum sinusurile și cosinusurile sunt integrate în puteri impare în lecție Integrale ale funcțiilor trigonometrice. Ciupim un sinus.

(2) Folosim identitatea trigonometrică de bază în formă